【思维】2017多校训练七 HDU6121 Build a tree

http://acm.hdu.edu.cn/showproblem.php?pid=6121

【题意】

• 询问n个结点的完全k叉树,所有子树结点个数的异或和是多少

【思路】

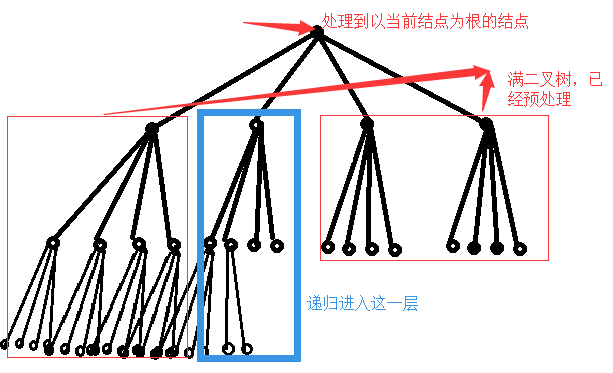
• 一棵完全K叉树，对于树的每一层，我们可以分为三种结点：

1. 满k叉树的结点
2. 不满的k叉树
3. 比第一种情况少一层的满结点的k叉树

【AC】

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 ll n,k;
 ll ans;
 ll kn[],sz[],full[];
 int cs;
 void Pre()
 {
     //kn[i]=k^i
     kn[]=;
     for(int i=;i<=cs;i++)
     {
         kn[i]=kn[i-]*k;
     }
     //根结点为第一层,sz[i]为有i层的满k叉树有多少结点
     sz[]=;
     for(int i=;i<=cs;i++)
     {
         sz[i]=sz[i-]+kn[i-];
     }
     //有i层的满k叉树所有子树结点大小的异或和
     if(k&)
     {
         full[]=;
         for(int i=;i<=cs;i++)
         {
             full[i]=full[i-]^sz[i];
         }
     }
     else
     {
         for(int i=;i<=cs;i++)
         {
             full[i]=sz[i];
         }
     }
 }
 
 void dfs(int cur)
 {
     ans^=n;
     ll lft=n-sz[cur];  //最后一层有多少个
     ll l=lft/kn[cur-];//多少个cur层的满k叉树
     lft-=l*kn[cur-];
     if(lft==)//没有不满的k叉树
     {
         if(l&) ans^=full[cur];
         if((k-l)&) ans^=full[cur-];
         return;
     }
     if(l&) ans^=full[cur];
     if((k-l-)&) ans^=full[cur-];
     n--;n-=l*sz[cur];n-=(k-l-)*sz[cur-];
     dfs(cur-);
 }
 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         ans=;
         scanf("%I64d%I64d",&n,&k);
         //k=1特判，打表看出来的
         if(k==)
         {
             if(n%==)
             {
                 ans=n;
             }
             else if(n%==)
             {
                 ans=;
             }
             else if(n%==)
             {
                 ans=n+;
             }
             else
             {
                 ans=;
             }
             printf("%I64d\n",ans);
             continue;
         }
         //根结点为第一层，结点数为n的完全k叉树有cs层是满的
         cs=;
         ll t=n;
         while(t)
         {
             t--;
             t/=k;
             cs++;
         }
         //预处理
         Pre();
         ans=;
         //递归
         dfs(cs);
         printf("%I64d\n",ans);
     }
     return ;
 }