【HDU4859】 海岸线（网络流-最小割）

Problem Description

欢迎来到珠海！

由于土地资源越来越紧张，使得许多海滨城市都只能依靠填海来扩展市区以求发展。作为Z市的决策人，在仔细观察了Z市地图之后，你准备通过填充某些海域来扩展Z市的海岸线到最长，来吸引更多的游客前来旅游度假。为了简化问题，假设地图为一个N*M的格子，其中一些是陆地，一些是可以填充的浅海域，一些是不可填充的深海域。这里定义海岸线的长度为一个联通块陆地（可能包含浅海域填充变为的陆地）的边缘长度，两个格子至少有一个公共边，则视为联通。

值得注意的是，这里Z市的陆地区域可以是不联通的，并且整个地图都处在海洋之中，也就是说，Z市是由一些孤岛组成的，比如像，夏威夷？

你的任务是，填充某些浅海域，使得所有岛屿的海岸线之和最长。

Input

输入第一行为T，表示有T组测试数据。
每组数据以两个整数N和M开始，表示地图的规模。接下来的N行，每一行包含一个长度为M的字符串，表示地图，‘.’表示陆地，’E’表示浅海域，’D’表示深海域。

[Technical Specification]

1. 1 <= T <= 100
2. 1 <= N, M <= 47

Output

对每组数据，先输出为第几组数据，然后输出最长的海岸线长度。

Sample Input

3
2 2
EE
EE
3 3
EEE
.E.
EEE
3 3
EEE
DED
EEE

Sample Output

Case 1: 8
Case 2: 16
Case 3: 20

Hint

对于第三组样例，一种可行方案是：

.E.
D.D
.E.

这样5个孤立小岛的海岸线总长为4 * 5 = 20。

 

 

 

 

【分析】

　　网络流构图。

　　最小割定理：最小割等于最大流。

　　

　　引用一段：http://www.kuangbin.net/archives/hdu4859

因为E有两个选择D或者.   其实就暗含了最小割的模型。 最小割的话，就是一部分分到源点一侧，一部分分到汇点一侧。

如果把源点分在一起当成是.   和汇点分在一起当成是D.  那么建图的时候，相邻的建流量为1的边。 如果这个点本来是. 那个连汇点是INF，本来是D的，连源点是INF。

如果是这种建图的话，最小割求出来的最小周长。

我们需要的最大周长。

稍微转化下。 我们希望相邻格子不同的最多，其实就是要相邻格子相同的最少。

所以用最小割来求相邻格子相同的最小值，然后总相邻数减掉这个就是答案了。

建图方法就是一开始进行奇偶染色。相当于对于点(x,y)

如果(x+y)%2 == 0 那么当成这个格子是 . 的，和源点分在一起。

如果(x+y)%2 == 1 那么当成这个格子是 D 的，和汇点分在一起。

相邻两点都建边。

这样建图的话，如果在源点一侧的跑到了汇点一侧，那么就相当于这个点从.变到D, 自然相同的数量要减少了、

汇点一侧的跑到了源点一侧，那么就相当于这个点从D变成了.

建图的时候，如果(x+y)%2==0 && 这个点本来就是D  或者 (x+y)%2 == 1 && 这个点本来就是.     那么这个点必须和汇点在一起，就把这个点和源点连INF的边。 相反情况类似处理。

这样建图出来的最小割，一定就是相邻格子是同一类的最小数量。总相邻减掉这个值就是答案了。

 

 

　　即如图所示：

 

　　对于右边绿色的图的情况的（1，1）点和（1，2）点连边如图所示。（蓝色为边的编号，橙色为流量）

　　上面棕色点为（1，1） 下面棕色点为（1，2）

　   割边1表示点（1，1）为陆，割边2表示点（1，1）为海
　   割边4表示点（1，2）为海，割边5表示点（1，2）为陆

　　因为有双向边3，所以当两点同为陆或者海，必须把3号边也割了（花费1），图才能分割开。

　　一开始假设所有有可能的（即不确定的）都是海岸线，建图跑最小割即可。

　　注意相邻两点表示陆海的时候要反过来。

 

　　网络流之前打的模版有点慢，导致我一直TLE，这样做会快一点：

 

AC代码如下：

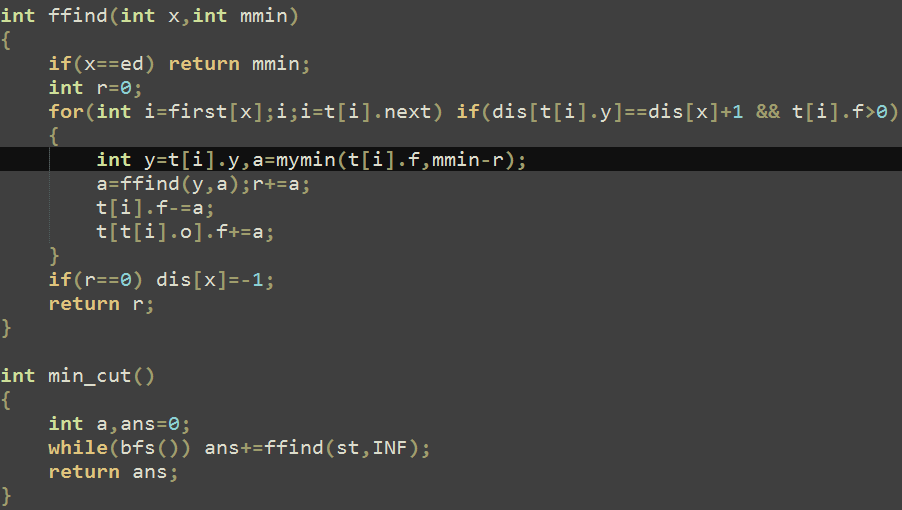
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 using namespace std;
 #define Maxn 4010
 #define Maxm 4010*4
 #define INF 0xfffffff

 char s[];

 int map[][];
 int dx[]={,-,,,},
     dy[]={,,-,,};
 int num[][];
 int s1[][],s2[][];

 struct node
 {
     int x,y,f,o,next;
 }t[Maxm*];int len;

 int st,ed;
 int dis[Maxn],first[Maxn];

 int mymin(int x,int y) {return x<y?x:y;}

 void ins(int x,int y,int f)
 {
     if(f==) return;
     t[++len].x=x;t[len].y=y;t[len].f=f;
     t[len].next=first[x];first[x]=len;t[len].o=len+;
     t[++len].x=y;t[len].y=x;t[len].f=;
     t[len].next=first[y];first[y]=len;t[len].o=len-;
 }

 queue<int > q;
 bool bfs()
 {
     while(!q.empty()) q.pop();
     memset(dis,-,sizeof(dis));
     dis[st]=;q.push(st);
     while(!q.empty())
     {
         int x=q.front();q.pop();
         for(int i=first[x];i;i=t[i].next) if(t[i].f>)
         {
             int y=t[i].y;
             if(dis[y]==-)
             {
                 dis[y]=dis[x]+;
                 q.push(y);
             }
         }
     }
     if(dis[ed]!=-) return ;
     return ;
 }

 int ffind(int x,int mmin)
 {
     if(x==ed) return mmin;
     int r=;
     for(int i=first[x];i;i=t[i].next) if(dis[t[i].y]==dis[x]+ && t[i].f>)
     {
         int y=t[i].y,a=mymin(t[i].f,mmin-r);
         a=ffind(y,a);r+=a;
         t[i].f-=a;
         t[t[i].o].f+=a;
     }
     if(r==) dis[x]=-;
     return r;
 }

 int min_cut()
 {
     int a,ans=;
     while(bfs()) ans+=ffind(st,INF);
     return ans;
 }

 int main()
 {
     int T,kase=,ans;
     scanf("%d",&T);
     while(T--)
     {
         int n,m;
         scanf("%d%d",&n,&m);
         for(int i=;i<=n;i++)
         {
             scanf("%s",s);
             for(int j=;j<m;j++)
             {
                 if(s[j]=='E') map[i][j+]=;
                 else if(s[j]=='.') map[i][j+]=;
                 else map[i][j+]=;
             }
         }

         int ans=*n*m+n+m;
         for(int i=;i<=m+;i++) map[][i]=,map[n+][i]=;
         for(int i=;i<=n+;i++) map[i][]=,map[i][m+]=;

         memset(s1,,sizeof(s1));
         memset(s2,,sizeof(s2));
         for(int i=;i<=n;i++)
          for(int j=;j<=m;j++) if(map[i][j]!=)
          {
              int now=i*(m+)+j;
              for(int k=;k<=;k++)
              {
                  int nx=i+dx[k],ny=j+dy[k];
                  if(map[i][j]==) s1[nx][ny]++;
                  if(map[i][j]==) s2[nx][ny]++;
                  if((nx==||ny==||nx==n+||ny==m+)&&map[i][j]==) ans--;
                  else if(map[nx][ny]!=&&map[nx][ny]==map[i][j]&&k<=)    ans--;
              }
          }
         for(int i=;i<=m;i++) s2[][i]++,s2[n][i]++;
         for(int i=;i<=n;i++) s2[i][]++,s2[i][m]++;
         memset(first,,sizeof(first));
         len=;int cnt=;
         st=,ed=;
         for(int i=;i<=n;i++)
          for(int j=;j<=m;j++) if(map[i][j]==)
          {
              int now=++cnt;num[i][j]=cnt;
              if((i+j)%==) {ins(now,ed,s2[i][j]);ins(st,now,s1[i][j]);}
              else {ins(now,ed,s1[i][j]);ins(st,now,s2[i][j]);}
              for(int k=;k<=;k++)
              {
                  int nx=i+dx[k],ny=j+dy[k];
                  if(nx<||nx>n||ny<||ny>m) continue;
                  if(map[nx][ny]!=) continue;
                  int d=num[nx][ny];
                  ins(now,d,);ins(d,now,);
              }
          }
         ans-=min_cut();
         printf("Case %d: %d\n",++kase,ans);
     }
     return ;
 }

[HDU4859]

2016-05-17 16:42:42