拉普拉斯特征图降维及其python实现
这种方法假设样本点在光滑的流形上,这一方法的计算数据的低维表达,局部近邻信息被最优的保存。以这种方式,可以得到一个能反映流形的几何结构的解。
步骤一:构建一个图G=(V,E),其中V={vi,i=1,2,3…n}是顶点的集合,E={eij}是连接顶点的vi和vj边,图的每一个节点vi与样本集X中的一个点xi相关。如果xi,xj相距较近,我们就连接vi,vj。也就是说在各自节点插入一个边eij,如果Xj在xi的k领域中,k是定义参数。
步骤二:每个边都与一个权值Wij相对应,没有连接点之间的权值为0,连接点之间的权值:
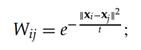
步骤三:令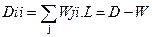 ,实现广义本征分解:
,实现广义本征分解:
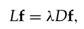
使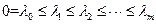 是最小的m+1个本征值。忽略与
是最小的m+1个本征值。忽略与 =0相关的本征向量,选取另外m个本征向量即为降维后的向量。
=0相关的本征向量,选取另外m个本征向量即为降维后的向量。
2.1、python实现拉普拉斯降维
def laplaEigen(dataMat,k,t):
m,n=shape(dataMat)
W=mat(zeros([m,m]))
D=mat(zeros([m,m]))
for i in range(m):
k_index=knn(dataMat[i,:],dataMat,k)
for j in range(k):
sqDiffVector = dataMat[i,:]-dataMat[k_index[j],:]
sqDiffVector=array(sqDiffVector)**2
sqDistances = sqDiffVector.sum()
W[i,k_index[j]]=math.exp(-sqDistances/t)
D[i,i]+=W[i,k_index[j]]
L=D-W
Dinv=np.linalg.inv(D)
X=np.dot(D.I,L)
lamda,f=np.linalg.eig(X)
return lamda,f
def knn(inX, dataSet, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize,1)) - dataSet
sqDiffMat = array(diffMat)**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
return sortedDistIndicies[0:k]
dataMat, color = make_swiss_roll(n_samples=2000)
lamda,f=laplaEigen(dataMat,11,5.0)
fm,fn =shape(f)
print 'fm,fn:',fm,fn
lamdaIndicies = argsort(lamda)
first=0
second=0
print lamdaIndicies[0], lamdaIndicies[1]
for i in range(fm):
if lamda[lamdaIndicies[i]].real>1e-5:
print lamda[lamdaIndicies[i]]
first=lamdaIndicies[i]
second=lamdaIndicies[i+1]
break
print first, second
redEigVects = f[:,lamdaIndicies]
fig=plt.figure('origin')
ax1 = fig.add_subplot(111, projection='3d')
ax1.scatter(dataMat[:, 0], dataMat[:, 1], dataMat[:, 2], c=color,cmap=plt.cm.Spectral)
fig=plt.figure('lowdata')
ax2 = fig.add_subplot(111)
ax2.scatter(f[:,first], f[:,second], c=color, cmap=plt.cm.Spectral)
plt.show()
2.2、拉普拉斯降维实验
用如下参数生成实验数据存在swissdata.dat里面:
def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):
#Generate a swiss roll dataset.
t = 1.5 * np.pi * (1 + 2 * random.rand(1, n_samples))
x = t * np.cos(t)
y = 83 * random.rand(1, n_samples)
z = t * np.sin(t)
X = np.concatenate((x, y, z))
X += noise * random.randn(3, n_samples)
X = X.T
t = np.squeeze(t)
return X, t
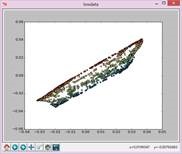
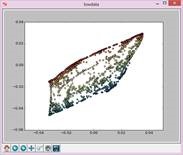
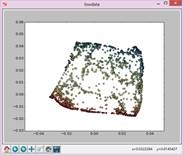
实验结果如下:
N=5,t=15: N=7,t=15: N=9,t=15:
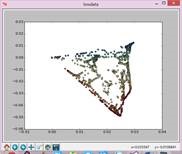
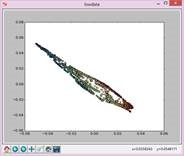
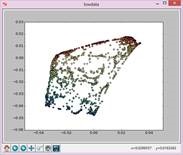
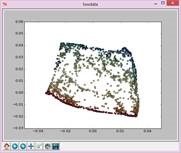
N=11,t=15: N=13,t=15: N=15,t=15:
N=17,t=15: N=19,t=15: N=21,t=15:
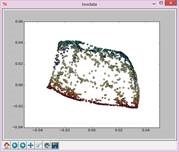
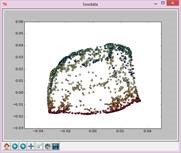
N=23,t=15: N=25,t=15: N=27,t=15:
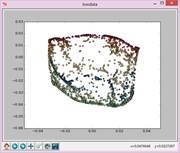
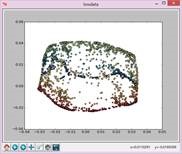
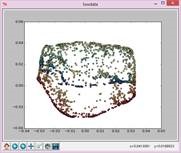
N=29,t=15: N=31,t=15: N=33,t=15:
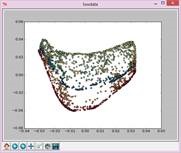
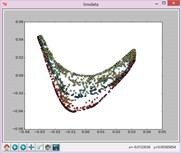
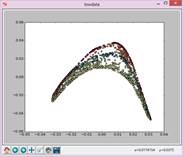
N=25,t=5: N=25,t=8: N=25,t=10:
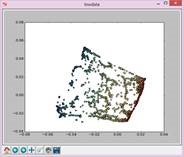
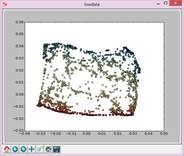

N=25,t=12: N=25,t=14: N=25,t=50:
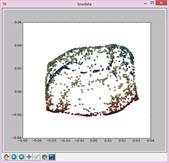
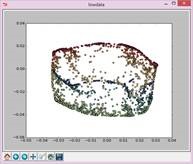
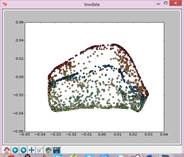
N=25,t=Inf:
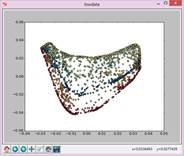
拉普拉斯特征图降维及其python实现的更多相关文章
- LBP特征学习(附python实现)
LBP的全称是Local Binary Pattern即局部二值模式,是局部信息提取中的一种方法,它具有旋转不变性和灰度不变性等显著的优点.在人脸识别领域有很多案例,此外,局部特征的算法还有 SIFT ...
- 拉普拉斯特征映射(Laplacian Eigenmaps)
1 介绍 拉普拉斯特征映射(Laplacian Eigenmaps)是一种不太常见的降维算法,它看问题的角度和常见的降维算法不太相同,是从局部的角度去构建数据之间的关系.也许这样讲有些抽象,具体来讲, ...
- GhostNet: 使用简单的线性变换生成特征图,超越MobileNetV3的轻量级网络 | CVPR 2020
为了减少神经网络的计算消耗,论文提出Ghost模块来构建高效的网络结果.该模块将原始的卷积层分成两部分,先使用更少的卷积核来生成少量内在特征图,然后通过简单的线性变化操作来进一步高效地生成ghost特 ...
- 以图搜图(一):Python实现dHash算法(转)
近期研究了一下以图搜图这个炫酷的东西.百度和谷歌都有提供以图搜图的功能,有兴趣可以找一下.当然,不是很深入.深入的话,得运用到深度学习这货.Python深度学习当然不在话下. 这个功能最核心的东西就是 ...
- 卷积神经网络特征图可视化(自定义网络和VGG网络)
借助Keras和Opencv实现的神经网络中间层特征图的可视化功能,方便我们研究CNN这个黑盒子里到发生了什么. 自定义网络特征可视化 代码: # coding: utf-8 from keras.m ...
- Keras中间层输出的两种方式,即特征图可视化
训练好的模型,想要输入中间层的特征图,有两种方式: 1. 通过model.get_layer的方式.创建新的模型,输出为你要的层的名字. 创建模型,debug状态可以看到模型中,base_model/ ...
- 卷积网络中的通道(Channel)和特征图
转载自:https://www.jianshu.com/p/bf8749e15566 今天介绍卷积网络中一个很重要的概念,通道(Channel),也有叫特征图(feature map)的. 首先,之前 ...
- SLAM概念学习之特征图Feature Maps
特征图(或者叫地标图,landmark maps)利用参数化特征(如点和线)的全局位置来表示环境.如图1所示,机器人的外部环境被一些列参数化的特征,即二维坐标点表示.这些静态的地标点被观测器(装有传感 ...
- 深度学习之加载VGG19模型获取特征图
1.加载VGG19获取图片特征图 # coding = utf-8 import tensorflow as tf import numpy as np import matplotlib.pyplo ...
随机推荐
- dataTable 禁止排序
$("#id").DataTable({ "ordering": false, // 禁止排序 });
- LAMP虚拟主机配置以及控制目录访问
3.基于域名的虚拟主机配置 NameVirtualHost192.168.3.32:80#apache2.2.xx版本需要开启此选项,而且要和下面的保持一致:2.4.x版本就不需要此项设置了 < ...
- 转载:STM32之中断与事件---中断与事件的区别
这张图是一条外部中断线或外部事件线的示意图,图中信号线上划有一条斜线,旁边标志19字样的注释,表示这样的线路共有19套.图中的蓝色虚线箭头,标出了外部中断信号的传输路径,首先外部信号从编号1的芯片管脚 ...
- Nhibernate配置和访问数据问题
今天开始用Nhibernate做为自己的ORM,但是做的过程中确实遇到了好多问题,现在将问题收集起来以防日后出现相同的问题, 总结下: 这就是我的整个项目,现在配置下hibernate.cfg.xml ...
- python multiprocessing 多进程
''' 如果要启动大量的子进程,可以用进程池的方式批量创建子进程: ''' def test_task(name): print 'Run task %s (%s)...' % (name, os.g ...
- new 的用法
在C#中,new关键字有三种用法: 1.new 运算符,用于创建对象和调用构造函数. 2.new 修饰符,在用作修饰符时,new关键字可以显式隐藏从基类继承的成员. 3.new 约束 ,用于在泛型 ...
- HttpOnly
Contents 1 Overview 1.1 Who developed HttpOnly? When? 1.2 What is HttpOnly? 1.3 Mitigating the Most ...
- win7系统64位eclipse环境超详细暗黑1.4服务器搭建
原地址:http://bbs.gameres.com/thread_223704.html 今天闲来没事,参照论坛中几篇成功案例,自己也搭建了下服务端,这里详细的记录下我的安装过程,方便大家快速搭建. ...
- POJ 3007 Organize Your Train part II(哈希链地址法)
http://poj.org/problem?id=3007 题意 :给你一个字符串,让你无论从什么地方分割,把这个字符串分成两部分s1和s2,然后再求出s3和s4,让你进行组合,看能出来多少种不同的 ...
- Android USB Host 与 Hid 设备通信bulkTransfer()返回-1问题的原因
近期一直在做Android USB Host 与USB Hid设备(STM32FXXX)的通信,遇到了很多问题.项目源码以及所遇到的其他问题可以见本博客其他相关文章,这里重点讲一下bulkTransf ...
