【HDU2815】【拓展BSGS】Mod Tree

Problem Description

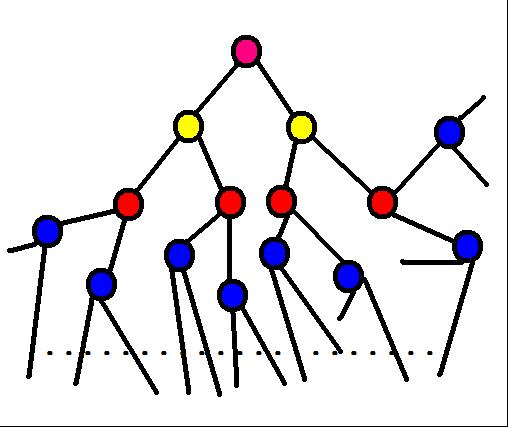
  The picture indicates a tree, every node has 2 children.
  The depth of the nodes whose color is blue is 3; the depth of the node whose color is pink is 0.
  Now
out problem is so easy, give you a tree that every nodes have K
children, you are expected to calculate the minimize depth D so that the
number of nodes whose depth is D equals to N after mod P.

 

Input

The input consists of several test cases.
Every cases have only three integers indicating K, P, N. (1<=K, P, N<=10^9)

 

Output

The minimize D.
If you can’t find such D, just output “Orz,I can’t find D!”

 

Sample Input

3 78992 453
4 1314520 65536
5 1234 67

 

Sample Output

Orz,I can’t find D!
8
20

Author

AekdyCoin

 

Source

HDU 1st “Old-Vegetable-Birds Cup” Programming Open Contest

Recommend

lcy   |   We have carefully selected several similar problems for you:  2814 2809 3037 2447 2810

【分析】

普通的BSGS是只能够解决A^x = B(mod C),其中C为素数的形式，而通过网上的消元的方法能够解决这种问题。

同样BSGS直接解决C为素数的形式也是可以的.

 /*
 宋代晏几道
 《生查子·狂花顷刻香》
 狂花顷刻香，晚蝶缠绵意。天与短因缘，聚散常容易。
 传唱入离声，恼乱双蛾翠。游子不堪闻，正是衷肠事。
 */
 #include <iostream>
 #include <cstdio>
 #include <ctime>
 #include <cmath>
 #include <algorithm>
 #include <cstring>
 #include <string>
 #include <map>
 #include <set>
 #include <vector>
 #define LOCAL
 const int MAXN =  + ;
 const int INF = 0x7fffffff;
 using namespace std;
 typedef long long LL;

 int gcd(int a, int b ){return b ==  ? a : gcd(b, a % b);}
 int ext_gcd(int a, int b, int &x, int &y){
     if (b == ) {x = ; y = ; return a;}
     int tmp = ext_gcd(b, a % b, y, x);
     y -= x * (a / b);
     return tmp;
 }
 //求解
 int Inval(int a, int  b, int n){
     int x, y, e;
     ext_gcd(a, n, x, y);
     e = (LL) x * b % n;//小心超出int 的范围,因为a,n是互质的，因此求解出来的结果就是ax + ny = 1，乘以b才正确的答案
     return e <  ? e + n : e;
 }
 // k s m
 int pow_mod(LL a, int b, int c){
     if (b == ) return a % c;
     LL tmp = pow_mod(a, b / , c);
     if (b %  == ) return (tmp * tmp) % c;
     else return (((tmp * tmp) % c) * a) % c;
 }
 int BSGS(int A, int B, int C){
     map<int, int> H;//hash
     LL buf =  % C, D = buf, K;
     int d = , tmp;
     //小步
     for (int i = ; i <= ; buf = buf * A % C, i++)
     if (buf == B) return i;
     //消因子
     while ((tmp = gcd(A, C)) != ){
           if (B % gcd(A, C) != ) return -;//为了解不定方程
           d++;
           C /= tmp;
           B /= tmp;
           D = D * A / tmp % C;
     }
     H.clear();
     int M = (int)ceil(sqrt(C * 1.0));
     buf =  % C;
     for (int i = ; i <= M; buf = buf * A % C, i++)
     if (H.find((int)buf) == H.end()) H[(int)buf] = i;//Hash

     K = pow_mod ((LL) A, M, C);
     for (int i = ; i <= M; D = D * K % C, i++){
         tmp = Inval((int) D ,B, C);//D和C是互质的
         //一定不要忘了最后的d
         if (tmp >=  && H.find(tmp) != H.end()) return i * M + H[tmp] + d;
     }
     return -;//找不到
 }
 int main(){

     //转换为A^x = B(mod C)的形式
     int A, B, C;
     while (scanf("%d%d%d", &A, &C, &B) != EOF){
           if (B >= C) {printf("Orz,I can’t find D!\n"); continue;}//
           int tmp = BSGS(A, B, C);
           if (tmp < ) printf("Orz,I can’t find D!\n");
           else printf("%d\n", tmp);
     }
     return ;
 }