各种分布（distribution）

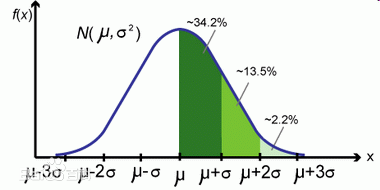
正态分布(Normal distribution)，又名高斯分布(Gaussian distribution)。若随机变量X服从一个数学期望为μ、方差为σ^2(标准差为σ)的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

当μ = 0,σ = 1时的正态分布是标准正态分布。正态分布转换为标准正态分布的公式：

概率密度函数，纵坐标f(x)是一个值，即概率密度，面积积分起来就是概率。

均匀分布

(1) 如果

,则称X服从离散的均匀分布。

(2) 设连续型随机变量X的概率密度函数为

则称随机变量X服从[a,b]上的均匀分布，记为X~U(a,b)。

均匀分布概率密度函数：

 

 

伯努利分布、二项分布、多项分布、Beta分布、Dirichlet分布

http://blog.csdn.net/michael_r_chang/article/details/39188321