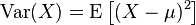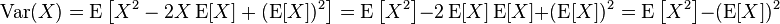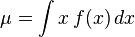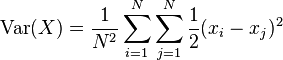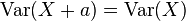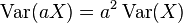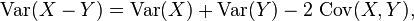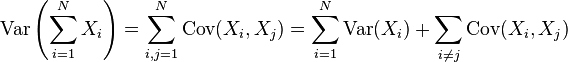方差var,标准差
wiki摘录如下(红色字体是特别标注的部分):
方差:http://zh.wikipedia.org/wiki/%E6%96%B9%E5%B7%AE
方差
变异量(数)(Variance),应用数学里的专有名词。在概率论和统计学中,一个随机变量的方差描述的是它的离散程度,也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差,恰巧也是它的二阶累积量。方差的算术平方根称为该随机变量的标准差。
标准差才是变量离其期望值的距离,方差应该是距离的平方
以下的所有定义,都有平均值EX,其实在实际中很多时候会先将变量去中心化,也就是让变量的均值为0。带着这个想法看下面的定义,公式会变得更加简洁一些。
目录
[隐藏]
定义
设X为服从分布F的随机变量, 如果E[X]是随机变量X的期望值(平均数μ=E[X])
随机变量X或者分布F的方差为:
这个定义涵盖了连续、离散、或两者都有的随机变量。方差亦可当作是随机变量与自己本身的协方差:
方差典型的标记有Var(X),  , 或是
, 或是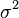 ,其表示式可展开成为:
,其表示式可展开成为:
上述的表示式可记为"平方的平均减掉平均的平方"
连续随机变量
如果随机变量X是连续分布,并对应至概率密度函数f(x),则其方差为:
此处 是一期望值,
是一期望值,
且此处的积分为以X为范围的x定积分(definite integral)
如果一个连续分布不存在期望值,如柯西分布(Cauchy distribution),也就不会有方差。
离散随机变量
如果随机变量X是具有概率质量函数的离散概率分布x1 ↦ p1, ..., xn ↦ pn,则:
此处 是其期望值, i.e.
是其期望值, i.e.
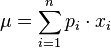 .
.
当X为有N个相等概率值的平均分布:
N个相等概率值的方差亦可以点对点间的方变量表示为:
特性
方差不会是负的,因为次方计算为正的或为零:
一个常数随机变量的方差为零,且当一个资料集的方差为零时,其内所有项目皆为相同数值:
方差不变于定位参数的变动。也就是说,如果一个常数被加至一个数列中的所有变量值,此数列的方差不会改变:
如果所有数值被放大一个常数倍,方差会放大此常数的次方倍:
两个随机变量合的方差为:
此数Cov(., .)代表协方差。
对于 个随机变量
个随机变量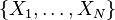 的总和:
的总和:
在样本空间Ω上存在有限期望和方差的随机变量构成一个希尔伯特空间: L2(Ω, dP),不过这里的内积和长度跟方差,标准差还是不大一样。 所以,我们得把这个空间“除”常变量构成的子空间,也就是说把相差一个常数的 所有原来那个空间的随机变量做成一个等价类。这还是一个新的无穷维线性空间, 并且有一个从旧空间内积诱导出来的新内积,而这个内积就是方差
一般化
如果X是一个向量其取值范围在实数空间Rn,并且其每个元素都是一个一维随机变量,我们就把X称为随机向量。随机向量的方差是一维随机变量方差的自然推广,其定义为E[(X − μ)(X − μ)T],其中μ = E(X),XT是X的转置。这个方差是一个非负定的方阵,通常称为协方差矩阵。
如果X是一个复数随机变量的向量(向量中每个元素均为复数的随机变量),那么其方差定义则为E[(X − μ)(X − μ)*],其中X*是X的共轭转置向量或称为埃尔米特向量。根据这个定义,变异数为实数。
方差var,标准差的更多相关文章
- 使用java计算数组方差和标准差
使用java计算数组方差和标准差 觉得有用的话,欢迎一起讨论相互学习~Follow Me 首先给出方差和标准差的计算公式 代码 public class Cal_sta { double Sum(do ...
- Python求均值,方差,标准差
import numpy as nparr = [1,2,3,4,5,6]#求均值arr_mean = np.mean(arr)#求方差arr_var = np.var(arr)#求标准差arr_st ...
- python求列表均值,方差,标准差
import numpy as np a = [1,2,3,4,5,6] #求均值 a_mean = np.mean(a) #求方差 a_var = np.var(a) #求标准差 a_std = n ...
- 使用oracle来计算方差及标准差
/* Formatted on 5/24/2012 4:15:58 PM (QP5 v5.149.1003.31008) */ SELECT deptno, ename, ...
- 【Udacity】数据的差异性:值域、IQR、方差和标准差
一.值域(Range) Range = Max - Min 受异常值(Outliers)影响 二.四分位差(IQR) 四分位距(interquartile range, IQR),又称四分差.是描述统 ...
- arcpy-字段唯一值、重复值、最值、平均值、方差、标准差、中数、众数
插个广告,制作ArcGIS的Tool工具学习下面的教程就对了: 零基础学习Python制作ArcGIS自定义工具观看链接 <零基础学习Python制作ArcGIS自定义工具>课程简介 im ...
- 方差(variance)、标准差(Standard Deviation)、均方差、均方根值(RMS)、均方误差(MSE)、均方根误差(RMSE)
方差(variance).标准差(Standard Deviation).均方差.均方根值(RMS).均方误差(MSE).均方根误差(RMSE) 2017年10月08日 11:18:54 cqfdcw ...
- 平均值(Mean)、方差(Variance)、标准差(Standard Deviation) (转)
http://blog.csdn.net/xidiancoder/article/details/71341345 平均值 平均值的概念很简单:所有数据之和除以数据点的个数,以此表示数据集的平均大小: ...
- C语言之文件操作07——读取文件数据并计算均值方差标准差
//文件 /* =============================================================== 题目:从文本文件"high.txt" ...
随机推荐
- python list列表 方法总结
深入链表(most on lists) The list data type has some more methods. Here are all of the methods of list ob ...
- 非常棒的Java REST服务器栈
Dropwizard 是一个开源的Java框架,用于开发OPS友好.高性能的基于REST的后端.它是由Yammer开发的,来驱动基于JVM的后端. Dropwizard提供同类最佳的Java库到一个嵌 ...
- C语言随笔_printf输出多行
想在printf中,输出多行数据,如果写成下面这样: printf("line 1\n line 2\n line 3\n");编译器会报错“error C2001: newlin ...
- 产生n bit所有可能的序列
void binary(int n) { ) printf("%s\n",A); // Assume A is a global variable else { A[n-] = ' ...
- hdu 2079 选课时间_母函数
题意:需要学够n学分,有k个情况(x学分,y个相同学分的课) 解法:套母函数模板 #include <iostream> #include<cstdio> using name ...
- MyCat 主键ID自增长配置
在实现分库分表的情况下,数据库自增主键已无法保证自增主键的全局唯一.为此,MyCat 提供了全局sequence,并且提供了包含本地配置和数据库配置等多种实现方式,实现方式主要有三种:本地文件方式.数 ...
- 了解XSS攻击
XSS又称CSS,全称Cross SiteScript,跨站脚本攻击,是Web程序中常见的漏洞,XSS属于被动式且用于客户端的攻击方式,所以容易被忽略其危害性.其原理是攻击者向有 XSS漏洞的网站中输 ...
- org.springframework.web.util.IntrospectorCleanupListener的用途
Spring官方API中对其描述如下 /** * Listener that flushes the JDK's {@link java.beans.Introspector JavaBeans In ...
- java基础之集合List-ArrayList、LinkedList、Vector的差别
PS:本篇博客主要參考jdk的底层源代码.而非自己动手写代码. 请问ArrayList.LinkedList.Vector的差别 ①ArrayList底层实际上是採用数组实现的(而且该数组的类型的Ob ...
- Ubuntu14.04搭建安装svnserver
前两天,公司准备搭建一个svnserver,供大家使用.于是.就先装了一个Ubuntu系统,然后搭建了svnserver的环境.以下把svn搭建的详细过程描写叙述下: 1.安装svn sudo apt ...