栈常考应用之括号匹（C++）

思路在注释里。还是使用链栈的API，为啥使用链栈呢，因为喜欢链栈。

//header.h
#pragma once
#include<iostream>
using namespace std;
template<class T>
struct LinkNode						//节点类定义
{
	T data;						//数据域
	LinkNode<T> *next;				//链指针域
	LinkNode(LinkNode<T> *ptr = NULL){this->next = ptr;}	//初始化指针域的构造函数
	LinkNode(const T& item, LinkNode<T> *ptr = NULL)//初始化数据成员和指针成员和指针的构造函数
	{
		this->data = item;
		this->next = ptr;
	}
};

template<class T>
class ListStack		//用头结点的数据域表示链表元素数量
{
protected:
	LinkNode<T> *first;
public:
	ListStack(){first = new LinkNode<T>;first->data = 0;}//无参数构造
	ListStack(const T& x)
	{
		this->first = new LinkNode<T>;
		this->input(x);
	}//含有参数的构造函数
	ListStack(ListStack<T>& L);//拷贝构造
	~ListStack(){makeEmpty();}//析构函数
	void makeEmpty();//将链表置空的函数
	int Length()const{return this->first->data;}//计算链表长度的函数
	LinkNode<T>* getHead()const{return this->first;}//返回附加头结点地址
	LinkNode<T>* getRear()const;//返回尾部指针
	void input(T head);//头插
	void output();//将链表打印出来
	bool Remove(int i, T& x);
	bool IsEmpty()const{return !this->first->data;}
	bool outstack(T& x);

};
template<class T>
bool ListStack<T>::outstack(T& x)
{
	return this->Remove(1, x);
}
template<class T>
bool ListStack<T>::Remove(int i, T& x)
{
	if(i>0 && i<=this->first->data)
	{
		LinkNode<T> *tmp = this->first, *p;
		if(i!=1)
		{
			int j = 0;
			while(j!=i-1)
			{
				tmp = tmp->next;
				++j;
			}
			p = tmp->next;
			tmp->next = p->next;
			x = p->data;
			delete p;
		}
		else
		{
			p = tmp->next;
			x = p->data;
			tmp->next = p->next;
			delete p;
		}
		--this->first->data;
		return true;
	}
	return false;
}

template<class T>
void ListStack<T>::input(T head)
{
	LinkNode<T> *tmp = new LinkNode<T>;
	if(tmp == NULL)
	{
		cerr<<"内存分配错误！\n"<<endl;
		exit(-1);
	}

	if(this->first->next != NULL)
	{
		tmp->next = this->first->next;
		this->first->next = tmp;
	}
	else
	{
		this->first->next = tmp;
		tmp->next = NULL;
	}
	tmp->data = head;
	++this->first->data;

}
template<class T>
void ListStack<T>::output()
{
	LinkNode<T> *p = this->first->next;
	while(p!=NULL)
	{
		cout<<p->data<<" | ";
		p = p->next;
	}
	cout<<"over"<<endl;
}
template<class T>
ListStack<T>::ListStack(ListStack<T>& L)
{
	T value;
	LinkNode<T> *srcptr = L.getHead();
	LinkNode<T> *desptr = this->first = new LinkNode<T>;
	this->first->data = srcptr->data;
	while(srcptr->next != NULL)
	{
		value = srcptr->next->data;
		desptr->next = new LinkNode<T>(value);
		desptr = desptr->next;
		srcptr = srcptr->next;
	}
	desptr->next = NULL;
}
template<class T>
void ListStack<T>::makeEmpty()
{
	LinkNode<T> *p, *q = this->first->next;
	this->first->data = 0;
	while(q != NULL)
	{
		p = q;
		q = q->next;
		delete p;
	}
}
template<class T>
LinkNode<T>* ListStack<T>::getRear()const
{
	LinkNode<T> *p = this->first;
	while(p->next!=NULL)
		p = p->next;
	return p;

}
/*
template<class T>
int List<T>::Length()const
{
	LinkNode<T> *p = this->first->next;
	int count = 0;
	while(p != NULL)
	{
		++count;
		p = p->next;
	}

};*/
//template<class T>

仅是将链栈的del函数修改为outstack

思路如下

#include"header.h"
//设计思路，首先是一个大循环①，匹配到左括号都让其进栈②，一旦入栈发现是右括号，出栈一个括号，检查左右是否匹配，不匹配则匹配失败③，若匹配成功继续入栈④，若无元素可入栈，检测栈空否⑤，空则匹配成功，否则匹配失败
bool match(const char *p)
{
	ListStack<char> st;
	char outchar;
	int i = 0;
	while(p[i]!='\n')//①
	{
		switch(p[i])
		{
			case '('://②
				st.input(p[i]);
				++i;
				break;
			case '['://②
				st.input(p[i]);
				++i;
				break;
			case '{'://②
				st.input(p[i]);
				++i;
				break;
			case '<'://②
				st.input(p[i]);
				++i;
				break;
			case ')'://③④
				st.outstack(outchar);
				if(outchar == '(')
				{
					++i;
					continue;
				}
				return false;
			case ']'://③④
				st.outstack(outchar);
				if(outchar == '[')
				{
					++i;
					continue;
				}
				return false;
			case '}'://③④
				st.outstack(outchar);
				if(outchar == '{')
				{
					++i;
					continue;
				}
				return false;
			case '>'://③④
				st.outstack(outchar);
				if(outchar == '<')
				{
					++i;
					continue;
				}
				return false;
			default:
				++i;
				continue;

		}
	}
	if(st.IsEmpty())//⑤
		return true;
	return false;
}
int main()
{
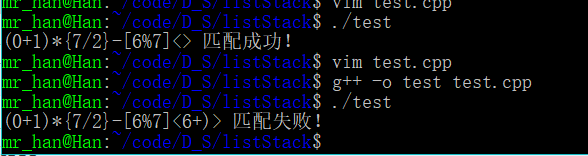
	const char *p = "(0+1)*{7/2}-[6%7]<>";
	if(match(p))
		cout<<p<<" 匹配成功！"<<endl;
	else
		cout<<p<<" 匹配失败！"<<endl;
	return 0;
}

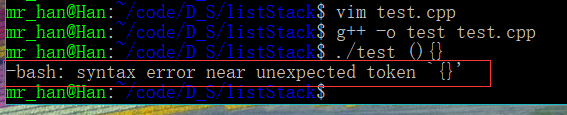
本来打算使用主函数传参将括号字符串传入函数，但是由于主函数参数不能为()和{}

如果我用主函数参数传参则

用了两个字符串来试试