Grids

Grids

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 717    Accepted Submission(s): 296

Problem Description

　　度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

 

Input

　　第一行为数据组数T(1<=T<=100000)。
　　然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

 

Output

　　对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

 

Sample Input

2

1

3

 

Sample Output

Case #1:
1

Case #2:
5

Hint

对于第二组样例，共5种方案，具体方案为：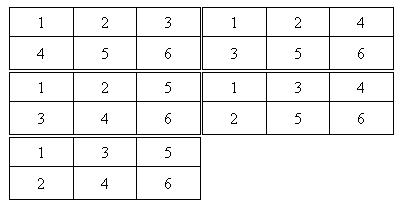

 

Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

 思路：卡特兰数+费马小定理求逆元;

为啥是卡特兰数，我们把第一行看成是入栈，第二行看成是出栈，那么观察下1只能放在第一，接下来我们需要放2，2可以放在2个位置，1.放在1的下边，那么此时3就只能放在第一行的第二个，这就表示1出栈了，那么3需要进栈，2.放在第一行的第二个的话，那么3可以放在1的下端，也可以放在第一行的第3个.....

那么我们从中可以知道只要队列不空那么当前的数就可以放在下边，并且是下边没放的第一个，这样后来的数大，就保证了升序合法，同样放上面也是这个原则，所以这个就和火车入栈出栈一样，是卡特兰数的应用。然后递推下卡特兰数，取模时费马小定理求下逆元即可。

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string.h>
 5 #include<queue>
 6 #include<stack>
 7 #include<set>
 8 #include<math.h>
 9 using namespace std;
10 typedef long long LL;
11 const int N=1e9+7;
12 LL dp[1000005];
13 LL quick(LL n,LL m);
14 int main(void)
15 {
16         int i,j,k;
17         dp[1]=1;
18         dp[2]=2;
19         dp[3]=5;
20         for(i=4; i<=1000000; i++)
21         {
22                 dp[i]=dp[i-1]*(4*i-2)%N;
23                 dp[i]=dp[i]*quick((LL)(i+1),N-2)%N;
24         }
25         scanf("%d",&k);
26         int s;
27         int t;
28         for(s=1; s<=k; s++)
29         {
30                 scanf("%d",&t);
31                 printf("Case #%d:\n",s);
32                 printf("%lld\n",dp[t]);
33         }
34         return 0;
35 }
36 LL quick(LL n,LL m)
37 {
38         LL ak=1;
39         while(m)
40         {
41                 if(m&1)
42                 {
43                         ak=ak*n%N;
44                 }
45                 n=(n*n)%N;
46                 m/=2;
47         }
48         return ak;
49 }