作者自我介绍：大爽歌, b站小UP主 ，

python1对1辅导老师，

时常直播编程，直播时免费回答简单问题。

前置知识： 递归算法(recursion algorithm)。

我的递归教程: 【教程】python递归三部曲（基于turtle实现可视化）

回溯与递归的关系：

回溯是一种算法思想，递归是实现方式。

回溯法经典问题：

八皇后问题、数独问题。

（其实两个很像）

八皇后问题

八皇后问题是一个以国际象棋为背景的问题：

如何在8×8的国际象棋棋盘上放置八个皇后，使其不互相攻击。

即任两个皇后都不能处于同一条横行、纵行或斜线上。

n皇后问题

八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。

(当且仅当n = 1 或 n ≥ 4时问题有解)

4皇后问题!

八皇后讨论起来比较麻烦，先讨论四皇后情况(n=4)

首先展示下错误的情况:

如上图所示，三个图的错误分别是

  1. 第一行有重复了
  2. 对角线有重复了。(注意有两个对角线)
  3. 第一列有重复

想要正确，则每一行每一列，每个对角线(对角线有两个方向)都不能有重复项。

正确的情况示例如下：

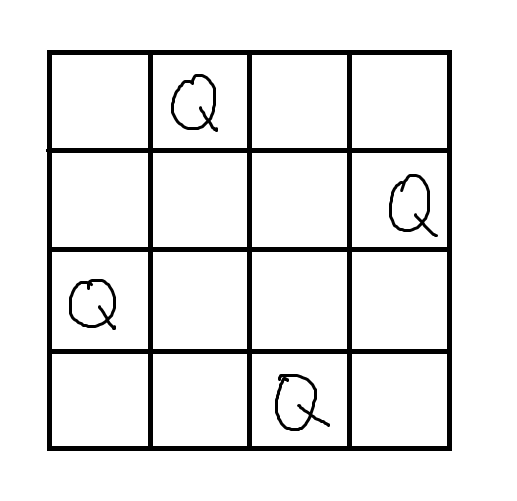
回溯法

回溯法(backtracking)是暴力搜索法中的一种。

其核心思想就是不断尝试，不行就后退再试其他的。

关于这一思想，我之前有个视频，感觉能比较形象地展示，感兴趣可以看看：

迷宫探索动画

接下来我们用回溯法探究下刚才的4皇后问题。

回溯法过程展示

个人感觉用行列坐标表示不够直观，所以给每个格子从前往后依次编号。

后面用编号来称呼位置（无特殊说明的话）

如下图

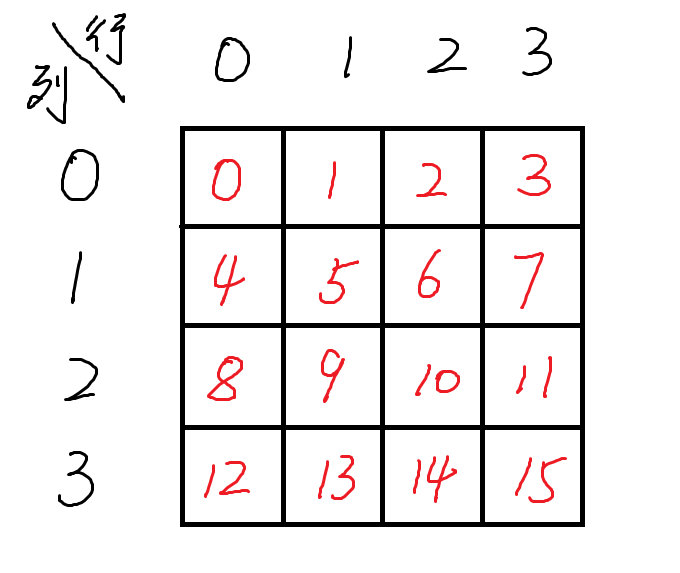
同时四个皇后从前往后按次序编为

\(Q_1\)、\(Q_2\)、\(Q_3\)、\(Q_4\)

原始的回溯法

每次会从前往后依次尝试每个编号的位置。

为了简化谈论，以下先进行了一定的优化。

由于每行不能重复，n个皇后必须分别放在n行上。

当有一行放不下了时。也就失败了。

所以

\(Q_1\)必须放在第一行(行索引为0)

\(Q_2\)必须放在第二行(行索引为1)

\(Q_3\)必须放在第三行(行索引为2)

\(Q_4\)必须放在第四行(行索引为3)

1 \(Q_1\)放位置0

使用回溯法，\(Q_2\)仍然会从0开始尝试，发现放不了，就往后走。

由于\(Q_1\)放位置0。所以

0、1、2、3、

4、8、12、

5、10、15都放不了

\(Q_2\)从第二行开头试。

即从4、5开始试，一直试到6才能够放下，那么就先放在这里。

\(Q_2\)放位置6

那么接下来继续尝试\(Q_3\)，

会发现第三行(行索引为2)已经放不了了。

如下图

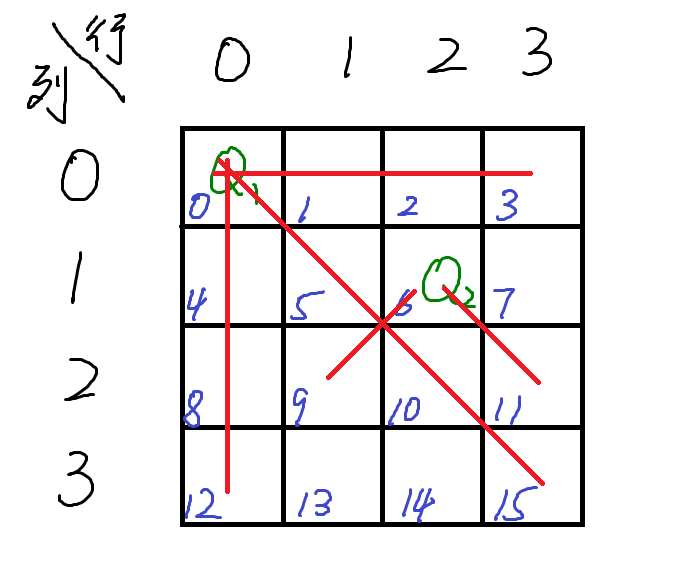
这说明

\(Q_2\)放位置6失败

回来重新放\(Q_2\)，放位置7

\(Q_2\)放位置7

此时\(Q_3\)唯一能放的位置只有9。

之后，\(Q_4\)已经无处可放。

如下图

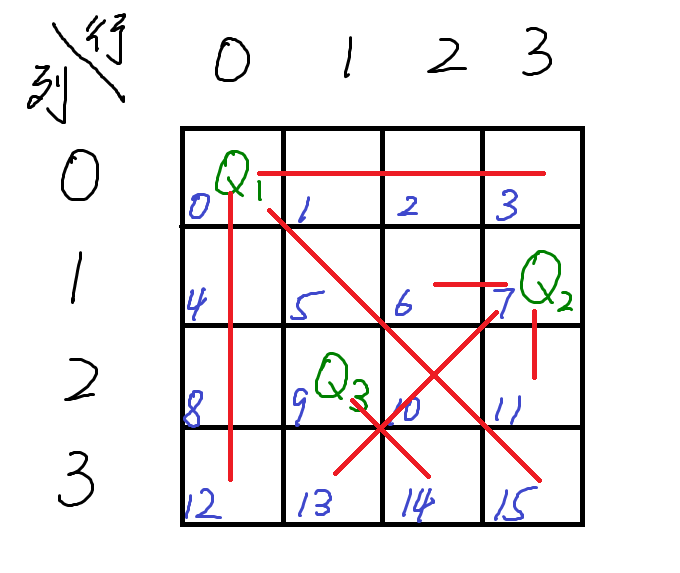
这说明

\(Q_2\)放位置7失败

\(Q_2\)无位置可放

\(Q_2\)无位置可放，

说明\(Q_1\)放在位置0失败。

\(Q_1\)需要尝试其他位置，即尝试先放在位置1。

到这里回溯法的特点其实就已经展现的比较够了：

即不断向下尝试，如果所有尝试都失败，那就后退一步，重新尝试。

2 \(Q_1\)放位置1

此时\(Q_2\)只能放在位置7，

之后\(Q_3\)只能放在位置8，

最后\(Q_3\)只能放在位置14，

即如下图所示

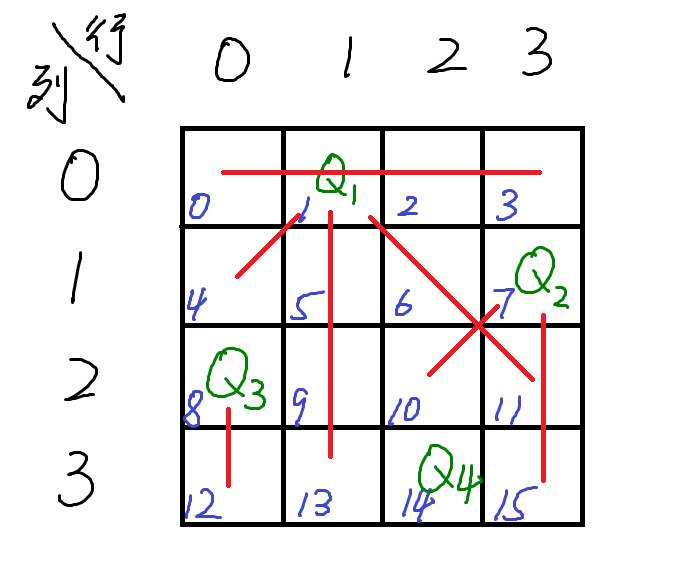
到这里，如果只要求找到一个解法，问题就已经结束了，如果要找到所有解法，那就是继续往后不断尝试。

代码实现

原始回溯法代码

class NQueens:

    def __init__(self, n):

        self.n = n

        # 保存每个皇后的坐标, (ci, ri)

        # 第一行第一列的皇后坐标为(0, 0)

        self.one_solution = []

    def check_can_place(self, ri, ci):

        for pos in self.one_solution:

            pc, pr = pos

            if pc == ci:  # 行检测

                return False

            if pr == ri:  # 列检测

                return False

            if pr - pc == ri - ci:  # 对角线检测 1

                return False

            if pr + pc == ri + ci:  # 对角线检测 2

                return False

        return True

    def solve(self):

        for ri in range(self.n):

            for ci in range(self.n):

                if self.check_can_place(ri, ci):

                    pos = (ci, ri)

                    self.one_solution.append(pos)

                    if len(self.one_solution) == self.n:

                        return True

                    res = self.solve()

                    if res:

                        return True

                    else:

                        self.one_solution.pop()

        return False

    def show_in_board(self):

        board = [

            ["-" for i in range(self.n)] for j in range(self.n)

        ]

        for pos in self.one_solution:

            pc, pr = pos

            board[pr][pc] = "Q"

        for row in board:

            print(" ".join(row))

nq = NQueens(8)

res = nq.solve()

if res:

    print("Queens positions:")

    print(nq.one_solution)

    print("Queens in board:")

    nq.show_in_board()

输出结果

Queens positions:

[(0, 0), (4, 1), (7, 2), (5, 3), (2, 4), (6, 5), (1, 6), (3, 7)]

Queens in board:

Q - - - - - - -

- - - - Q - - -

- - - - - - - Q

- - - - - Q - -

- - Q - - - - -

- - - - - - Q -

- Q - - - - - -

- - - Q - - - -

check_can_place方法

该方法，用于检查指定的横纵坐标，是否还能防止皇后（不与已经放置的皇后冲突）

检查是否能放置

行和列好分析，对角线情况则比较麻烦。

两种对角线图示如下

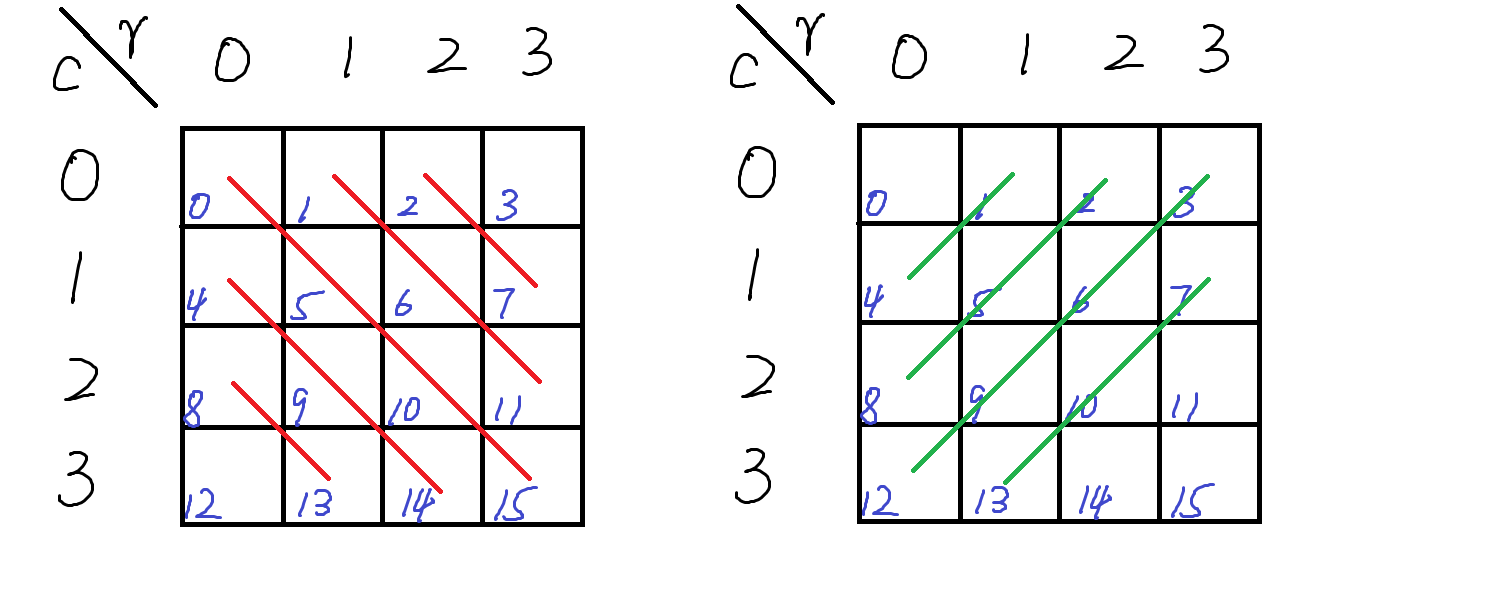
第一种对角线（红色对角线）

每一条对角线上格子，\(r-c\)都是相同的值。

可以通过这个值来判断是否在同一条对角线上。

第二种对角线（绿色对角线）

每一条对角线上格子，\(r+c\)都是相同的值。

可以通过这个值来判断是否在同一条对角线上。

solve方法解析

def solve(self):

    for ri in range(self.n):

        for ci in range(self.n):

            # 从前往后尝试所有的位置，看是否能放皇后

            if self.check_can_place(ri, ci):

                # 成功则添加

                pos = (ci, ri)

                self.one_solution.append(pos)

                if len(self.one_solution) == self.n:

                    # 皇后数量已到达n，问题解决，返回解决成功

                    return True

                # 走到这里，说明还没解决

                # 递归调用自身，看当前情况往后是否能够解决成功

                res = self.solve()

                if res:

                    # 成功，就继续返回解决成功

                    return True

                else:

                    # 失败，之前添加的pos方法，是不成功的，将其弹出，之后继续尝试

                    self.one_solution.pop()

    return False

代码优化与拓展

优化：一行一试

上面的原始回溯法的代码。

每一次放皇后都是从前往后一个一个试，效率很低。

这里按照上文讨论中的思路进行优化，

即每一行放一个皇后。

那么代码里面就是每一行，从第一列开始一直尝试到最后一列。

一行放好后，就往下一行进行尝试。

这里只需要给NQueens类添加一个新方法solve_advanced即可

def solve_advanced(self, ri=0):

    for ci in range(self.n):

        if self.check_can_place(ri, ci):

            pos = (ci, ri)

            self.one_solution.append(pos)

            if ri == self.n - 1:

                return True

            res = self.solve_advanced(ri+1)

            if res:

                return True

            else:

                self.one_solution.pop()

    return False

调用时的res = nq.solve()改成res = nq.solve_advanced()即可。

输出和原始回溯法时的输出是一样的。

不过代码运行的速度会得到很大提升。

不仅如此，优化后的代码在去求所有解时，不会求出重复情况。

拓展：获得所有解（不重复）

求所有解的代码在优化后的方法上，简单调整以下就好

  • 不再返回（即不会试到一个成功的就退出）
  • 成功后将结果记录，记录时要使用切片进行拷贝。

首先，先在NQueens的__init__方法中添加新的属性，用于记录解决方法。

self.solutions = []

然后给NQueens类添加新方法solve_all

def solve_all(self, ri=0):

    for ci in range(self.n):

        if self.check_can_place(ri, ci):

            pos = (ci, ri)

            self.one_solution.append(pos)

            if ri == self.n - 1:

                self.solutions.append(self.one_solution[:])

            else:

                self.solve_all(ri+1)

            self.one_solution.pop()

然后修改下show_in_board方法。

因为原来的方法只能展示self.one_solution。

这里希望也能够展示别的solution

修改后的show_in_board如下

def show_in_board(self, sol=None):

    board = [

        ["-" for i in range(self.n)] for j in range(self.n)

    ]

    if sol is None:

        sol = self.one_solution

    for pos in sol:

        pc, pr = pos

        board[pr][pc] = "Q"

    for row in board:

        print(" ".join(row))

总代码

一个NQueens的实例，只能调用三个方法中的一个(一次)

  • solve
  • solve_advanced
  • solve_all

重复调用可能会出问题（需要再调用，建议新建NQueens实例）

以下总代码中只展示solve_all的调用结果。

且由于八皇后问题的解太多(有92个)，

以下只展示下六皇后问题的调用求解

class NQueens:

    def __init__(self, n):

        self.n = n

        # 保存每个皇后的坐标, (ci, ri)

        # 第一行第一列的皇后坐标为(0, 0)

        self.one_solution = []

        self.solutions = [

        ]

    def check_can_place(self, ri, ci):

        for pos in self.one_solution:

            pc, pr = pos

            if pc == ci:  # 行检测

                return False

            if pr == ri:  # 列检测

                return False

            if pr - pc == ri - ci:  # 对角线检测 1

                return False

            if pr + pc == ri + ci:  # 对角线检测 2

                return False

        return True

    def solve(self):

        for ri in range(self.n):

            for ci in range(self.n):

                if self.check_can_place(ri, ci):

                    pos = (ci, ri)

                    self.one_solution.append(pos)

                    if len(self.one_solution) == self.n:

                        return True

                    res = self.solve()

                    if res:

                        return True

                    else:

                        self.one_solution.pop()

        return False

    def solve_advanced(self, ri=0):

        for ci in range(self.n):

            if self.check_can_place(ri, ci):

                pos = (ci, ri)

                self.one_solution.append(pos)

                if ri == self.n - 1:

                    return True

                res = self.solve_advanced(ri+1)

                if res:

                    return True

                else:

                    self.one_solution.pop()

        return False

    def solve_all(self, ri=0):

        for ci in range(self.n):

            if self.check_can_place(ri, ci):

                pos = (ci, ri)

                self.one_solution.append(pos)

                if ri == self.n - 1:

                    self.solutions.append(self.one_solution[:])

                else:

                    self.solve_all(ri+1)

                self.one_solution.pop()

    def show_in_board(self, sol=None):

        board = [

            ["-" for i in range(self.n)] for j in range(self.n)

        ]

        if sol is None:

            sol = self.one_solution

        for pos in sol:

            pc, pr = pos

            board[pr][pc] = "Q"

        for row in board:

            print(" ".join(row))

nq = NQueens(6)

solutions = nq.solve_all()

for si in range(len(nq.solutions)):

    sol = nq.solutions[si]

    print("=== Solution %s ===" % si)

    print("Queens positions:")

    print(sol)

    print("Queens in board:")

    nq.show_in_board(sol)

输出

总代码的输出如下

=== Solution 0 ===

Queens positions:

[(1, 0), (3, 1), (5, 2), (0, 3), (2, 4), (4, 5)]

Queens in board:

- Q - - - -

- - - Q - -

- - - - - Q

Q - - - - -

- - Q - - -

- - - - Q -

=== Solution 1 ===

Queens positions:

[(2, 0), (5, 1), (1, 2), (4, 3), (0, 4), (3, 5)]

Queens in board:

- - Q - - -

- - - - - Q

- Q - - - -

- - - - Q -

Q - - - - -

- - - Q - -

=== Solution 2 ===

Queens positions:

[(3, 0), (0, 1), (4, 2), (1, 3), (5, 4), (2, 5)]

Queens in board:

- - - Q - -

Q - - - - -

- - - - Q -

- Q - - - -

- - - - - Q

- - Q - - -

=== Solution 3 ===

Queens positions:

[(4, 0), (2, 1), (0, 2), (5, 3), (3, 4), (1, 5)]

Queens in board:

- - - - Q -

- - Q - - -

Q - - - - -

- - - - - Q

- - - Q - -

- Q - - - -

参考文档

【大爽python算法】递归算法进化之回溯算法(backtracking)的更多相关文章

  1. 大爽Python入门教程 2-3 字符串，列表，字典

    大爽Python入门公开课教案 点击查看教程总目录 除了通用的序列方法, 列表和字符串还有些自己的专属方法. 后面介绍有些是英中文对照介绍(英文来自官方文档), 便于大家更深入的去理解其意思. 灵活的 ...

  2. 大爽Python入门教程 3-3 循环：`for`、`while`

    大爽Python入门公开课教案 点击查看教程总目录 for循环 可迭代对象iterable 不同于其他语言. python的for循环只能用于遍历 可迭代对象iterable 的项. 即只支持以下语法 ...

  3. 大爽Python入门教程 3-4 实践例题

    大爽Python入门公开课教案 点击查看教程总目录 1. 求和 使用循环,计算列表所有项的和,并输出这个和. 列表示例 lst = [8, 5, 7, 12, 19, 21, 10, 3, 2, 11 ...

  4. 大爽Python入门教程 3-5 习题

    大爽Python入门公开课教案 点击查看教程总目录 1 求平方和 使用循环,计算列表所有项的平方和,并输出这个和. 列表示例 lst = [8, 5, 7, 12, 19, 21, 10, 3, 2, ...

  5. 大爽Python入门教程 3-6 答案

    大爽Python入门公开课教案 点击查看教程总目录 1 求平方和 使用循环,计算列表所有项的平方和,并输出这个和. 列表示例 lst = [8, 5, 7, 12, 19, 21, 10, 3, 2, ...

  6. 大爽Python入门教程 2-5 *拓展实践，对比与思考

    大爽Python入门公开课教案 点击查看教程总目录 本文偏难. 推荐等第一二三四章上完后,回过来拓展阅读. 基础情景思考 假设有这样一张成绩表 最左边的一列是名字,起名麻烦. 这里直接用ABC...来 ...

  7. 大爽Python入门教程 3-1 布尔值: True, False

    大爽Python入门公开课教案 点击查看教程总目录 1 布尔值介绍 从判断说起 回顾第一章介绍的简单的判断 >>> x = 10 >>> if x > 5: ...

  8. 大爽Python入门教程 3-2 条件判断: if...elif..else

    大爽Python入门公开课教案 点击查看教程总目录 简单回顾if 回顾下第一章的代码 >>> x = 5 >>> if x > 0: ... print(&q ...

  9. 大爽Python入门教程 总目录

    作者自我介绍:b站小UP主,时常直播编程+红警三,python1对1辅导老师. 大爽Python入门公开课教案 本篇博客为公开课教案目录,正文内容在目录章节链接的博客里 除目录本身外,没有链接的章节, ...

随机推荐

  1. Spirit带你彻底搞懂JS的6种继承方案

    JavaScript中实现继承的6种方案 01-原型链的继承方案 function Person(){ this.name="czx"; } function Student(){ ...

  2. Windows下Vim插件管理器Vundle的安装以及使用简介

    Vundle下载 从GitHub clone仓库 cd %USERPROFILE% git clone git@github.com:VundleVim/Vundle.vim.git %USERPRO ...

  3. 转载 使用wce进行本地和域的hash注入

    参数解释:-l 列出登录的会话和NTLM凭据(默认值)-s 修改当前登录会话的NTLM凭据 参数:<用户名>:<域名>:<LM哈希>:<NT哈希>-r ...

  4. 移动端多个DIV简单拖拽功能

    移动端多个DIV简单拖拽功能. 这个demo与之前写的一个例子差不了多少,只是这个多了一层遍历而已. <!DOCTYPE html> <html lang="en" ...

  5. 在开源项目或项目中使用git建立fork仓库

    前言: vector我们经常使用,对vector里面的基本函数构造函数.增加函数.删除函数.遍历函数我们也会用到.其中在使用遍历之后erase删除元素过程中,会出现一种删除最后一个元素破坏了迭代器的情 ...

  6. c++ fstream feekg讨论

    #include <iostream> #include <fstream> using namespace std; int main() { std::ifstream f ...

  7. bzoj4552排序（线段树，二分）

    题目大意 给定一个长度为n的序列,有m个操作,操作包括两种: \(0\ l\ r\)区间[l,r]的数字升序排序 \(1\ l\ r\)区间[l,r]的数字降序排序 最后询问在q位置上的数是多少? 其 ...

  8. Spring框架访问数据库的两种方式的小案例

    1.1 以Xml的方式访问数据库的案例 要以xml的方式访问数据库需要用到JdbcTemplate ,因为 JdbcTemplate(jdbc的模板对象)在Spring 中提供了一个可以操作数据库的对 ...

  9. 分布式系统ID

    Leaf--美团点评分布式ID生成系统 前言 在复杂分布式系统中,往往需要对大量的数据和消息进行唯一标识.如在美团点评的金融.支付.餐饮.酒店.猫眼电影等产品的系统中,数据日渐增长,对数据分库分表后需 ...

  10. eclipse javase版安装插件开发web项目

    最近学习开发javaweb,但是安装的却是java se版的eclipse,但其无法新建web项目,即找不到Dynamic Web.所以需要下载相应插件.以下为操作过程. 1. 在联网的情况下,打开e ...