A Unified Deep Model of Learning from both Data and Queries for Cardinality Estimation 论文解读（SIGMOD 2021）

A Unified Deep Model of Learning from both Data and Queries for Cardinality Estimation 论文解读（SIGMOD 2021）

• 本篇博客是对A Unified Deep Model of Learning from both Data and Queries for Cardinality Estimation的一些重要idea的解读，原文连接为：A Unified Deep Model of Learning from both Data and Queries for Cardinality Estimation (acm.org)
• 该文重点介绍了同时从data和query中学习联合数据分布的方法。
• 特点：
  • 不做任何独立性假设
  • 同时利用data和query训练模型
  • 增量更新，更好的时间和空间消耗

基数估计及联合分布相关信息

• 该部分在笔者另一篇介绍Naru的博客中已经讲述Deep Upsupervised Cardinality Estimation 解读（2019 VLDB） - 茶柒每天要学习 - 博客园 (cnblogs.com) 这里不做过多赘述，本文所用到的模型在data-driven方面的思想与Naru基本一致（包括使用自回归模型，encoding，decoding，progressive sampling）下文的重点是介绍如何用query（监督数据）训练data-driven（无监督模型）。

在自回归模型中加入query信息训练的challenge

现有的自回归模型无法实现从query中学习，这是因为在做反向传播时，梯度无法流经采样的一些离散随机变量（在本文中代表进行范围查询时渐进采样出的一系列点），因此采样过程是不可微的。本文介绍了使用gumbel-softmax方法对采样的点进行重参数化，使之可微的方法。

Gumbel-Softmax Trick

• gumbel-softmax是一种重参数化技巧，假设我们知道数据表中某一个属性列的概率分布P，范围查询需要我们在目标范围按照该概率分布采样出一些点{x...}，利用这些采样点对范围选择度进行估计。但是这样采样出来的点有一个问题：x只是按照某种概率分布P直接选择出来的值，并没有一个明确定义公式，这就导致了x虽然与概率P存在某种关联，但是并没有办法对其进行求导，也就不能利用反向传播调整概率分布。
• 既然问题的原因是没有一个明确的公式，那么我们构造出一个公式，使之得到的结果就是这些采样不就可以解决不可微的问题了吗？我们想要构造的就是下式，即gumbel-max技巧：

\[f(x)=\left\{ \begin{aligned} 1,i=argmax(log(p_j)+g_j) \\0,otherwisee \end{aligned} \right.
\]

其中\(g_i=-log(-log(u_i)),u_i\sim Uniform(0,1)\).被称为Gumbel噪声，这个噪声的作用是使得每次公式产生的结果都不一致因为如果每次都一致就不叫采样了。根据该式我们最终会得到一个one-hot向量，用该向量与待采样的值域空间相乘即可得到采样点。我们注意到上式存在argmax操作，该操作也是不可微的，此时我们用softmax操作代替argmax即可解决问题，而最终方案被称为gumbel-softmax技巧。

损失函数

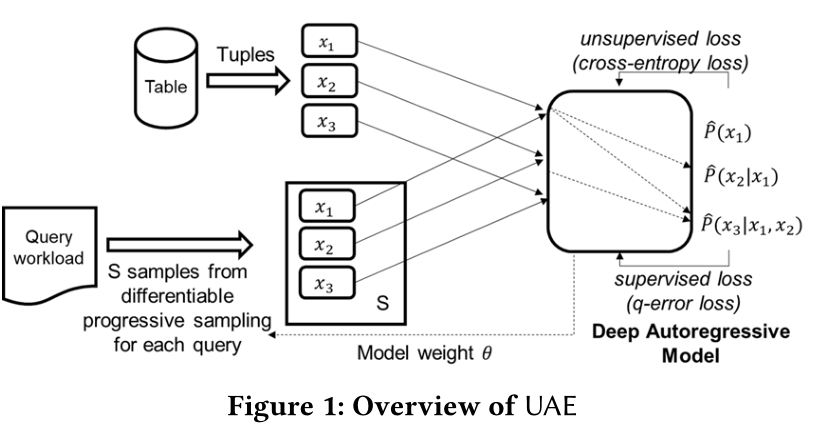
• data-driven 使用交叉熵损失函数
• query-driven使用q-error 损失函数*
• 本文通过一个超参数将两者相结合如下图：
  
  

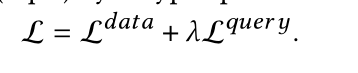
workflow