ACwing1212. 地宫取宝

题目:

X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是 k 件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 k 件宝贝。

输入格式:

第一行 3 个整数，n,m,k，含义见题目描述。

接下来 n 行，每行有 m 个整数 Ci 用来描述宝库矩阵每个格子的宝贝价值。

输出格式:

输出一个整数，表示正好取 k 个宝贝的行动方案数。

该数字可能很大，输出它对 1000000007 取模的结果。

数据范围:

\[1≤n,m≤50,
1≤k≤12,
0≤Ci≤12
\]

输入样例1：

2 2 2
1 2
2 1

输出样例1：

2

输入样例2：

2 3 2
1 2 3
2 1 5

输出样例2：

14

思路:

从题目分析来看、这个题是典型的摘花生问题和最长上升子序列问题的一个结合版、通过闫氏DP分析法、分析图如下所示。

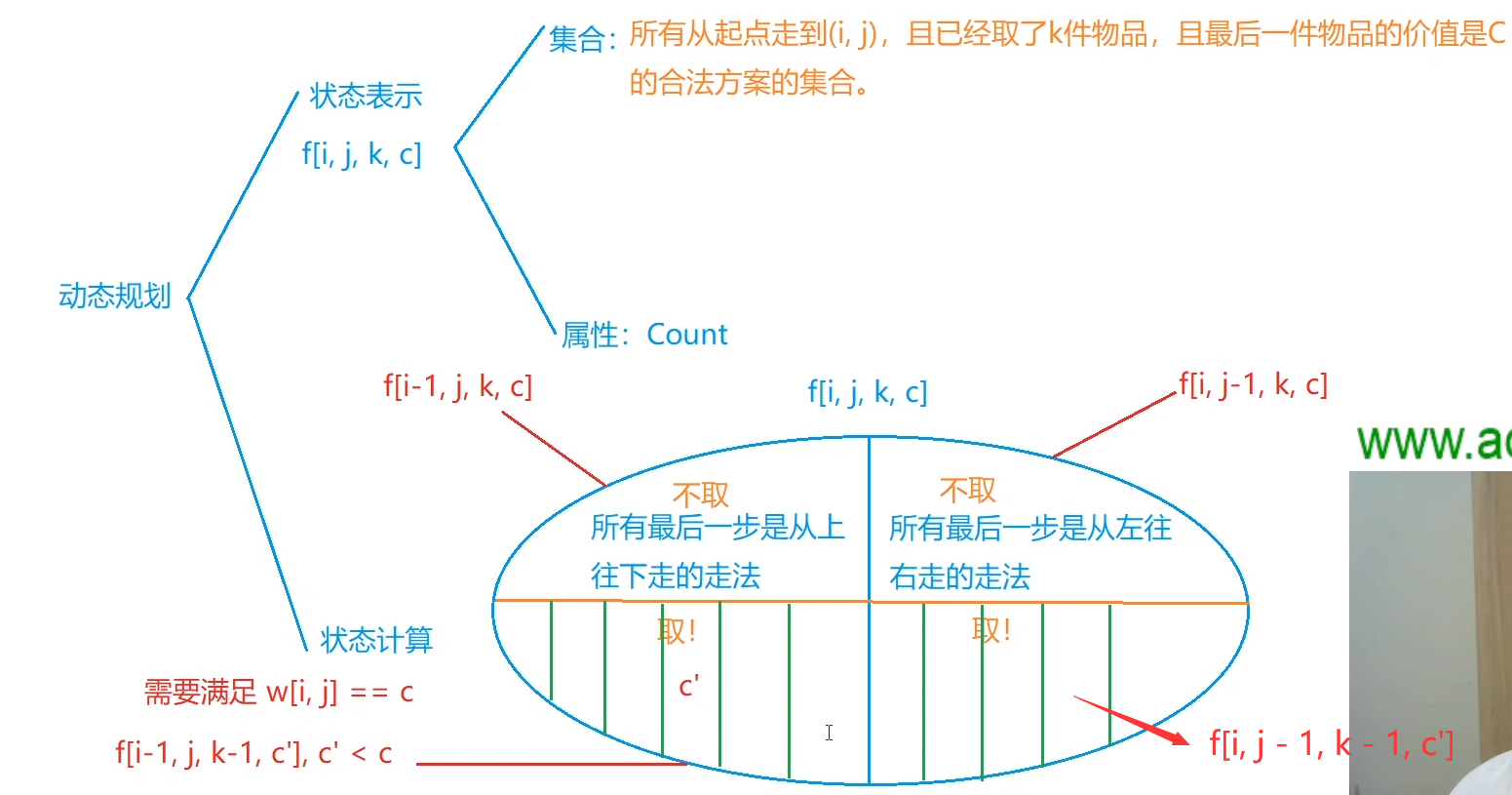
简单解释一下、不取的方案比较容易想到、取的时候、必须要满足w[i][j] == c这个条件、因为取完之后、最后一个值也就是最大的值、必须要满足w[i][j] == c才可以开始取。如果满足这个条件之后、具体的值又是多少呢？f[i - 1][j][k - 1][c']此时我取了这种方案、那取之前呢、对应的位置就是k - 1。该题解待补充.....

代码:

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 55, MOD = 1000000007;
int n, m, k;
int w[N][N];
int f[N][N][13][14];

int main()
{
    cin >> n >> m >> k;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = 1; j <= m ;j ++)
        {
            cin >> w[i][j];
            w[i][j] ++;
        }

    f[1][1][1][w[1][1]] = 1;    //初始化
    f[1][1][0][0] = 1;

    for(int i = 1; i <= n ; i ++)
    {
        for(int j = 1; j <= m ; j ++)
        {
            if(i == 1 && j == 1) continue;
            for(int u = 0 ; u <= k ; u ++)
                for(int v = 0 ; v <= 13 ; v ++)
                {
                    int &val = f[i][j][u][v];   // 取引用方便操作
                    val = (val + f[i - 1][j][u][v]) % MOD;  //每次操作两维、防止爆int
                    val = (val + f[i][j - 1][u][v]) % MOD;
                    if(v > 0 && v == w[i][j])   // 如果当前v大于零并且等于w[i][j]
                    {
                        for(int c = 0; c < v ; c ++)
                        {
                            val = (val + f[i - 1][j][u - 1][c]) % MOD;
                            val = (val + f[i][j - 1][u - 1][c]) % MOD;
                        }
                    }
                }
        }
    }

    int res = 0 ;
    for(int i = 0 ; i <= 13 ; i ++) res = (res + f[n][m][k][i]) % MOD;  // 统计所有方案

    cout << res << endl;
    return 0;
}