二叉搜索树(Binary Search Tree)(Java实现)
@
1、二叉搜索树
1.1、 基本概念
二叉树的一个性质是一棵平均二叉树的深度要比节点个数N小得多。分析表明其平均深度为\(\mathcal{O}(\sqrt{N})\),而对于特殊类型的二叉树,即二叉查找树(binary search tree),其深度的平均值为\(\mathcal{O}(log N)\)。
二叉查找树的性质: 对于树中的每个节点X,它的左子树中所有项的值小于X中的项,而它的右子树中所有项的值大于X中的项。
由于树的递归定义,通常是递归地编写那些操作的例程。因为二叉查找树的平均深度为\(\mathcal{O}(log N)\),所以一般不必担心栈空间被用尽。
1.2、树的节点(BinaryNode)
二叉查找树要求所有的项都能够排序,有两种实现方式;
- 对象实现接口 Comparable, 树中的两项使用compareTo方法进行比较;
- 使用一个函数对象,在构造器中传入一个比较器;
本篇文章采用了构造器重载,并定义了myCompare方法,使用了泛型,因此两种方式都支持,在后续的代码实现中可以看到。
节点定义:
/**
* 节点
*
* @param <AnyType>
*/
private static class BinaryNode<AnyType> {
BinaryNode(AnyType theElement) {
this(theElement, null, null);
}
BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) {
element = theElement;
left = left;
right = right;
}
AnyType element; // the data in the node
BinaryNode<AnyType> left; // Left child
BinaryNode<AnyType> right; // Right child
}
1.3、构造器和成员变量
private BinaryNode<AnyType> root;
private Comparator<? super AnyType> cmp;
/**
* 无参构造器
*/
public BinarySearchTree() {
this(null);
}
/**
* 带参构造器,比较器
*
* @param c 比较器
*/
public BinarySearchTree(Comparator<? super AnyType> c) {
root = null;
cmp = c;
}
关于比较器的知识可以参考下面这篇文章:
Java中Comparator的使用
关于泛型的知识可以参考下面这篇文章:
如何理解 Java 中的 <T extends Comparable<? super T>>
1.3、公共方法(public method)
主要包括插入,删除,找到最大值、最小值,清空树,查看元素是否包含;
/**
* 清空树
*/
public void makeEmpty() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
public boolean contains(AnyType x){
return contains(x,root);
}
public AnyType findMin(){
if (isEmpty()) throw new BufferUnderflowException();
return findMin(root).element;
}
public AnyType findMax(){
if (isEmpty()) throw new BufferUnderflowException();
return findMax(root).element;
}
public void insert(AnyType x){
root = insert(x, root);
}
public void remove(AnyType x){
root = remove(x,root);
}
1.4、比较函数
如果有比较器,就使用比较器,否则要求对象实现了Comparable接口;
private int myCompare(AnyType lhs, AnyType rhs) {
if (cmp != null) {
return cmp.compare(lhs, rhs);
} else {
return lhs.compareTo(rhs);
}
}
1.5、contains 函数
本质就是一个树的遍历;
private boolean contains(AnyType x, BinaryNode<AnyType> t) {
if (t == null) {
return false;
}
int compareResult = myCompare(x, t.element);
if (compareResult < 0) {
return contains(x, t.left);
} else if (compareResult > 0) {
return contains(x, t.right);
} else {
return true;
}
}
1.6、findMin
因为二叉搜索树的性质,最小值一定是树的最左节点,要注意树为空的情况。
/**
* Internal method to find the smallest item in a subtree
* @param t the node that roots the subtree
* @return node containing the smallest item
*/
private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
if (t == null) {
return null;
}
if (t.left == null) {
return t;
}
return findMin(t.left);
}
1.7、findMax
最右节点;
/**
* Internal method to find the largest item in a subtree
* @param t the node that roots the subtree
* @return the node containing the largest item
*/
private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){
if (t == null){
return null;
}
if (t.right == null){
return t;
}
return findMax(t.right);
}
1.8、insert
这个主要是根据二叉搜索树的性质,注意当树为空的情况,就可以加入新的节点了,还有当该值已经存在时,默认不进行操作;
/**
* Internal method to insert into a subtree
* @param x the item to insert
* @param t the node that roots the subtree
* @return the new root of the subtree
*/
private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){
if (t == null){
return new BinaryNode<>(x,null,null);
}
int compareResult = myCompare(x,t.element);
if (compareResult < 0){
t.left = insert(x,t.left);
}
else if (compareResult > 0){
t.right = insert(x,t.right);
}
else{
//Duplicate; do nothing
}
return t;
}
1.9、remove

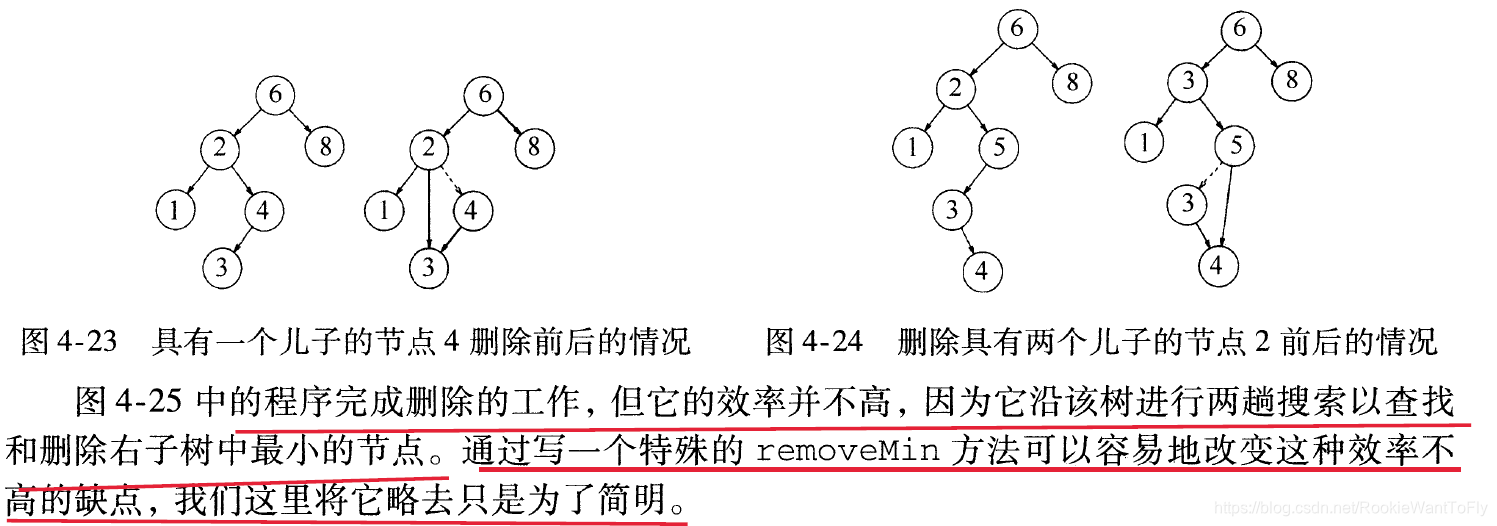

注意当空树时,返回null;
最后一个三元表达式,是在之前已经排除掉节点有两个儿子的情况下使用的。
/**
* Internal method to remove from a subtree
* @param x the item to remove
* @param t the node that roots the subtree
* @return the new root of the subtree
*/
private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){
if (t == null){
return t; // Item not found ,do nothing
}
int compareResult = myCompare(x,t.element);
if (compareResult < 0){
t.left = remove(x,t.left);
}
else if (compareResult > 0){
t.right = remove(x,t.right);
}
else if (t.left !=null && t.right!=null){
//Two children
t.element = findMin(t.right).element;
t.right = remove(t.element,t.right);
}
else
t = (t.left !=null) ? t.left:t.right;
return t;
}
二、完整代码实现(Java)
/**
* @author LongRookie
* @description: 二叉搜索树
* @date 2021/6/26 19:41
*/
import com.sun.source.tree.BinaryTree;
import java.nio.BufferUnderflowException;
import java.util.Comparator;
/**
* 二叉搜索树
*/
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {
/**
* 节点
*
* @param <AnyType>
*/
private static class BinaryNode<AnyType> {
BinaryNode(AnyType theElement) {
this(theElement, null, null);
}
BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) {
element = theElement;
left = left;
right = right;
}
AnyType element; // the data in the node
BinaryNode<AnyType> left; // Left child
BinaryNode<AnyType> right; // Right child
}
private BinaryNode<AnyType> root;
private Comparator<? super AnyType> cmp;
/**
* 无参构造器
*/
public BinarySearchTree() {
this(null);
}
/**
* 带参构造器,比较器
*
* @param c 比较器
*/
public BinarySearchTree(Comparator<? super AnyType> c) {
root = null;
cmp = c;
}
/**
* 清空树
*/
public void makeEmpty() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
public boolean contains(AnyType x){
return contains(x,root);
}
public AnyType findMin(){
if (isEmpty()) throw new BufferUnderflowException();
return findMin(root).element;
}
public AnyType findMax(){
if (isEmpty()) throw new BufferUnderflowException();
return findMax(root).element;
}
public void insert(AnyType x){
root = insert(x, root);
}
public void remove(AnyType x){
root = remove(x,root);
}
private int myCompare(AnyType lhs, AnyType rhs) {
if (cmp != null) {
return cmp.compare(lhs, rhs);
} else {
return lhs.compareTo(rhs);
}
}
private boolean contains(AnyType x, BinaryNode<AnyType> t) {
if (t == null) {
return false;
}
int compareResult = myCompare(x, t.element);
if (compareResult < 0) {
return contains(x, t.left);
} else if (compareResult > 0) {
return contains(x, t.right);
} else {
return true;
}
}
/**
* Internal method to find the smallest item in a subtree
* @param t the node that roots the subtree
* @return node containing the smallest item
*/
private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
if (t == null) {
return null;
}
if (t.left == null) {
return t;
}
return findMin(t.left);
}
/**
* Internal method to find the largest item in a subtree
* @param t the node that roots the subtree
* @return the node containing the largest item
*/
private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){
if (t == null){
return null;
}
if (t.right == null){
return t;
}
return findMax(t.right);
}
/**
* Internal method to remove from a subtree
* @param x the item to remove
* @param t the node that roots the subtree
* @return the new root of the subtree
*/
private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){
if (t == null){
return t; // Item not found ,do nothing
}
int compareResult = myCompare(x,t.element);
if (compareResult < 0){
t.left = remove(x,t.left);
}
else if (compareResult > 0){
t.right = remove(x,t.right);
}
else if (t.left !=null && t.right!=null){
//Two children
t.element = findMin(t.right).element;
t.right = remove(t.element,t.right);
}
else
t = (t.left !=null) ? t.left:t.right;
return t;
}
/**
* Internal method to insert into a subtree
* @param x the item to insert
* @param t the node that roots the subtree
* @return the new root of the subtree
*/
private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){
if (t == null){
return new BinaryNode<>(x,null,null);
}
int compareResult = myCompare(x,t.element);
if (compareResult < 0){
t.left = insert(x,t.left);
}
else if (compareResult > 0){
t.right = insert(x,t.right);
}
else{
//Duplicate; do nothing
}
return t;
}
}
二叉搜索树(Binary Search Tree)(Java实现)的更多相关文章
- 编程算法 - 二叉搜索树(binary search tree) 代码(C)
二叉搜索树(binary search tree) 代码(C) 本文地址: http://blog.csdn.net/caroline_wendy 二叉搜索树(binary search tree)能 ...
- 数据结构 《5》----二叉搜索树 ( Binary Search Tree )
二叉树的一个重要应用就是查找. 二叉搜索树 满足如下的性质: 左子树的关键字 < 节点的关键字 < 右子树的关键字 1. Find(x) 有了上述的性质后,我们就可以像二分查找那样查找给定 ...
- [Data Structure] 二叉搜索树(Binary Search Tree) - 笔记
1. 二叉搜索树,可以用作字典,或者优先队列. 2. 根节点 root 是树结构里面唯一一个其父节点为空的节点. 3. 二叉树搜索树的属性: 假设 x 是二叉搜索树的一个节点.如果 y 是 x 左子树 ...
- 二叉搜索树(Binary Search Tree)实现及测试
转:http://blog.csdn.net/a19881029/article/details/24379339 实现代码: Node.java //节点类public class Node{ ...
- 数据结构之Binary Search Tree (Java)
二叉查找树简介 二叉查找树(Binary Search Tree), 也成二叉搜索树.有序二叉树(ordered binary tree).排序二叉树(sorted binary tree), 是指一 ...
- leetcode 98 Validate Binary Search Tree ----- java
Given a binary tree, determine if it is a valid binary search tree (BST). Assume a BST is defined as ...
- 二叉搜索树详解(Java实现)
1.二叉搜索树定义 二叉搜索树,是指一棵空树或者具有下列性质的二叉树: 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值: 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根 ...
- 剑指Offer-26.二叉搜索树与双向链表(C++/Java)
题目: 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表.要求不能创建任何新的结点,只能调整树中结点指针的指向. 分析: 创建两个指针,分别指向要处理的当前元素和当前元素的前一个元素.利用中 ...
- leetcode 99 Recover Binary Search Tree ----- java
Two elements of a binary search tree (BST) are swapped by mistake. Recover the tree without changing ...
随机推荐
- 用nvm的方式安装node
一.nvm简介 Node Version Manager(Node版本管理工具)由于以后的开发工作可能会在多个Node版本中测试,而且Node的版本也比较多,所以需要这么款工具来管理. nvm的安 ...
- 7.6 passwd:修改用户密码
7.6 passwd:修改用户密码 passwd命令可以修改用户密码及密码过期时间等内容,是工作中很常用的命令.普通用户和超级用户都可以运行passwd命令,但普通用户只能更改自身的用户密码, ...
- Swift系列十 - inout的本质
inout是可以用来在函数内部修改外部属性内存的. 一.inout回顾 示例代码: func test(_ num: inout Int) { num = 20 } var a = 10 test(& ...
- 大数据学习之路——环境配置(2)——mysql 在linux 系统上安装配置
1.安装参考网址: https://blog.csdn.net/IronWring_Fly/article/details/103637801 设置新秘密: mysqladmin -u root ...
- python使用多线程备份数据库
前言:在日常服务器运维工作中,备份数据库是必不可少的,刚工作那会看到公司都是用shell脚本循环备份数据库,到现在自己学习python语言后,利用多进程多线程相关技术来实现并行备份数据库,充分利用服务 ...
- linux上传启动项目命令
使用Xshell 或其他远程链接登录工具登录服务器后 1.切换用户到root: sudo -i 账户密码 注意:可直接将jar包放入root用户目录下,避免有可能因为服务器文件夹权限设置导致在指定文件 ...
- uni-app 富文本解析-小程序
原文:http://www.upwqy.com/manual/info/105.html 1 引入插件 gaoyia-parse 链接:https://pan.baidu.com/s/1UusfXxH ...
- 使用Python操作InfluxDB时序数据库
使用Python操作InfluxDB时序数据库 安装python包 influxdb,这里我安装的是5.3.0版本 pip install influxdb==5.3.0 使用 from infl ...
- python3操作Kafka
# -- coding: UTF-8 import datetime import json import time from kafka import KafkaProducer producer= ...
- TensorFlow之keras.layers.Conv2D( )
keras.layers.Conv2D( ) 函数参数 def __init__(self, filters, kernel_size, strides=(1, 1), padding='valid' ...
