手把手教你 Docker Compose的安装和使用

一、Docker Compose是什么？

1. Docker Compose是一个工具，用于定义和运行多容器应用程序的工具；
2. Docker Compose通过yml文件定义多容器的docker应用；
3. Docker Compose通过一条命令根据yml文件的定义去创建或管理多容器；
4. Docker Compose是用来做Docker的多容器控制，是一个用来把Docker自动化的东西。有了Docker Compose你可以把所有繁复的 Docker 操作全都一条命令，自动化的完成（可以简单理解为批处理）。

二、Docker Compose安装步骤

1、下载Docker Compose二进制文件，我这里下载的版本是1.29.2

sudo curl -L "https://github.com/docker/compose/releases/download/1.29.2/docker-compose-$(uname -s)-$(uname -m)" -o /usr/local/bin/docker-compose

2、对刚刚下载的二进制文件添加可执行权限

sudo chmod +x /usr/local/bin/docker-compose

3、通过docker-compose --version命令检查是否安装成功

三、Docker Compose版本差别

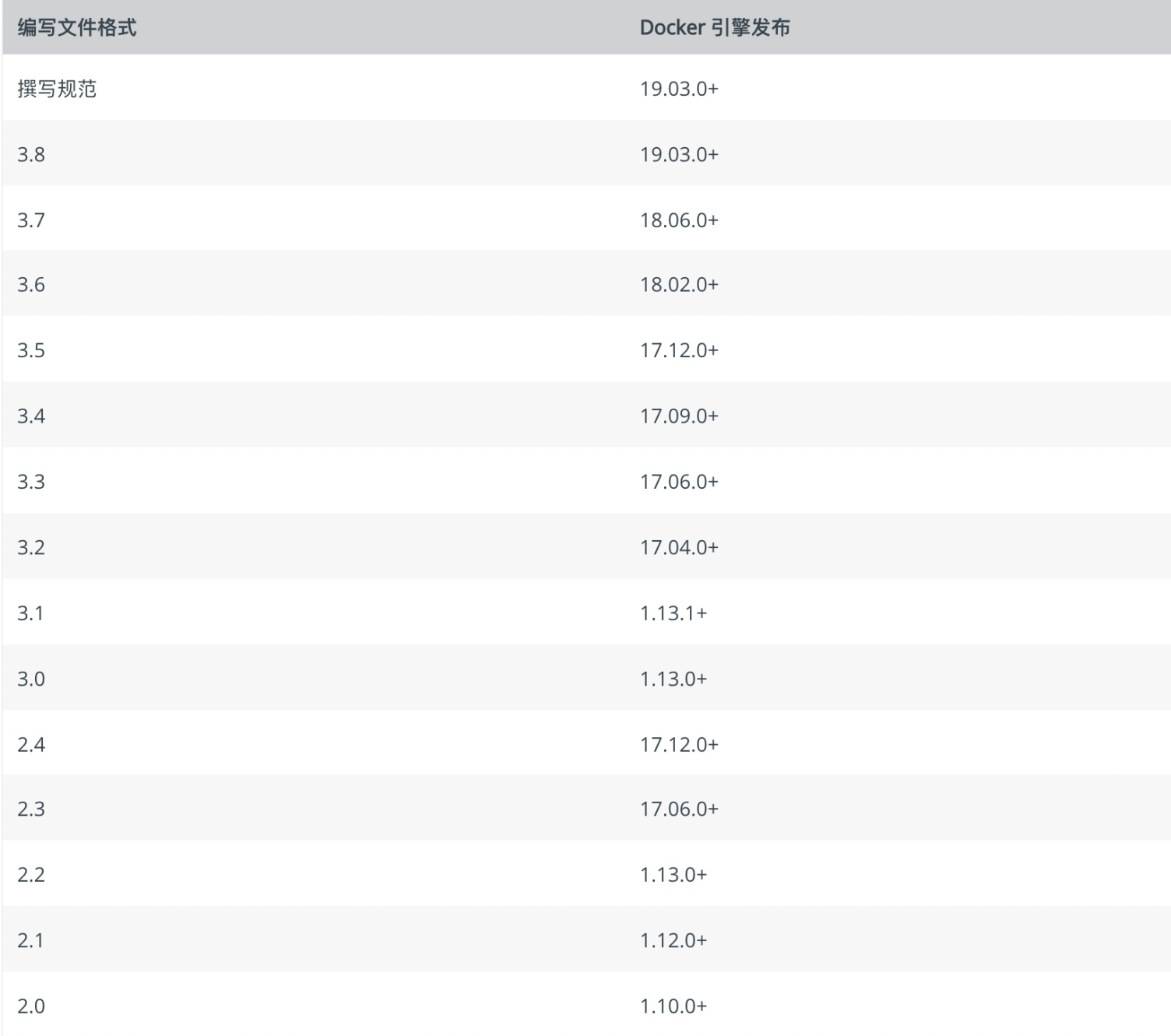
1. v3 版本不支持 volume_from 、extends、group_add等属性;
2. cpu 和 内存属性的设置移到了 deploy 中;
3. v3 版本支持 Docker Swarm，而 v2 版本不支持;

注意：官方目前在 1.20.0 引入了一个新--compatibility标志，帮助开发人员轻松的过渡到v3，目前还有些问题官方还不建议直接使用到生产，建议大家直接上手v3版本。

四、Docker Compose基本命令

Docker Compose命令基本上和Docker相差不多，主要就是对Docker Compose生命周期控制、日志格式等相关命令，可以通过docker-compose --help查看帮助。

#构建启动nignx容器
docker-compose up -d nginx                     

#进入nginx容器中
docker-compose exec nginx bash            

#将会停止UP命令启动的容器，并删除容器
docker-compose down                             

#显示所有容器
docker-compose ps                                   

#重新启动nginx容器
docker-compose restart nginx                   

#构建nginx镜像
docker-compose build nginx      

#不带缓存的构建nginx镜像
docker-compose build --no-cache nginx 

#查看nginx的日志
docker-compose logs  nginx                      

#查看nginx的实时日志
docker-compose logs -f nginx                   

#验证（docker-compose.yml）文件配置，
#当配置正确时，不输出任何内容，当文件配置错误，输出错误信息
docker-compose config  -q                        

#以json的形式输出nginx的docker日志
docker-compose events --json nginx       

#暂停nignx容器
docker-compose pause nginx                 

#恢复ningx容器
docker-compose unpause nginx             

#删除nginx容器
docker-compose rm nginx                       

#停止nignx容器
docker-compose stop nginx                    

#启动nignx容器
docker-compose start nginx

五、使用案例请查看《手把手教你 Docker搭建gitlab社区汉化版》