Codeforces Round #365 (Div. 2) D 树状数组+离线处理

D. Mishka and Interesting sum

time limit per test

3.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Mishka enjoys programming. Since her birthday has just passed, her friends decided to present her with array of non-negative integers a1, a2, ..., an of n elements!

Mishka loved the array and she instantly decided to determine its beauty value, but she is too little and can't process large arrays. Right because of that she invited you to visit her and asked you to process m queries.

Each query is processed in the following way:

1. Two integers l and r (1 ≤ l ≤ r ≤ n) are specified — bounds of query segment.
2. Integers, presented in array segment [l,  r] (in sequence of integers al, al + 1, ..., ar) even number of times, are written down.
3. XOR-sum of written down integers is calculated, and this value is the answer for a query. Formally, if integers written down in point 2 are x1, x2, ..., xk, then Mishka wants to know the value , where  — operator of exclusive bitwise OR.

Since only the little bears know the definition of array beauty, all you are to do is to answer each of queries presented.

Input

The first line of the input contains single integer n (1 ≤ n ≤ 1 000 000) — the number of elements in the array.

The second line of the input contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — array elements.

The third line of the input contains single integer m (1 ≤ m ≤ 1 000 000) — the number of queries.

Each of the next m lines describes corresponding query by a pair of integers l and r (1 ≤ l ≤ r ≤ n) — the bounds of query segment.

Output

Print m non-negative integers — the answers for the queries in the order they appear in the input.

Examples

input

3
3 7 8
1
1 3

output

0

input

7
1 2 1 3 3 2 3
5
4 7
4 5
1 3
1 7
1 5

output

0
3
1
3
2

Note

In the second sample:

There is no integers in the segment of the first query, presented even number of times in the segment — the answer is 0.

In the second query there is only integer 3 is presented even number of times — the answer is 3.

In the third query only integer 1 is written down — the answer is 1.

In the fourth query all array elements are considered. Only 1 and 2 are presented there even number of times. The answer is .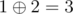

In the fifth query 1 and 3 are written down. The answer is .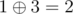

题意：给你n个数，m个区间询问 求区间出现次数为偶数次的数的异或和

题解：如果是奇数次呢？我们知道a^a=0 所以直接前缀异或和就可以处理。所以思考有没有一种反异或运算呢？自己模拟一遍发现这样是错误的。换一个思路考虑，将奇数次变为偶数次来处理，只需要计算出所要查询的区间内不同的数的异或和a 再 与这个区间的前缀异或和n做一次异或运算得到b，就能够将奇数次变为偶数次来处理（a^b=n可以得到b=a^n）,那么如何快速计算一个区间内不同的数的异或和呢？离线处理,结构体存储每个查询区间的左右边界，按照右边界排序，从左向右遍历序列 树状数组维护 不断的将数添加到树状数组，若当前位置的数存在前驱，则删除前驱 (删除就是再进行一次异或a^a=0) 对于共右边界的查询区间 一次遍历得到答案，然后继续遍历。

 /******************************
 code by drizzle
 blog: www.cnblogs.com/hsd-/
 ^ ^    ^ ^
  O      O
 ******************************/
 //#include<bits/stdc++.h>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<map>
 #include<algorithm>
 #include<queue>
 #include<cmath>
 #define ll __int64
 #define PI acos(-1.0)
 #define mod 1000000007
 using namespace std;
 int n,m;
 int a[];
 int sum[];
 int tree[];
 int re[];
 int pre[];
 map<int,int>mp;
 int lowbit(int t)
 {
     return t&(-t);
 }
 void add(int x,int y)
 {
     for(int i=x;i<=n;i+=lowbit(i))
         tree[i]=tree[i]^y;
 }
 int getsum(int x)
 {
     int ans=;
     for(int i=x;i>;i-=lowbit(i))
        ans^=tree[i];
     return ans;
 }
 struct node
 {
     int l,r;
     int pos;
 }N[];
 bool cmp(struct node aa,struct node bb)
 {
     return aa.r<bb.r;
 }
 int main()
 {
     scanf("%d",&n);
     sum[]=;
     mp.clear();
     for(int i=;i<=n;i++)
     {
         scanf("%d",&a[i]);
         sum[i]=sum[i-]^a[i];
         pre[i]=mp[a[i]];
         mp[a[i]]=i;
     }
     scanf("%d",&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d %d",&N[i].l,&N[i].r);
         N[i].pos=i;
     }
     sort(N+,N++m,cmp);
     int j=;
     for(int i=;i<=m;i++)
     {
         for(;j<=n&&j<=N[i].r;j++)
         {
             if(pre[j])
             add(pre[j],a[j]);
             add(j,a[j]);
         }
 re[N[i].pos]=sum[N[i].r]^sum[N[i].l-]^getsum(N[i].r)^getsum(N[i].l-);
     }
     for(int i=;i<=m;i++)
         printf("%d\n",re[i]);
     return ;
 }