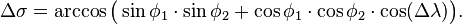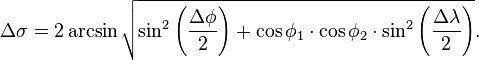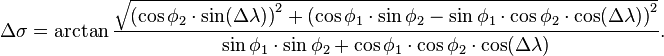C# JackLib系列之如何获取地球上两经纬度坐标点间的距离

获取地球上两经纬度坐标点间的距离，利用【大圆距离公式】

 

A diagram illustrating great-circle distance (drawn in red) between two points on a sphere, P and Q. Two antipodal points, u and v, are also depicted.

谷歌都在用呢， C#实现的代码如下：

 /// <summary>
 /// 地球半径
 /// </summary>
 private const double EARTH_RADIUS = 6378.137; 
 /// <summary>
 /// 获取两点之间的距离，大圆距离公式
 /// </summary>
 /// <param name="lat1"></param>
 /// <param name="lon1"></param>
 /// <param name="lat2"></param>
 /// <param name="lon2"></param>
 /// <returns></returns>
 public static double DistanceOfEarthTwoPoints(double latA, double lngA, double latB, double lngB) {   
     double radLat1 = lat1 * Math.PI / 180.0;
     double radLat2 = lat2 * Math.PI / 180.0;
     double a = radLat1 - radLat2;
     double b = lon1 * Math.PI / 180.0 - lon2 * Math.PI / 180.0;
     double s = 2 * Math.Asin(Math.Sqrt(Math.Pow(Math.Sin(a / 2), 2) + Math.Cos(radLat1) * Math.Cos(radLat2) * Math.Pow(Math.Sin(b / 2), 2)));
     s = s * EARTH_RADIUS;
     s = Math.Round(s * 1000000) / 1000000;
     return s;
 }

当然还有另一种写法：

/// <summary>
/// 获取两点之间的距离，大圆距离公式
/// </summary>
/// <param name="lat1"></param>
/// <param name="lon1"></param>
/// <param name="lat2"></param>
/// <param name="lon2"></param>
/// <returns></returns>
public static double DistanceOfEarthTwoPoints(double latA, double lngA, double latB, double lngB) {
   double s = Math.Acos(Math.Cos(Rad(latA)) * Math.Cos(Rad(latB)) * (Math.Cos(Rad(lngA) - Rad(lngB))) + Math.Sin(Rad(latA)) * Math.Sin(Rad(latB)));
   s = s * EARTH_RADIUS;
   s = Math.Round(s * ) / ;
   return s;
}

其实这两个方法是完全等价的，只是化简程序不同而已，看看下面的解释：

Formulas

 

An illustration of the central angle, Δσ, between two points, P and Q. λ and φ are the longitudinal and latitudinal angles of P respectively

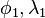Let and 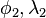be the geographical latitude and longitude of two points 1 and 2, and their absolute differences; then 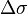, the central angle between them, is given by the spherical law of cosines:

The distance d, i.e. the arc length, for a sphere of radius r and 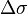given in radians

Computational formulas

On computer systems with low floating-point precision, the spherical law of cosines formula can have large rounding errors if the distance is small (if the two points are a kilometer apart on the surface of the Earth, the cosine of the central angle comes out 0.99999999). For modern 64-bit floating-point numbers, the spherical law of cosines formula, given above, does not have serious rounding errors for distances larger than a few meters on the surface of the Earth.^[2] The haversine formula is numerically better-conditioned for small distances:^[3]

Historically, the use of this formula was simplified by the availability of tables for the haversine function: hav(θ) = sin²(θ/2).

Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal points (on opposite ends of the sphere). A more complicated formula that is accurate for all distances is the following special case of the Vincenty formula for an ellipsoid with equal major and minor axes:^[4]

When programming a computer, one should use the atan2() function rather than the ordinary arctangent function (atan()), so that 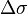is placed in the correct quadrant.

The determination of the great-circle distance is just part of the more general problem of great-circle navigation, which also computes the azimuths at the end points and intermediate way-points.