JS Leetcode 304. 二维区域和检索 - 矩阵不可变，彻底弄懂二维数组前缀和

壹 ❀ 引

我在JS LeetCode 303. 区域和检索 - 数组不可变，一维数组的前缀和一文中，记录了一维数组求区间合的解题思路，正好还有一题的升级版，题目来自leetcode304. 二维区域和检索 - 矩阵不可变，实不相瞒，我在看题解理解的过程中就花了不少时间，所以这里会写的格外详细一点，题目描述如下：

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例：

给定 matrix = [
 [3, 0, 1, 4, 2],
 [5, 6, 3, 2, 1],
 [1, 2, 0, 1, 5],
 [4, 1, 0, 1, 7],
 [1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

提示：

你可以假设矩阵不可变。

会多次调用 sumRegion 方法。

你可以假设 row1 ≤ row2 且 col1 ≤ col2 。

贰 ❀ 暴力解法

其实我在看此题的时候一开始就不理解为什么(row1, col1) = (2, 1)对应矩阵中的2，按照我们我们电影院找座位的习惯，应该是第二排的第一个才对，难道不是5？后来想到这里的矩阵其实是二维数组，数组索引起点是0，这才想明白对应的其实是第三排的第二个，因此左上角是2，右下角同理。

在前面一维数组前缀和的题解中，我们已经知道了如下公式（若不理解请先阅读一维数组前缀和题解）：

sumRange(i, j) = preSum[j + 1] - preSum[i]

那么站在本题的角度，我们是不是也可以分别求每行数组的前缀和，再根据区间差得到二维数组的区间和呢？我们从一个简单的二维数组开始理解，如下有二维数组[[1,1,1],[1,1,1],[1,1,1]]，我们需要求(1,1,2,2)的区域和：

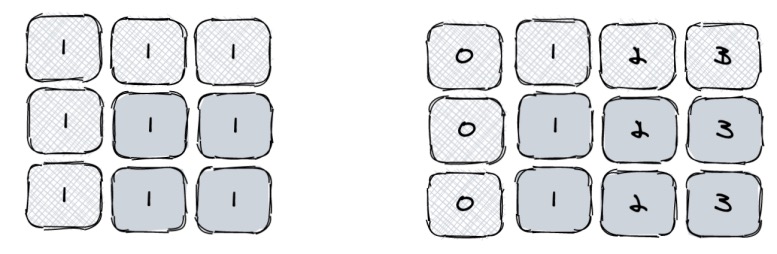
看图就知道答案是4，所以对应到右边的一维数组前缀和中，因为有两行数组，套公式应该是：

// 有两行，因此是两个sumRange相加
sumRange(1, 2) + sumRange(1, 2)
// 等同于
preSum[2 + 1] - preSum[1] + preSum[2 + 1] - preSum[1]
// 等同于
3 - 1 + 3 - 1 = 4

那么到这里你应该自己尝试实现具体的代码逻辑，下面是基于一维数组思路的暴力解法：

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function(matrix) {
    const preSums = [];
    for(let i =0;i<matrix.length;i++){
      	// 分别求每行数组的前缀和
        const preSum = new Array(matrix[i].length + 1);
      	// 为了让每位元素适用工时，将第0位设置为0是必要的
        preSum[0] = 0;
      	// 套用公式，唯一不同的是数组变成了二维，本质没什么区别
        for (let j = 1; j < preSum.length; j++) {
            preSum[j] = preSum[j-1]+matrix[i][j-1];
        };
        preSums.push(preSum);
    }
    this.preSums = preSums;
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
    // 从row1到row2行的前缀和都要加起来
    // 每行数组的前缀和符合一维数组前缀和公式，范围其实就是(col1,col2)
    // sumRange(i, j) = preSum[j + 1] - preSum[i]
    let sum = 0;
    for(let i = row1;i<=row2;i++){
        sum += this.preSums[i][col2 + 1] - this.preSums[i][col1];
    }
    return sum;
};

叁 ❀ 二维数组前缀和

前面介绍了比较暴力的做法，现在我们来介绍题目期望我们的做法，也就是套用二维数组前缀和的公式去解答，公式之前没听过不重要，现在你听过了。

我们假设O代表坐标（0，0），D代表坐标（i,j）结合图解，公式如下：

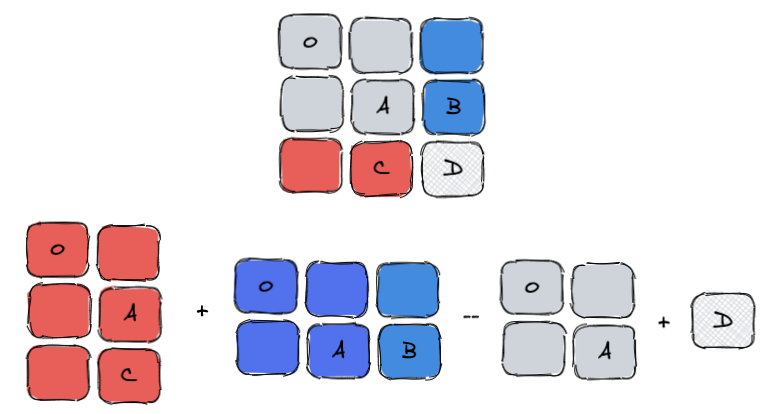
S(O,D)=S(O,C)+S(O,B)−S(O,A)+D

公式的意思是，0-->D的所有元素和，等于0-->C（红色6格）的所有元素和加上O-->B（蓝色6格）的所有元素和，再减去O-->A（灰色4格）的所有元素和，再加一个D（网状格）。

之所以减去一个O-->A是因为O-->C与O-->B两个重复了一次OA，因此得减去。

如果用preSum(i,j)来表示坐标（0,0）到（i,j）的左右元素和，以上公式等同于：

preSum[i][j] = preSum[i][j−1] + preSum[i−1][j] − preSum[i−1][j−1] + matrix[i][j]

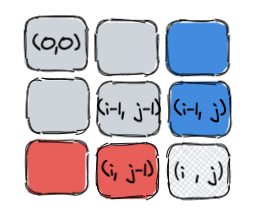
请结合上图来理解，说到底，preSum[i][j−1]就是S(O,C)，也就是前面图解中的红色区域，其它同理。而这个matrix[i][j]其实就是题目提供的数组matrix的第i行的第j个元素而已。

在我写这篇文章之前，我当时的第一直觉就是用一个简单的例子来验证这个公式对不对，但比较笨比的是我用了一维数组前缀和累加的思路验证公式，然后苦思冥想了半个小时，心想是不是公式错了...

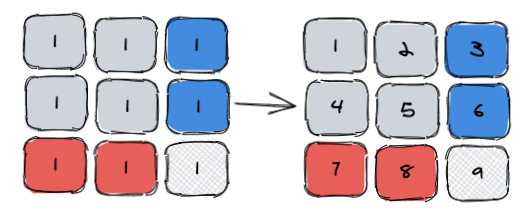
这里的图与一维数组前缀和的图不同在于，之前我们是一行行分别求前缀和，这里我本能的每增一行，都是从上一行最后一个元素的基础上加1作为起点，所以得到了这么个图，那么套入公式：

9 = 8 + 6 - 5 + 1

数学再差的同学也能立马感觉到不对，后面计算出来的数字是10，并不相等。原因其实很简单，我们在前面的图解中也解释过，8这个位置的数字不应该为8，它只应该包含前面图解中O==>C（红色区域）这6个元素，因此应该是6。

所以正确的二维数组前缀和的结果图应该是这样，这里我们直接画出来：

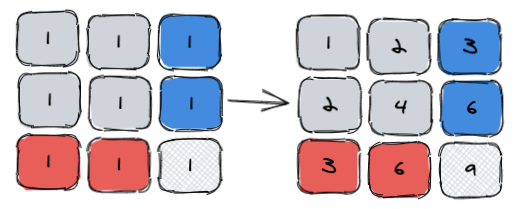
再来验证公式，非常正确：

9 = 6 + 6 - 4 + 1

那么这个二维数组前缀和的这个数字结构要怎么算出来呢？当然是套用我们前面preSum[i][j] = preSum[i][j−1] + preSum[i−1][j] − preSum[i−1][j−1] + matrix[i][j]这个公式算出来的。有同学可能就觉得不对了，以preSum(0,0)为例，它的答案很是1，但很明显我们没办法带入工时，因为不管是i-1还是j-1都超出了数组范围，怎么办？其实还是与一维数组前缀和思路相同，给每行每列都多加一维，且初始值设置为0，如下图：

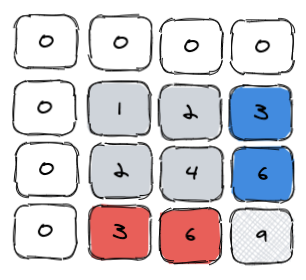
我们再来看preSum(0,0)，此时不就是0+0-0+1了么，你看这个公式是不是神了，我们要做的就是给二维数组多加一行一列，并将其都设置为0即可。

我们先来实现第一步，也就是得到一个上图这样的二维数组前缀和，我们可以先预设一个preSum的数组，它的行数应该是数组matrix行数基础加1，列数应该是matrix[i]也就是任意行的列数基础加1：

var NumMatrix = function(matrix) {
    // 先创建preSums的行
    const preSums = new Array(matrix.length+1);
    // 再为每行添加列
    for(let i =0; i < preSums.length; i++){
        // 注意，这里不能写成 preSums[i] = new Array(matrix[i].length + 1);
        // 因为很明显preSums比matrix多一行，i一定会超出matrix的范围，导致报错
        // 之所以用0，是因为矩阵中不存在每行列数不同的情况，取第一行为标准就好了
        preSums[i] = new Array(matrix[0].length + 1);
    }
    // 开始套用公式计算二维数组前缀和，同时需要初始化前缀和中第一排以及第一列为0
    for(let i = 0; i < preSums.length; i++){
        for(let j = 0; j<preSums[i].length; j++){
            // 注意，只要是定0行或者第0列，这个格子就应该是0，因此preSums就应该是0
            if (i === 0 || j === 0) {
                // 只要i是0，不管当前j是多少都应该是0，同理不管第几行，只要j是0也就是第一列，也应该是0
				preSums[i][j] = 0
			} else {
                // 否则就套用公式
				preSums[i][j] = preSums[i-1][j] + preSums[i][j-1] - preSums[i-1][j-1] + matrix[i-1][j-1]
			}
        }
    }
    // 你可以取消这行注释查看数组结构
    // console.log(preSums)
    this.preSums = preSums;
};

上面代码的注释真的是我能解释的极限了，所以就不多说啥了，那么到这里我们就套用公式得到了二维数组前缀和的结果，那么这还不够啊，因为题目是要求我们得到矩阵范围区间的和，咋整呢？

我们假设求[[1,1,1],[1,1,1],[1,1,1]]的（0,0,1,1）区间范围和，答案很清楚其实就是4，因为一共四格，问题是怎么算呢？其实还是套用二维数组前缀和公式，为了方便理解，我们还是给出图示:

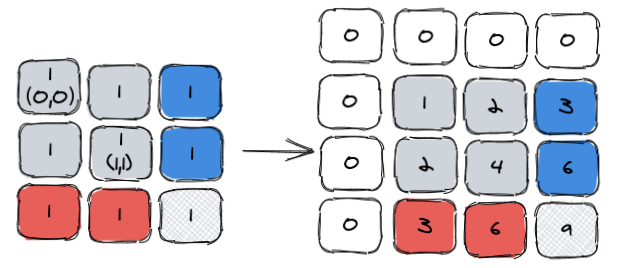
我们将最初的二维数组矩阵对应到右边的前缀和二维数组，要求的和其实还是灰色区域，如果我们还是用区域拆分的方式，你会发现灰色区域等于下图图示：

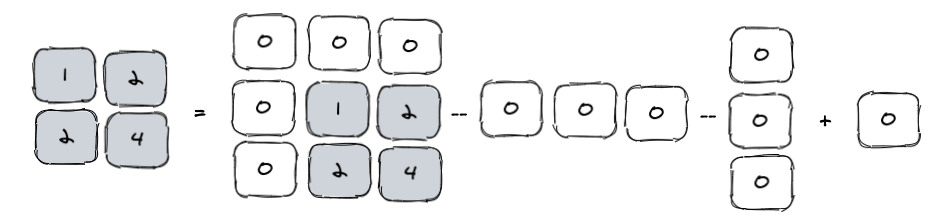
之所以最后要加一个0，也是因为前面减区域时0是交汇处，多减了一次得补回来一个，对应下来其实就是4-0-0+0。为啥横竖三个都是0，我怕大家不理解，其实横着的3个0不就是对应的就是一维数组[0,0,0]的前缀和，竖着的3个0不就是对应二维数组[[0],[0],[0]]的前缀和，所以横竖都是0。

因此满足公式：

preSums(r1,c1,r2,c2) = preSums[r2+1][c2+1] + preSums[r1][c1] - preSums[r1][c2+1] - preSums[r2+1][c1]

为了验证这一点，我们可以假设求数组[[1,1,1],[1,1,1],[1,1,1]]的（1,1,2,2）区间范围和，其实答案也是4，带入公式其实就是9+1-3-3。

如果到这里还不能理解，那建议深呼吸，洗把脸冷静下。

结合上面的代码，最终题解其实就是：

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function(matrix) {
    // 先创建preSums的行
    const preSums = new Array(matrix.length+1);
    // 再为每行添加列
    for(let i =0; i < preSums.length; i++){
        // 注意，这里不能写成 preSums[i] = new Array(matrix[i].length + 1);
        // 因为很明显preSums比matrix多一行，i一定会超出matrix的范围，导致报错
        // 之所以用0，是因为矩阵中不存在每行列数不同的情况，取第一行为标准就好了
        preSums[i] = new Array(matrix[0].length + 1);
    }
    // 开始套用公式计算二维数组前缀和，同时需要初始化前缀和中第一排以及第一列为0
    for(let i = 0; i < preSums.length; i++){
        for(let j = 0; j<preSums[i].length; j++){
            // 注意，只要是定0行或者第0列，这个格子就应该是0，因此preSums就应该是0
            if (i === 0 || j === 0) {
                // 只要i是0，不管当前j是多少都应该是0，同理不管第几行，只要j是0也就是第一列，也应该是0
				preSums[i][j] = 0
			} else {
                // 否则就套用公式
				preSums[i][j] = preSums[i-1][j] + preSums[i][j-1] - preSums[i-1][j-1] + matrix[i-1][j-1]
			}
        }
    }
    // 你可以取消这行注释查看数组结构
    // console.log(preSums)
    this.preSums = preSums;
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
    return this.preSums[row2+1][col2+1] + this.preSums[row1][col1] - this.preSums[row1][col2+1] - this.preSums[row2+1][col1]
};

你说发现长篇大论下来，围绕的还是一个二维数组求前缀和的公式展开，可能你会觉得，我要是不知道这个公式鬼做的出来，但不管怎么说，你现在知道了这个公式，就像我们以前不知道1+1=2一样，现在知道了，以后也就知道了。如果时间久了再遇到此题，我们还是可以从最简单的九宫格开始，九个格子都是1，标好ABCDO四个点，按照区域划分的思维去推导此公式。

我现在其实挺不乐意去记录这种复杂的算法题解，比如这篇文章，从理解画图到写作，前前后后用了快5个小时，LeetCode中存在上千道这样的题目，如果记录我还要用多少时间呢？可是后来一想，我不去做，不去写，可能永远都不懂这个题目的思路，不管怎么样算是把这道题啃下来了，有收获就好，哪怕一点点。

那么到这里本文结束。