DS | 折半查找二叉判定树的画法

以下给出我在学习中总结的一种比较简便的 构造折半二叉判定树 的思路以及方法：

思路分析：

在计算 \(mid\) 值时，使用的时 \(mid=(low+high)/2\) 。这里由于 \(mid\) 为 int 类型，自动默认为向下取整，因此对于一个长度为 \(n\) 序列进行划分之后的序列为 （\(0，1，2，……，mid-1\)）\(mid\)（\(mid+1，mid+2，……n-1\)），此时出现两种情况：

• 左子序列长 == 右子序列长 （ \(n=2k+1 k=0，1，2，……\)）
• 左子序列长 == 右子序列长 -1 （\(n=2k k=1，2，3，……\)）

因此可以得知，折半查找的二叉判定树 对于所有结点，左子树结点个数<=右子树结点个数。即：

1. 若某序列总长 \(n\) 为奇数，左右子树结点个数相等；
2. 若某序列总长 \(n\) 为偶数，左字数结点个数=右子树结点个数 -1 .

换句话说，对判定树中所有结点都有：

（左子树结点数-右子树结点数== -1）||（左子树结点数-右子树结点数 == 0）

由此给定某个序列，构建折半查找判定树方法如下三步：

1. 按照结点总数先画出最大的满二叉树结构，并计算剩余几个结点。
2. 将剩余结点按照上述的规律依次填入最底层即为二叉判定树的树形。
3. 将给定序列依次按照 中序遍历 顺序填入各个结点。

---

具体如下面的例子：

例：画出（\(2，5，7，10，14，15，18，23，35，41，52\)）的折半查找判定树。

序列总长度为 \(n=11>2^3-1\) 即二叉判定树为 \(4\) 层，前三层为满二叉树结构，剩余 \(4\) 个结点。

先画出 前三层 结构。

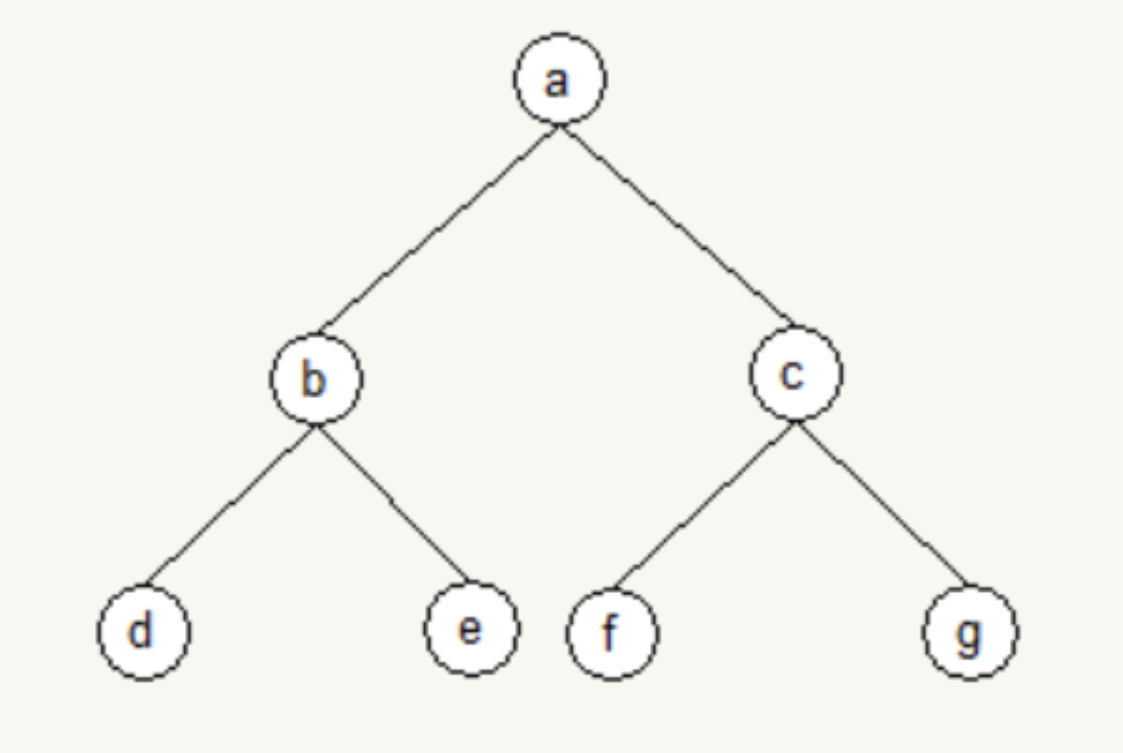
1）插入第一个结点 \(h\)。

\(a\) 的左右子树结点个数相等，所以新的结点应加入 \(a\) 的右子树；再看 \(a\) 的右子树，\(c\) 的左右子树结点个数相等，所以新结点应加入 \(c\) 的右子树；再看 \(c\) 的右子树，\(g\) 的左右子树结点个数相等，所以新结点应加入 \(g\) 的右子树；如图

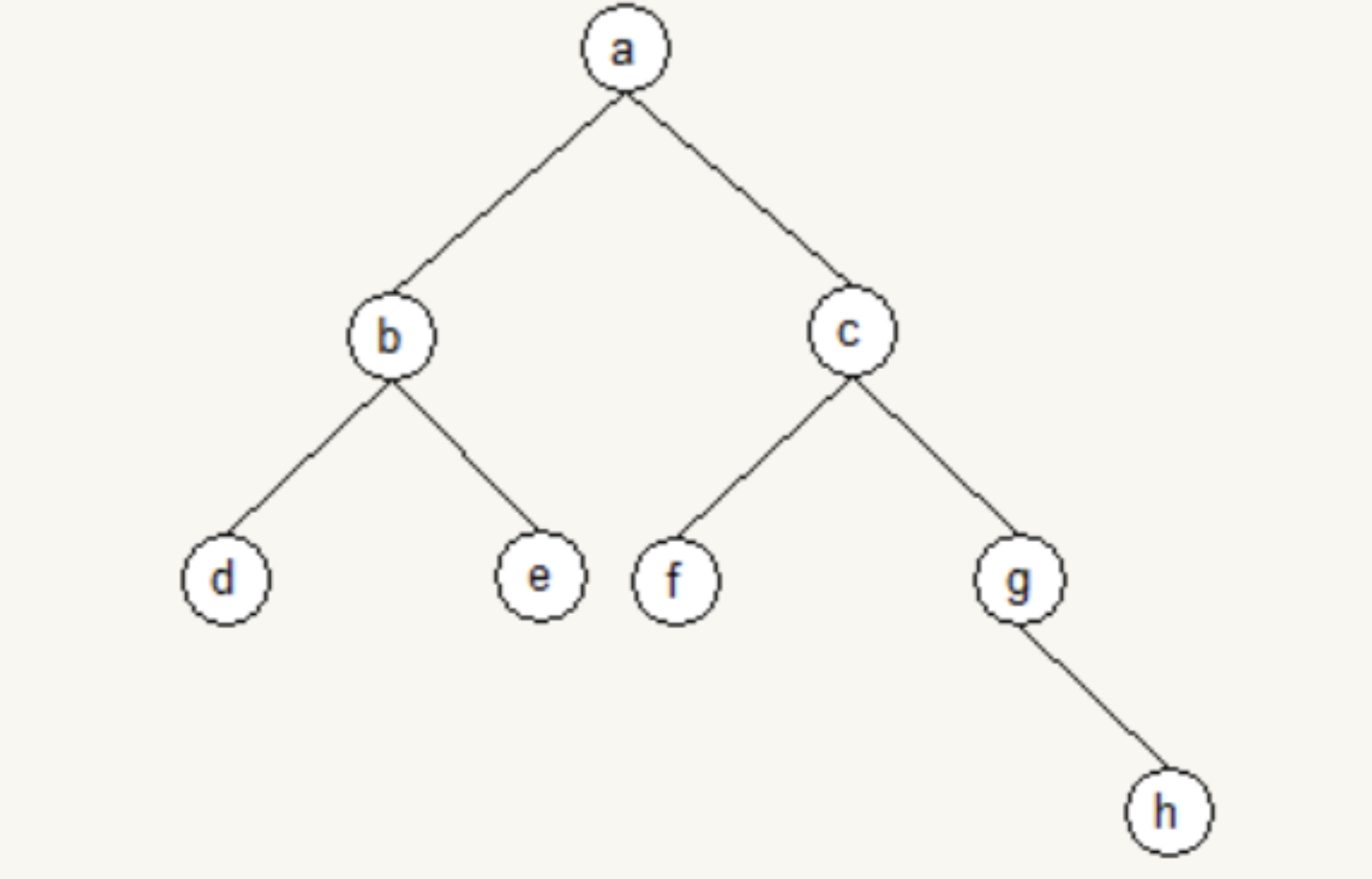
2）第二个结点 \(i\)。\(a\) 的 左子树结点数 - 右子树结点数 = -1，所以新结点应加入 \(a\) 的左子树（若加入右子树，对于 \(a\) 来说左右子树结点之差 = \(-2\) ，不符合规律）；再看 \(a\) 的左子树，\(b\) 的左右子树结点个数相等，所以新结点应加入 \(b\) 的右子树；再看 \(b\) 的右子树，\(e\) 的左右子树结点个数相等，所以新结点应加入 \(e\) 的右子树。如图

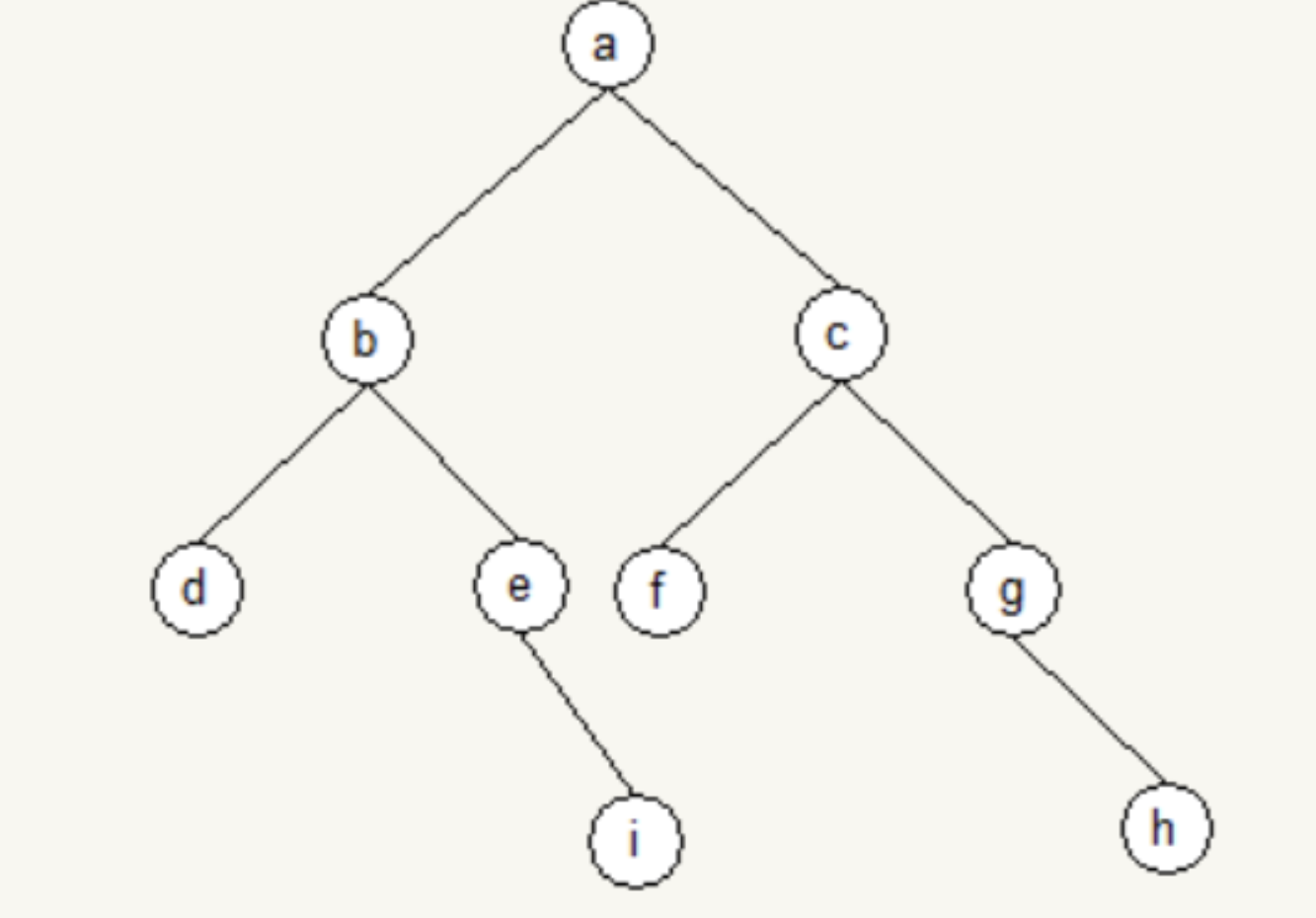
3）同理分析，第三个结点应加在如图位置。

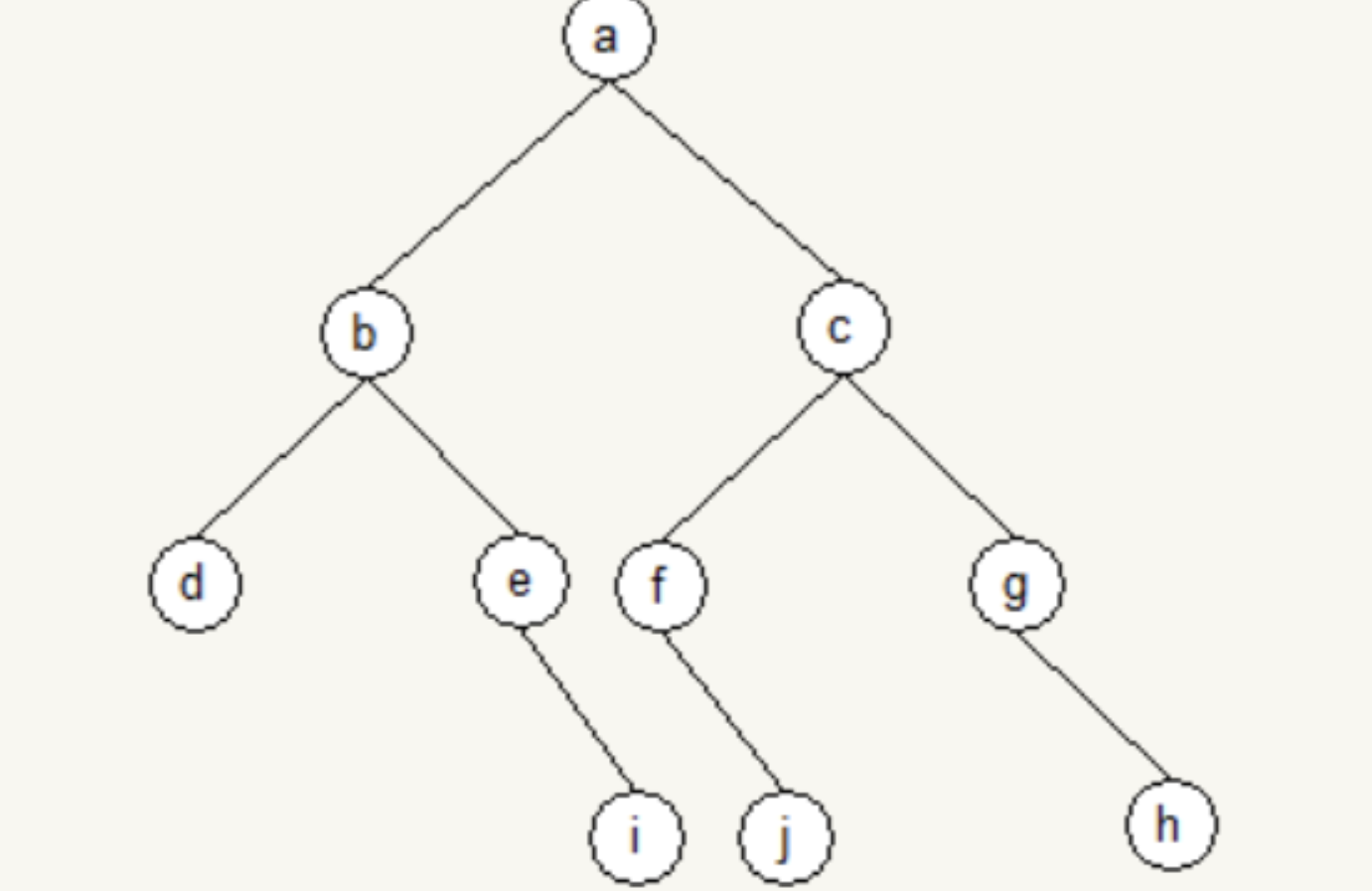
4）第四个结点加在如图位置。

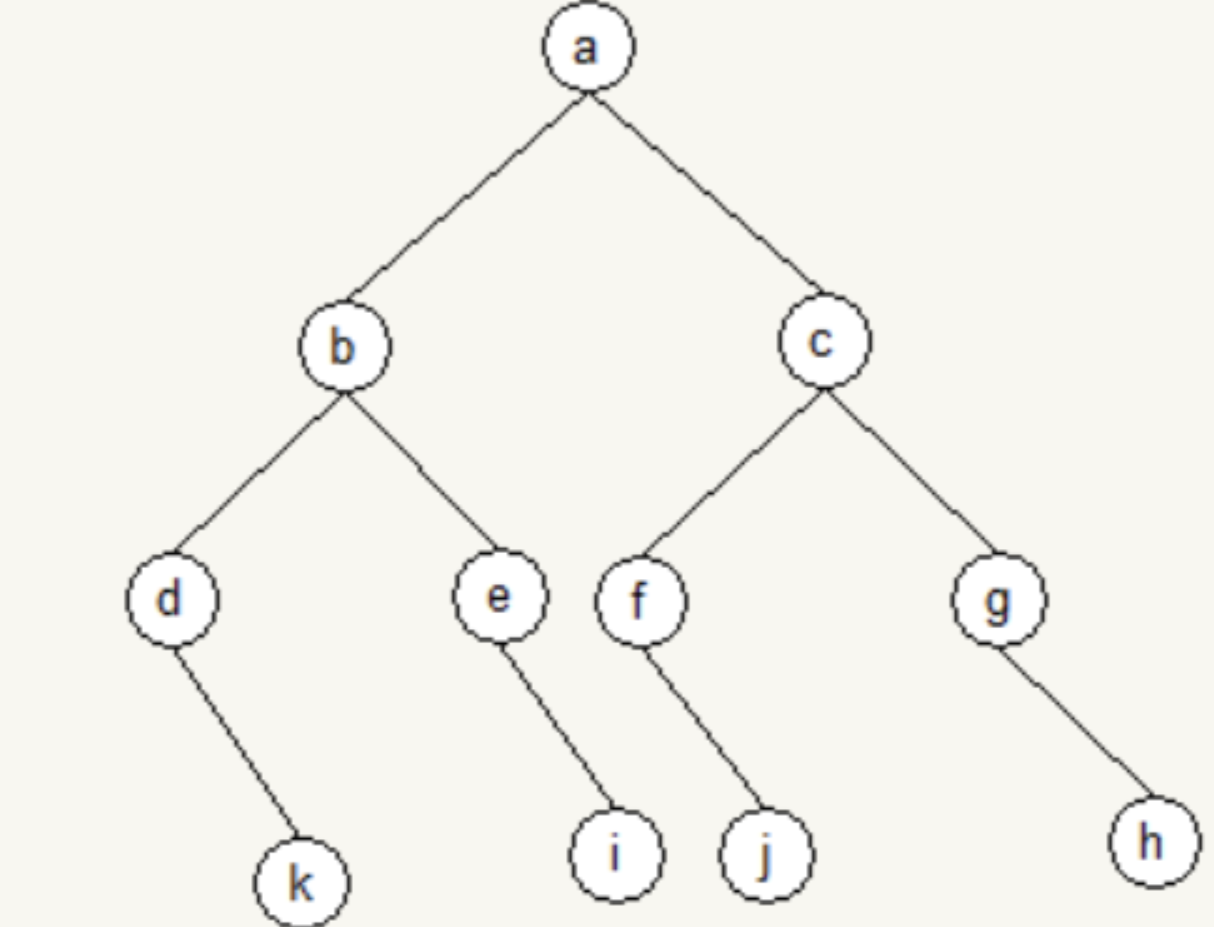
得到最终的树形如上图。（字母编号不唯一，后面中序遍历结果会不同）

该二叉树的中序遍历顺序为 \(dkbeiafjcgh\) ，

分别对应 \(2，5，7，10，14，15，18，23，35，41，52\) 。因此将序列一一对应填入树中，即

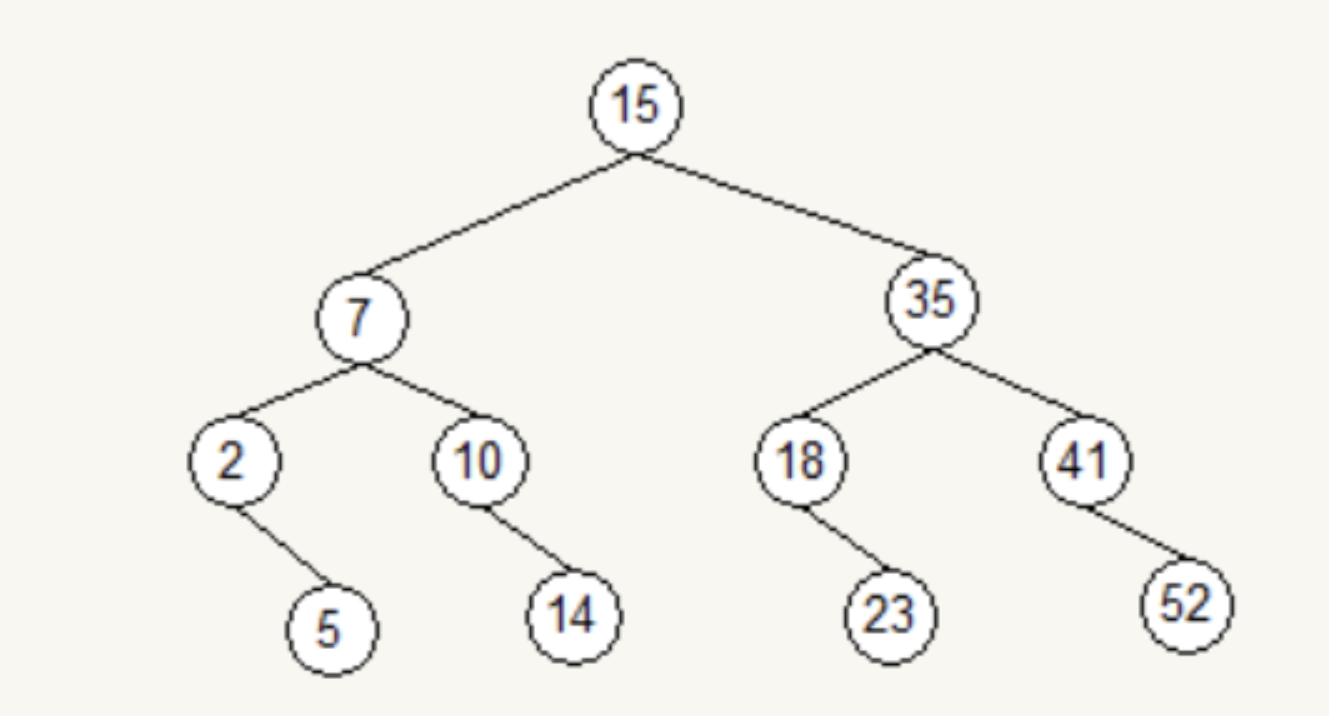
该树即为此序列的二叉判定树。

做题过程中熟练使用此方法比通过算法模拟来推断二叉判定树的速度要快许多倍。

在平时做题过程中，涉及到需要具体画出二叉判定树的题目，往往结点个数（序列长度）不超过\(2^4-1=15\) 个，即一般为高度不超过4的树，因此可以在练习时将结点个数 \(8-14\) 的所有树形画几遍，就可以很熟练的掌握这个方法。

二叉判定树画出之后便可以对其他具体题目进行分别的计算，如求成功或失败的查找长度、求比较顺序、比较次数等。