Tarjan 算法——图论学习笔记

Part.1 引入

在图论问题中，我们经常去研究一些连通性问题，比如：

• 有向图的联通性：传递闭包——Floyd 算法；
• 有向图连通性的对称性：强联通分量（SCC）——Tarjan 算法缩点；
• 无向图的联通性：并查集；
• 无向图的关键边：桥（割边）、边双——Tarjan 算法缩点；
• 无向图的关键点：割点、点双——Tarjan 建立圆方树。

那么，Tarjan 算法到底是什么呢？

Part.2 Tarjan 算法求 SCC

SCC，即强联通分量，是一张有向图的极大子图，满足任意两个点 \(u,v\) 强联通（即 \(u\) 可以到 \(v\)，\(v\) 可以到 \(u\)）。一个重要的性质就是强联通具有传递性。

在有向图中，我们会用 Tarjan 算法去建一棵 DFS 生成树：

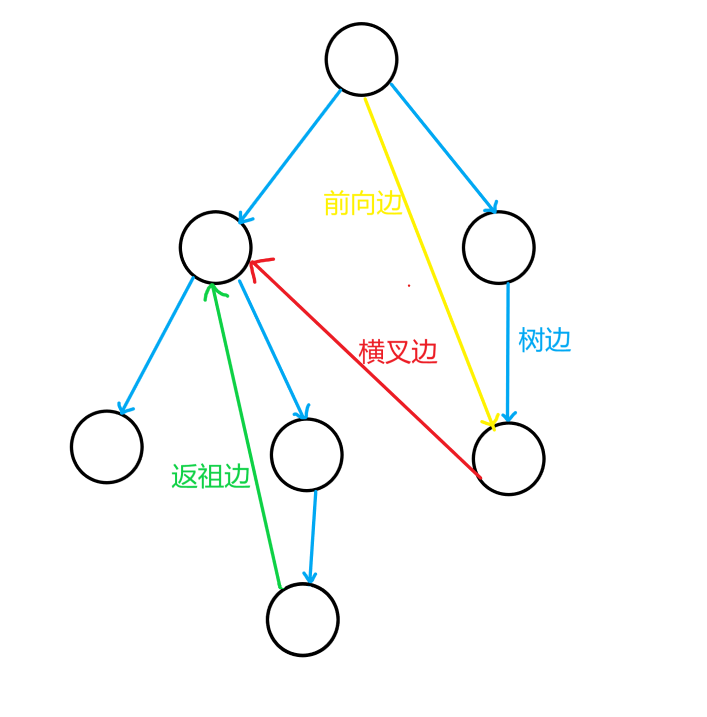
在 DFS 的过程中，我们会对于每个点，处理出一个 DFS 序号，并把 DFS 到的点放入一个栈中，定义一个新数组 \(low\)，其中，\(low_x\) 表示 \(x\) 号节点能跳到的在栈中的 DFS 序的最小值。

接下来就是 Tarjan 算法的核心思想：对于一个点 \(u\)，如果满足 \(dfn_u=low_u\)，说明点 \(u\) 不存在向上跳的非树边，是一个顶点。那么当前节点及以后在栈中的节点就构成了一个 SCC。

代码如下：

int dfn[N],low[N],idx,stk[N],top,scc[N],c;
bool inc[N];
void dfs(int u)
{
	dfn[u] = low[u] = ++idx,stk[++top] = u,inc[u] = 1;
	for(int i = head[u];i;i = nxt[i])//建 DFS 树且维护 low 数组
	{
		int v = to[i];
		if(!dfn[v])//树边
		{
			dfs(v);
			low[u] = min(low[u],low[v]);
		}
		else if(inc[v]) low[u] = min(low[u],dfn[v]);//非树边
	}
	if(dfn[u]==low[u])//是一个顶点，构成一个 SCC
	{
		c++;//SCC个数+1
		while(stk[top]!=u)
			inc[stk[top]] = 0,scc[stk[top]] = c,top--;
		inc[u] = 0,scc[u] = c,top--;
	}
}

求 SCC 有什么用呢？

• 在一些与连通性有关的问题中，我们把每个 SCC 缩成一个点，可以得到一个 DAG，因为如果还环的话就能形成一个新的 SCC。这样就可以在 DAG 上做 DP 之类来解决问题；
• 在 2-SAT 问题（有 \(m\) 个二元方程，并且每个未知数都是 \(0\) 或 \(1\)）中，我们求解和判无解也需要用到 SCC，有兴趣的可以自己去看。

Part.3 Tarjan 求割边、边双

在无向图中，定义割边（也叫桥）为删掉这条边后图的连通性改变的边。边双连通分量（简称边双），即为不存在割边的极大子图，与 SCC 一样，具有传递性。

和求 SCC 一样，我们还是去建立一颗 DFS 树。我们重新定义 \(low_x\) 为 \(x\) 号节点最多通过一条非树边能跳到的 DFS 序的最小值。那一条连接 \(u,v\) 的边是桥当且仅当 \(dfn_u<low_v\)，就相当于 \(v\) 经过一条非树边到不了 \(u\)，这样肯定是割边。

至于求边双，就是每次选一个点，在不经过桥的前提下能到的所有点就形成了一个边双。

一个细节就是边表的 cnt 记得赋值为 \(1\)，方便求反向边。

代码和求 SCC 差不多，具体如下：

int n,m,dfn[N],low[N],t;
bool brg[M];
void dfs(int u,int ine)//求割边
{
	dfn[u] = low[u] = ++t;
	for(int i = head[u];i;i = nxt[i])
	{
		if(i==ine) continue;//不往回走
		int v = to[i];
		if(dfn[v]==0)
		{
			dfs(v,i^1);
			low[u] = min(low[u],low[v]);
			if(low[v]>dfn[u]) brg[i] = brg[i^1] = 1;//是割边
		}
		else low[u] = min(low[u],dfn[v]);
	}
}
bool vis[N];
int c;//记录边双的个数
void dfs(int u)
{
	ans[c].push_back(u),vis[u] = 1;
	for(int i = head[u];i;i = nxt[i])
	{
		if(brg[i]) continue;//不经过桥
		int v = to[i];
		if(!vis[v]) dfs(v);
	}
}

Part.4 Tarjan 求割点、点双

参照割边、边双的定义，割点为删掉这个点后图的连通性改变的点。点双连通分量（简称点双），即为不存在割点的极大子图。但是点双不具有传递性，所以点双是最难的。画一个图就知道了：

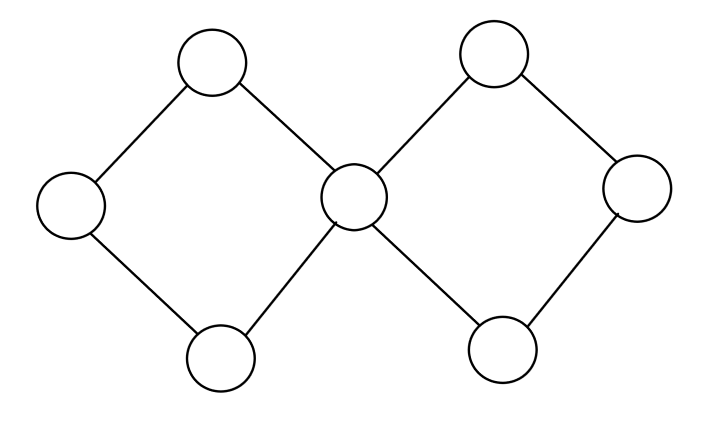
左边 \(4\) 个点是个点双，右边 \(4\) 个点也是点双，但是整张图却不是点双，因为中间的点是个割点。

仍然建出 DFS 树，发现用顶点找出一个点双已经不可行了，因为一个点能在多个点双当中。

我们发现，两个点双至多有一个交点，这个点就是割点。如上图，这个交点一定在下面的点双中 \(dfn\) 是最小的，而上面的点双可以由另外的点（类似树根）求出。

所以，对于一条边 \((u,v)\)，如果满足 \(low_v\ge dfn_u\)，就说明找到一个点双了。

上代码：

int n,m,dfn[N],low[N],c,stk[N],top,t;
vector<int> ans[N];
void dfs(int u,int fa)
{
	dfn[u] = low[u] = ++t;
	stk[++top] = u;
	int son = 0;
	for(int i = head[u];i;i = nxt[i])
	{
		int v = to[i];
		if(v==fa) continue;
		if(dfn[v]==0)
		{
			++son;
			dfs(v,u);
			low[u] = min(low[u],low[v]);
			if(low[v]>=dfn[u])//找到点双
			{
				++c;
				while(stk[top]!=v) ans[c].push_back(stk[top--]);
				ans[c].push_back(v);--top;ans[c].push_back(u);//细节：不能将点 u 弹出栈
			}
		}
		else low[u] = min(low[u],dfn[v]);
	}
	if(fa==0&&son==0) ans[++c].push_back(u);//特判：单独一个点也是点双
}

点双有一个巨大的应用——圆方树。

圆方树，就是对于每个点双，新建一个方点，断掉点双原图中的边，然后点双里所有的点向这个方点连边。这样形成的结构就是一棵树。举个例子：

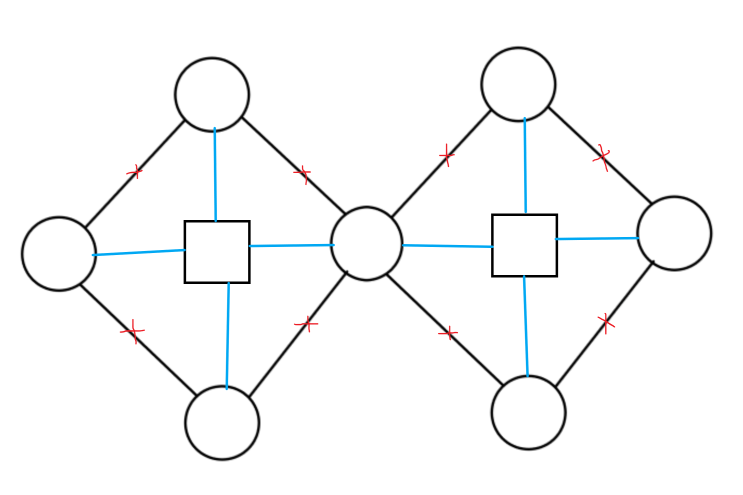
这样，图上问题就变成了树上问题，是不是简单很多？

那圆方树还有什么应用呢？

• 求 可行路径/必经点 的一些东西。可行路径就对应圆方树上两点的路径加上与树上路径的方点直接相连的点，必经点就是树上路径的圆点；

• 仙人掌图：比如 P5236，通过重新定义边权，将仙人掌上最短路变为树上路径。

顺便提一句，图上问题就变成了树上问题大多都要判断两点 LCA 为方点的情况。

Part.5 总结

Tarjan 算法在图论问题中有大用，特别是有关联通性的题。

写字不易，给个赞吧~

\[\text {THE END}
\]