机器学习|K邻近(K Nearest-Neighbours)

本文从概念、原理、距离函数、K 值选择、K 值影响、、优缺点、应用几方面详细讲述了 KNN 算法

K 近临(K Nearest-Neighbours)

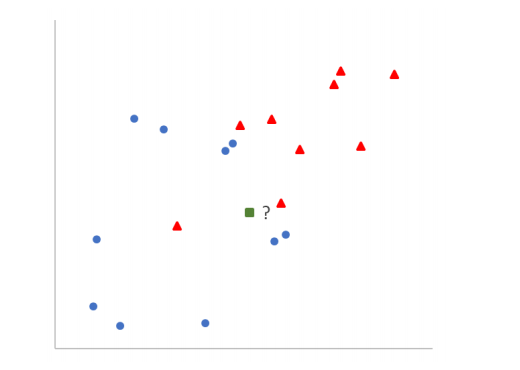
一种简单的监督学习算法，惰性学习算法，在技术上并不训练模型来预测。适用于分类和回归任务。它的核心思想是：相似的对象彼此接近。例如，若果你想分类一个新的数据点(绿点)，可以查看训练数据中哪些数据点与它最接近，并根据这些最接近的数据点和标签来预测它的标签(红点或蓝圆)。

概念

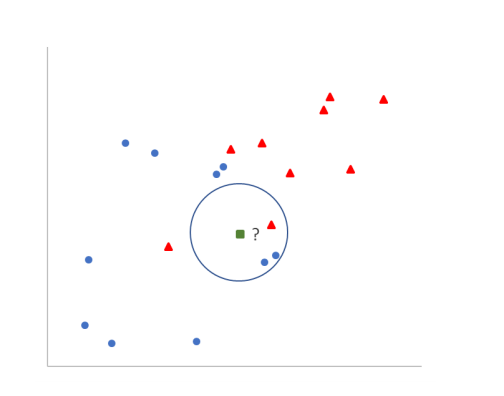
K: 这是一个用户指定的正整数，即训练数据分类数量，代表要考虑的最近邻居的数量，上图中假设 K=2,即训练数据分类为蓝色圆和红色三角两类标签。

距离函数: 用于计算数据点之间的距离。最常见的是欧几里得距离、曼哈顿距离、马氏距离等。

投票机制:

分类任务: 将根据 k 个最近邻的多数投票来确定新数据点的类别。
回归任务: 通常取 k 个最近邻的输出变量的平均值。

原理

距离计算： 对于给定的新数据点，计算它与训练数据集中每个点的距离。
选取 K 个邻居： 从训练数据集中选取距离最近的 K 个点。
投票 (对于分类)： 对于 K 个邻居，看哪个类别最为常见，并将其指定为新数据点的类别。
均值 (对于回归)： 对于 K 个邻居，计算其属性的平均值，并将其指定为新数据点的值。

距离度量

欧几里得距离 (Euclidean Distance)

欧几里得距离的名称来源于古希腊数学家欧几里得，是衡量两点在平面或更高维空间中的"直线"距离。它基于勾股定理，用于计算两点之间的最短距离。在日常生活中，我们经常无意识地使用欧几里得距离，例如，当我们说两地之间的"直线"距离时，实际上是在引用欧几里得距离。

公式:

给定两点 P 和 Q，其坐标分别为 $P(x_1, x_2, ..., x_n)$ 和 $Q(y_1, y_2, ..., y_n)$ 在一个 n 维空间中，它们之间的欧几里得距离 d 定义为：

$d(P, Q) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}$

曼哈顿距离 (Manhattan Distance)

曼哈顿距离得名于纽约的曼哈顿，因为在曼哈顿的街道布局是网格状的。想象一下，你在一个街区的一个角落，要走到对面的角落，你不能直接穿越街区，只能沿着街道走。这就是曼哈顿距离的来源，也因此它有时被称为“城市街区距离”。

公式

给定两点 P 和 Q，其坐标分别为 $P(x_1, x_2, ..., x_n)$ 和 $Q(y_1, y_2, ..., y_n)$ 在一个 n 维空间中，它们之间的曼哈顿距离 L1 定义为：

$L1(P, Q) = \sum_{i=1}^{n} |x_i - y_i|$

闵可夫斯基距离 (Minkowski Distance)

闵可夫斯基距离是一种在向量空间中度量两个点之间距离的方法。它实际上是一种泛化的距离度量，可以看作是其他距离度量（如欧几里得距离、曼哈顿距离）的泛化。通过改变一个参数p，它可以表示多种距离度量。

公式

给定两点 P 和 Q，其坐标分别为 $P(x_1, x_2, ..., x_n)$ 和 $Q(y_1, y_2, ..., y_n)$ 在一个 n 维空间中，它们之间的闵可夫斯基距离 Lp 定义为：

$Lp(P, Q) = \left( \sum_{i=1}^{n} |x_i - y_i|^p \right)^{\frac{1}{p}}$

其中 p 是一个大于等于 1 的实数。特定的 p 值会导致其他常见的距离度量：

当 p = 1 时，这变成了曼哈顿距离。
当 p = 2 时，这变成了欧几里得距离。

余弦相似性 (Cosine Similarity)

余弦相似性度量了两个向量方向的相似度，而不是它们的大小。换句话说，它是通过比较两个向量之间的夹角来测量它们的相似性的。夹角越小，相似性就越高。

它经常在高维空间中（如 TF-IDF 权重的文档向量）使用，因为在高维空间中，基于欧几里得距离的相似性度量可能不太有效。

公式

给定两个向量 A 和 B，它们的余弦相似性定义为：

$\text{cosine similarity}(A, B) = \frac{A \cdot B}{\|A\| \|B\|}$

其中：

$A \cdot B$ 是向量 A 和 B 的点积。
$\|A\|$ 和 $\|B\|$ 分别是向量 A 和 B 的欧几里得长度（或模）。

公式可以进一步扩展为：

$\text{cosine similarity}(A, B) = \frac{\sum_{i=1}^{n} A_i B_i}{\sqrt{\sum_{i=1}^{n} A_i^2} \sqrt{\sum_{i=1}^{n} B_i^2}}$

这里，n 是向量的维度，而 $A_i$ 和 $B_i$ 分别是向量 A 和 B 在第 i 维度上的值。

余弦相似性值范围为[-1, 1]，其中 1 表示完全相似，0 表示不相关，而-1 表示完全相异。

K 值的确定方法：

交叉验证： 这是确定 k 值的最常用方法。对于每一个可能的 k 值，使用交叉验证计算模型的预测错误率，选择错误率最低的 k 值。
启发式方法： 有时，可以选择 sqrt(n)作为起始点，其中 n 是训练样本的数量。这只是一个粗略的估计，通常需要进一步验证。
误差曲线： 画出不同 k 值对应的误差率曲线，选择误差变化开始平稳的点。
领域知识： 在某些应用中，基于领域知识和经验选择 k 值可能更为合适。

K 值的影响：

过小的 k 值：

分类：模型可能变得过于敏感和复杂。它可能对训练数据中的噪声或异常点特别敏感，从而容易过拟合。当 k=1 时，任何训练数据中的异常点都可能影响预测结果。
回归：模型可能会受到异常值的强烈影响，导致预测结果出现明显的波动。

过大的 k 值：

分类：模型可能变得过于简化。随着 k 值的增加，分类决策的边界会变得更加平滑，可能会忽视数据中的细微模式，导致欠拟合。
回归：模型同样可能会过于简化。大 k 值使模型的预测偏向于所有数据点的平均值，因此可能会忽视数据中的局部特性或细节。

优缺点

优点

简单且直观。

无需训练阶段，适用于动态变化的数据集。

对异常值不敏感（取决于 K 的大小）。

缺点

计算复杂度高，因为对于每一个新的数据点，都需要与所有训练数据计算距离。

需要决定 K 的大小，这可能会影响结果。

高维数据中的性能下降。

应用场景：

推荐系统:
- 基于用户之前的喜好推荐相似电影
- 推荐用户可能喜欢的曲目或歌手
文本分类:

区分垃圾邮件和正常邮件。
图像识别: 识别包括上的手写邮政编码，分类投递邮件包裹
医疗诊断： 预测患者可能的疾病风险。
信用评分：预测客户的信用风险。
欺诈检测：识别信用卡中的异常交易。
位置基服务：基于位置提供餐厅或服务推荐。