一次考试的T3

啊这
感觉不太可做
观察性质，发现这个字符串只由ABC构成
这个性质必须利用
仅仅由3种字符组成意味着什么呢?
这个字符串只有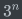种可能性
这个有什么用呢？
只是说明暴力枚举的时间复杂度会小一些而已。
不止是这些。

首先有一些的性质

1.如果这个栈的顶端和当前的字符是一样的，那么肯定是直接取出来的
2.如果这个栈的第二的字符和当前的字符是一样的，那么先弹出一个然后输出肯定是不会不优
3.必定存在一个转折点，这个转折点前的决策方法如上，这个转折点后的决策方法是一直弹出知道这个字符被找到然后在输出,因为栈中的字符一定是3个字符在循环，所以每次最多就只会有400个字符
我们枚举这个转折点， 然后在暴力按照上面的方法进行模拟，是的

这个比普通的暴力优秀的原因就是因为他枚举了一个关键——转折点
这个其实才是最重要的性质

这个我会给出证明。

考虑一个序列S​，对于一个没有转折点的模拟方法，那么在最后可能会在栈中留下很多的字符，这些肯定是要最后弹出的，我们就先忽略掉弹出的花费，因为在这两种情况中，最后弹出的花费是一样的。

在最后，如果在这个栈里面有很多的数，我们在后面加数的话，就必定是要1到3的花费，而如果我们只是弹出的话，只需要1即可。说明在可以的情况下，弹出数字来寻找数字，是要比加入更优秀的。

那么，为什么不可以弹出寻找后在继续加入，然后在弹出呢？(即是有多个转折点)
在中间的时候如果要弹出来寻找的话，那么就是如上面所说的情况1,和2，肯定是这两种决策更优的。

所以，肯定有且仅有一个转折点。

然后直接按照这种进行枚举就行了

code

//加油
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
char c[1001];
int n,m,ans=INT_MAX,len,a[10001],q[100001];
void work(int mid)
{
    int sum=0,top=0;
    for(int j=1;j<=mid;j++)
    {
        if(top>=1&&a[j]==q[top])sum++;
        else
        if(top>=2&&a[j]==q[top-1])top--,sum+=2;
        else
        q[++top]=a[j],sum+=2;
    }
    for(int j=mid+1;j<=len;j++)
    {
        while(top&&q[top]!=a[j])sum++,top--;
        if(top==0)sum+=2;
        sum++;
    }
    ans=min(ans,sum+top);
}
int main()
{
    freopen("letter.in","r",stdin);
    freopen("letter.out","w",stdout);
    string s;
    cin>>s;
    for(int i=0;i<s.size();i++)
    a[i+1]=s[i]-'A'+1;
    len=s.size();
    for(int i=1;i<=len;i++)
    {
        work(i);
    }
    cout<<ans<<endl;
    return 0;
}

至于怎么想到这中做法的，其实还是性质的分析，如果能够想到这种转折点的证明，那么就应该只能够比较顺理成章的想到这种方法。
转折点其实就是关于贡献的一种性质，在思考利用最后的栈中的数的时候应该能够想到。

这种题目我是第一次遇到，栈和字符串的结合。主要还是思考决策的方法，然后对其进行一定的利用。
但是存在特殊的情况的题目比较的常见，想这种字符串只由ABC组成的。还有上次我遇到的线段树的题目，a[i]<1000，操作是求区间的所有的子区间的异或和的和，存在异或这种与只与二进制有关的操作。
都是对于题目特殊性质的应用。

这种就是要去思考这种特殊的性质要什么效果和使用方法就可以想到正解了