关于"覆盖问题”的反思

[HAOI2007]覆盖问题

题目描述

某人在山上种了N棵小树苗。冬天来了，温度急速下降，小树苗脆弱得不堪一击，于是树主人想用一些塑料薄膜把这些小树遮盖起来，经过一番长久的思考，他决定 用3个L*L的正方形塑料薄膜将小树遮起来。我们不妨将山建立一个平面直角坐标系，设第i棵小树的坐标为（Xi,Yi），3个L*L的正方形的边要求平行 与坐标轴，一个点如果在正方形的边界上，也算作被覆盖。当然，我们希望塑料薄膜面积越小越好，即求L最小值。

输入格式

第一行有一个正整数N，表示有多少棵树。

接下来有N行，第i+1行有2个整数Xi,Yi，表示第i棵树的坐标，保证不会有2个树的坐标相同。

输出格式

一行，输出最小的L值。

样例 #1

样例输入 #1

4
0 1
0 -1
1 0
-1 0

样例输出 #1

1

提示

数据范围

100%的数据，-1,000,000,000<=Xi,Yi<=1,000,000,000

30%的数据，N<=100

50%的数据，N<=2000

100%的数据，N<=20000

---

---

我一直困扰自己的错误思路：

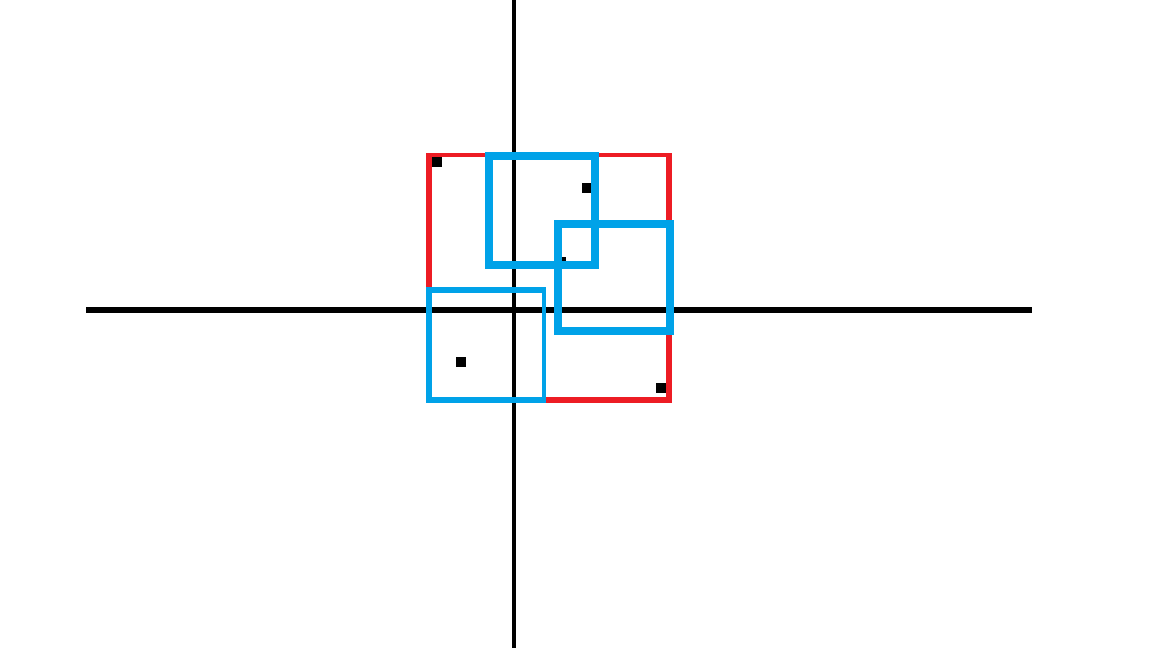
一定会有一个点在角上，另外两个点紧挨边

实际上的正确想法是，



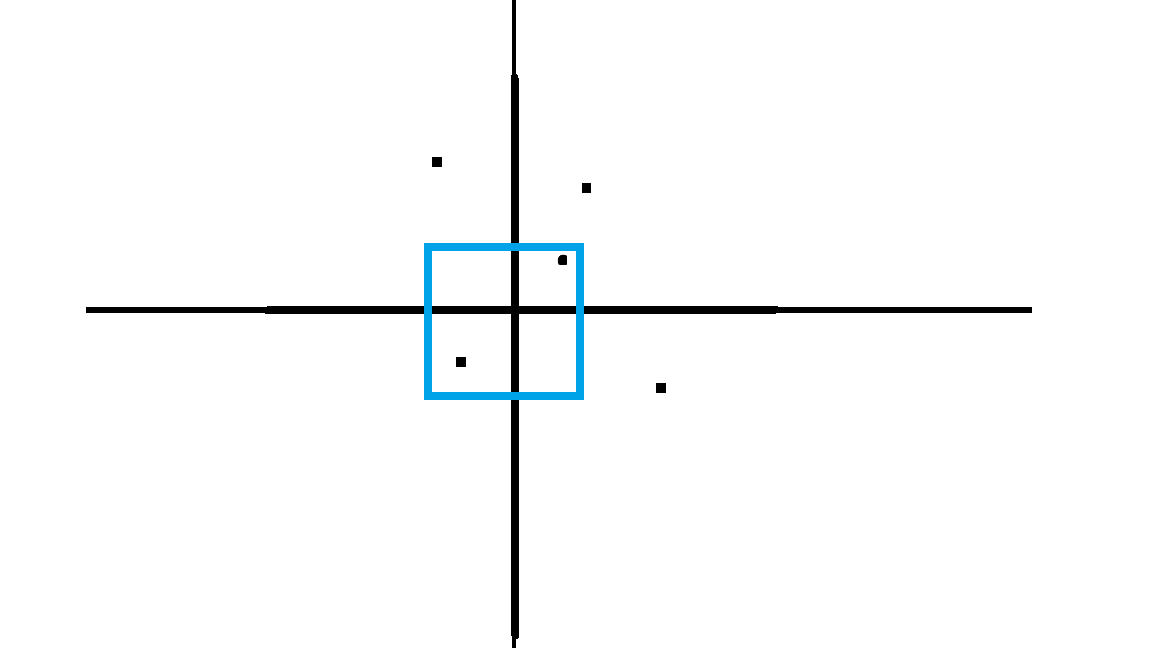
在铺好一块塑料布之后，删去已经铺好的点，剩下的点仍然是无序的，也就是第二三块与第一块的情况是相同的。

判断的式子也是相同的，不存在紧挨着边之类的问题。

另外，范围只有$ 20000 $，可以尝试一些复杂度较高的暴力。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int x[20010],y[20010];
int n;
int v[20010];
bool check(int l,int c)
{
	int xi=INT_MAX,xa=INT_MIN,yi=INT_MAX,ya=INT_MIN;
	for(int i=1;i<=n;i++)
		if(!v[i])
		{
			xi=min(xi,x[i]);
			xa=max(xa,x[i]);
			yi=min(yi,y[i]);
			ya=max(ya,y[i]);
		}
	bool ll=1;
	for(int i=1;i<=n;i++)
		if(!v[i])
		{
			if(x[i]>=xi&&x[i]<=xi+l&&y[i]>=yi&&y[i]<=yi+l)
				v[i]=c;
			else
			{
				ll=0;
			}
		}
	if(c!=3) ll=check(l,c+1);
	for(int i=1;i<=n;i++)
		if(v[i]==c)
			v[i]=0;
	if(ll) return 1;
	ll=1;
	for(int i=1;i<=n;i++)
		if(!v[i])
			if(x[i]>=xi&&x[i]<=xi+l&&y[i]>=ya-l&&y[i]<=ya)
				v[i]=c;
			else
				ll=0;
	if(c!=3) ll=check(l,c+1);
	for(int i=1;i<=n;i++)
		if(v[i]==c)
			v[i]=0;
	if(ll) return 1;
	ll=1;
	for(int i=1;i<=n;i++)
		if(!v[i])
			if(x[i]>=xa-l&&x[i]<=xa&&y[i]>=yi&&y[i]<=yi+l)
				v[i]=c;
			else
				ll=0;
	if(c!=3) ll=check(l,c+1);
	for(int i=1;i<=n;i++)
		if(v[i]==c)
			v[i]=0;
	if(ll) return 1;
	ll=1;
	for(int i=1;i<=n;i++)
		if(!v[i])
		{
			if(x[i]>=xa-l&&x[i]<=xa&&y[i]>=ya-l&&y[i]<=ya)
				v[i]=c;
			else
			{
				ll=0;
			}
		}
	if(c!=3) ll=check(l,c+1);
	for(int i=1;i<=n;i++)
		if(v[i]==c)
			v[i]=0;
	if(ll) return 1;
	for(int i=1;i<=n;i++)
		if(v[i]==c)
			v[i]=0;
	return 0;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d%d",&x[i],&y[i]);
	memset(v,0,sizeof(v));
	int l=1,r=INT_MAX-3;
	while(l<r)
	{
		memset(v,0,sizeof(v));
		int mid=(l+r)/2;
		if(check(mid,1)) r=mid;
		else l=mid+1;
	}
	printf("%d",l);
	return 0;
}
/*
5
2 2
3 5
6 -3
-2 -2
-3 6
*/