[HAOI2018] 字串覆盖

[HAOI2018]字串覆盖

题目描述

小C对字符串颇有研究，他觉得传统的字符串匹配太无聊了，于是他想到了这

样一个问题．

对于两个长度为n的串A, B, 小C每次会给出给出4个参数s, t, l, r. 令A从s到t的

子串(从1开始标号)为T，令B从l到r的子串为P.然后他会进行下面的操作：

如果T的某个子串与P相同，我们就可以删掉T的这个子串，并获得K − i的收

益，其中i是初始时A中(注意不是T中)这个子串的起始位置，K是给定的参数．

删除操作可以进行任意多次，你需要输出获得收益的最大值．

注意每次询问都是独立的，即进行一次询问后，删掉的位置会复原．

输入格式

从文件cover.in中读入数据.

第一行两个整数n, K，表示字符串长度和参数．

接下来一行一个字符串A.

接下来一行一个字符串B.

接下来一行一个整数q，表示询问个数．

接下来q行，每行四个整数s, t, l, r，表示一次询问．

输出格式

输出到文件cover.out中.

输出q行，每行一个整数，表示一个询问的答案．

样例 #1

样例输入 #1

10 11
abcbababab
ababcbabab
5
1 9 7 9
3 10 8 10
1 10 1 2
5 7 2 3
1 5 3 6

样例输出 #1

6
10
22
5
10

提示

样例1解释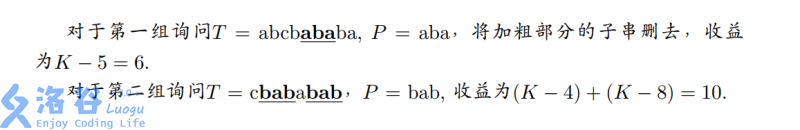

子任务

对于所有数据，有 $ 1 ≤ n, q ≤ 10^5 $ ，A, B仅由小写英文字母组成，$ 1 ≤ s ≤ t ≤n $ , $ 1 ≤ l ≤ r ≤ n $ , $ n < K ≤ 10^9 $ ．

HAOI2018 round1 T3

对于 $ n = 10^5 $ 的测试点，满足\(51≤r−l≤2*10^3\) 的询问不超过11000个，且r−l在该区间内均匀随机

作为一道省选压轴题，这题还是偏简单的。

有一个很显然的贪心：一定是尽量地往前选，选越多越好。因为 \(k>n\)，同时选的 \(k-i\) 中 \(i\) 一定是越小越好。

见到这个数据范围，明显要求我们分类分成 \(r-l>50\) 和 \(r-l\le 50\) 来处理

\(r-l>50\) 的方法就非常板子了。容易发现当 \(r-l>2000\) 的时候，选的串的个数一定不超过 $|S|\div(r-l)\le50 $，这就变成了一个字符串题。对S 建 SAM 后，找到 T[l...r] 所对应的等价类。怎么找等价类呢？可以建SAM 时把两个串连在一起建，然后在两个串中间放一些特殊字符，然后只要找到 \(T\) 对应的等价类就可以了。可以在 SAM 上用线段树合并维护等价类出现位置，然后每次线段树二分出下一个选的地方在哪就行了。而在 \(51\le r-l\le 2000\) 时，串的个数不超过 \(|S|\div r-l\le 2000\)，同时询问还只有 \(11000\) 次，带个 log 3s 还是跑的过去的。

当 \(r-l\le 50\) 的时候，考虑把所有串给找出来跑。枚举所有长度不超过 50 的串，然后把那些一样的给找出来。对于每个询问，可以用倍增去统计就行了。

#include<bits/stdc++.h>
#define vit vector<int>::iterator
using namespace std;
typedef long long LL;
const int N=1e5+5,INF=2e9;
int k,n,TME,tme,nx[N][20];
LL ans[N],ns[N][20];
char s[N],t[N];
vector<int>p[51],q[N<<2],g[N];
string str;
map<string,int>mp;
struct query{
    int l,r,s,t,id;
}qu[N];
template<int N>struct segment{
    int tr[N],lc[N],rc[N],idx;
    void update(int&o,int l,int r,int x)
    {
        if(!o)
            o=++idx;
        if(l==r)
            return;
        int md=l+r>>1;
        if(md>=x)
            update(lc[o],l,md,x);
        else
            update(rc[o],md+1,r,x);
    }
    int merge(int p,int q)
    {
        if(!p||!q)
            return p|q;
        lc[p]=merge(lc[p],lc[q]);
        rc[p]=merge(rc[p],rc[q]);
        return p;
    }
    int erfen(int o,int l,int r,int x)
    {
        if(!o)
            return INF;
        if(x>r)
            return INF;
        if(l==r)
            return l;
        int md=l+r>>1,k;
        if((k=erfen(lc[o],l,md,x))^INF)
        	return k;
        return erfen(rc[o],md+1,r,x);
    }

};
template<int N,int M> struct graph{
    struct edge{
        int v,nxt;
    }e[M];
    int hd[N],e_num;
    void add_edge(int u,int v)
    {
        e[++e_num]=(edge){v,hd[u]};
        hd[u]=e_num;
    }
};
template<int N>struct SAM{
    int tr[N<<1][27],l[N<<1],fil[N<<1][21],idx=1,ls=1,g[N],rt[N<<1];
    segment<N*60> s;
    graph<N<<1,N<<1>t;
    void insert(int s)
    {
        int k=++idx,p=ls;
        g[l[k]=l[ls]+1]=k,ls=k;
        SAM::s.update(rt[k],1,2*n+1,l[k]);
        while(p&&!tr[p][s])
            tr[p][s]=k,p=fil[p][0];
        if(!p)
            fil[k][0]=1;
        else
        {
            int q=tr[p][s];
            if(l[q]==l[p]+1)
                fil[k][0]=q;
            else
            {
                int nw=++idx;
                l[nw]=l[p]+1,fil[nw][0]=fil[q][0];
                memcpy(tr[nw],tr[q],sizeof(tr[0]));
                fil[q][0]=fil[k][0]=nw;
                while(p&&tr[p][s]==q)
                    tr[p][s]=nw,p=fil[p][0];
            }
        }
    }
    void dfs(int x)
    {
		for(int i=1;i<=20;i++)
			fil[x][i]=fil[fil[x][i-1]][i-1];
		for(int i=t.hd[x];i;i=t.e[i].nxt)
			dfs(t.e[i].v);
    }
    void build()
    {
		for(int i=2;i<=idx;i++)
			t.add_edge(fil[i][0],i);
        dfs(1);
    }
    void sou(int x)
    {
		for(int i=t.hd[x];i;i=t.e[i].nxt)
		{
			sou(t.e[i].v);
			rt[x]=s.merge(rt[x],rt[t.e[i].v]);
		}
		for(int i=0;i<q[x].size();i++)
		{
			int len=qu[q[x][i]].r-qu[q[x][i]].l,lst=qu[q[x][i]].s+len,c=0;
            LL sum=0;
            while(1)
            {
				int k=s.erfen(rt[x],1,n+n+1,lst);
				if(k>qu[q[x][i]].t)
					break;
				sum+=k-len,++c;
				lst=k+len+1;
            }
			ans[q[x][i]]=1LL*c*k-sum;
        }
    }
    void add(int r,int len,int x)
    {
		int k=g[r];
		for(int i=20;i>=0;i--)
			if(l[fil[k][i]]>=len)
				k=fil[k][i];
		q[k].push_back(x);
    }
};
SAM<N<<1>sm;
int main()
{
    scanf("%d%d%s%s%d",&n,&k,s+1,t+1,&TME);
    for(int i=1;i<=n;i++)
        sm.insert(s[i]-'a');
    sm.insert(26);
    for(int i=1;i<=n;i++)
	    sm.insert(t[i]-'a');
	sm.build();
    for(int i=1;i<=TME;i++)
    {
        scanf("%d%d%d%d",&qu[i].s,&qu[i].t,&qu[i].l,&qu[i].r);
        qu[i].id=i;
         if(qu[i].r-qu[i].l<=50)
             p[qu[i].r-qu[i].l].push_back(i);
         else
			sm.add(n+1+qu[i].r,qu[i].r-qu[i].l+1,i);
    }
	for(int i=0;i<=50;i++)
	{
		for(int i=1;i<=tme;i++)
			g[i].clear();
		tme=0;
		mp.clear();
		for(int j=1;j+i<=n;j++)
		{
			str="";
			for(int k=j;k<=j+i;k++)
				str.push_back(s[k]);
			if(!mp[str])
				mp[str]=++tme;
			g[mp[str]].push_back(j);
		}
		for(int i=0;i<=n+1;i++)
			for(int j=0;j<20;j++)
				nx[i][j]=n+1,ns[i][j]=0;
		for(int j=1;j<=tme;j++)
		{
			for(int k=0;k<g[j].size();k++)
			{
				vector<int>::iterator it=upper_bound(g[j].begin(),g[j].end(),g[j][k]+i);
				if(it!=g[j].end())
					ns[g[j][k]][0]=nx[g[j][k]][0]=*it;
			}
		}
		for(int i=n;i>=0;i--)
			for(int j=1;j<20;j++)
				ns[i][j]=ns[i][j-1]+ns[nx[i][j-1]][j-1],nx[i][j]=nx[nx[i][j-1]][j-1];
 		for(int j=0;j<p[i].size();j++)
		{
			str="";
			for(int k=qu[p[i][j]].l;k<=qu[p[i][j]].r;k++)
				str.push_back(t[k]);
			if(mp[str])
			{
				int k=mp[str];
				vit it=lower_bound(g[k].begin(),g[k].end(),qu[p[i][j]].s);
				if(it!=g[k].end()&&(*it)+i<=qu[p[i][j]].t)
				{
					int nw=*it,ret=1;
					LL s=nw;
					for(int k=19;k>=0;k--)
						if(nx[nw][k]+i<=qu[p[i][j]].t)
							ret+=1<<k,s+=ns[nw][k],nw=nx[nw][k];
					ans[p[i][j]]=1LL*ret*::k-s;
				}
			}
		}
	}
    sm.sou(1);
    for(int i=1;i<=TME;i++)
        printf("%lld\n",ans[i]);
    return 0;
}