总体最小二乘法（Total Least Squares）拟合直线

前言

最小二乘法是最小化每个点到直线的垂直误差，由于误差采用的是垂直误差，导致越接近垂直线（平行于\(y\)轴），拟合效果越差，无法拟合垂直线。

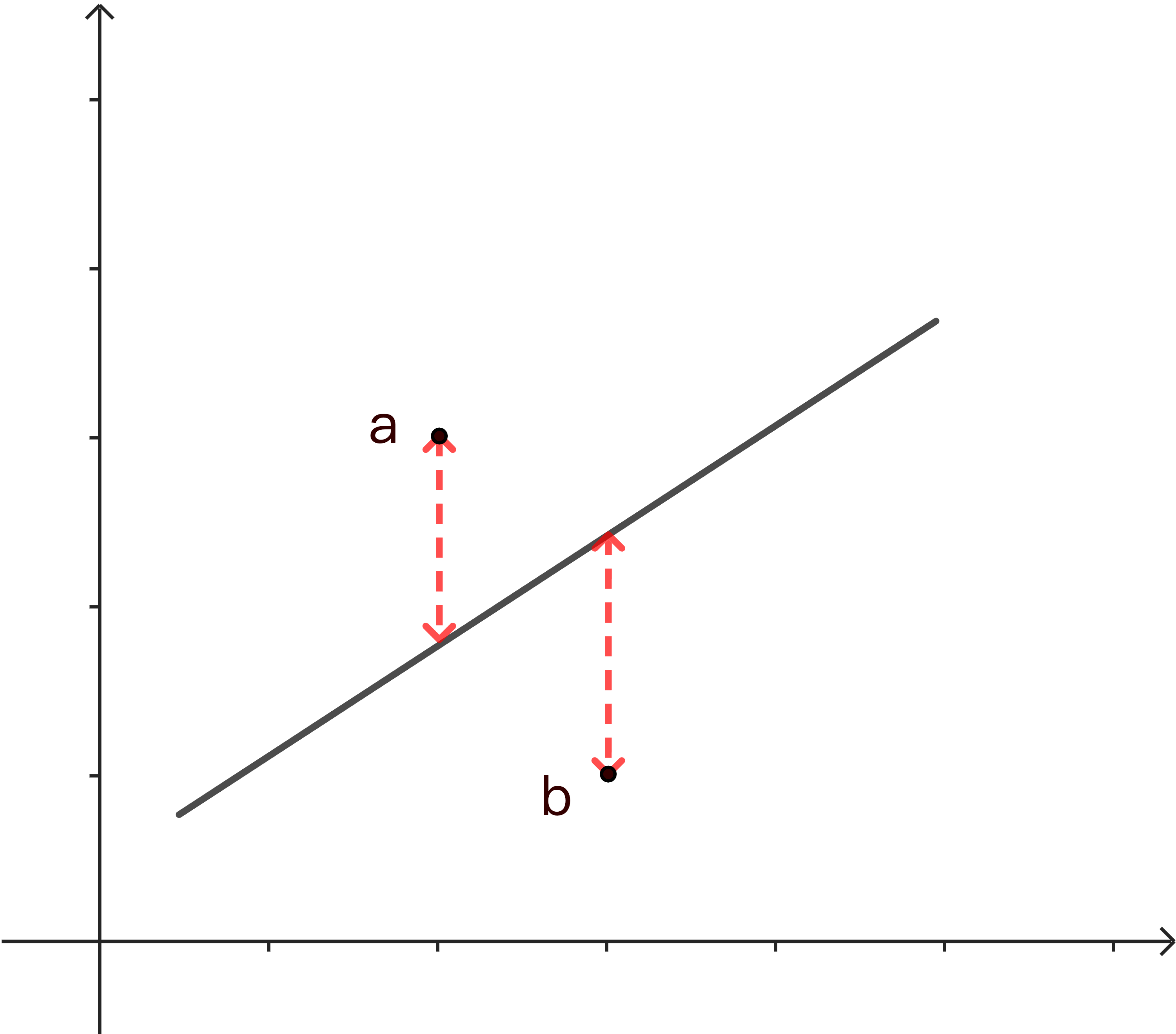
通过最小化每个点到直线的距离误差可以解决最小二乘法无法拟合垂直线的问题，也就是总体最小二乘法（Total Least Squares）。

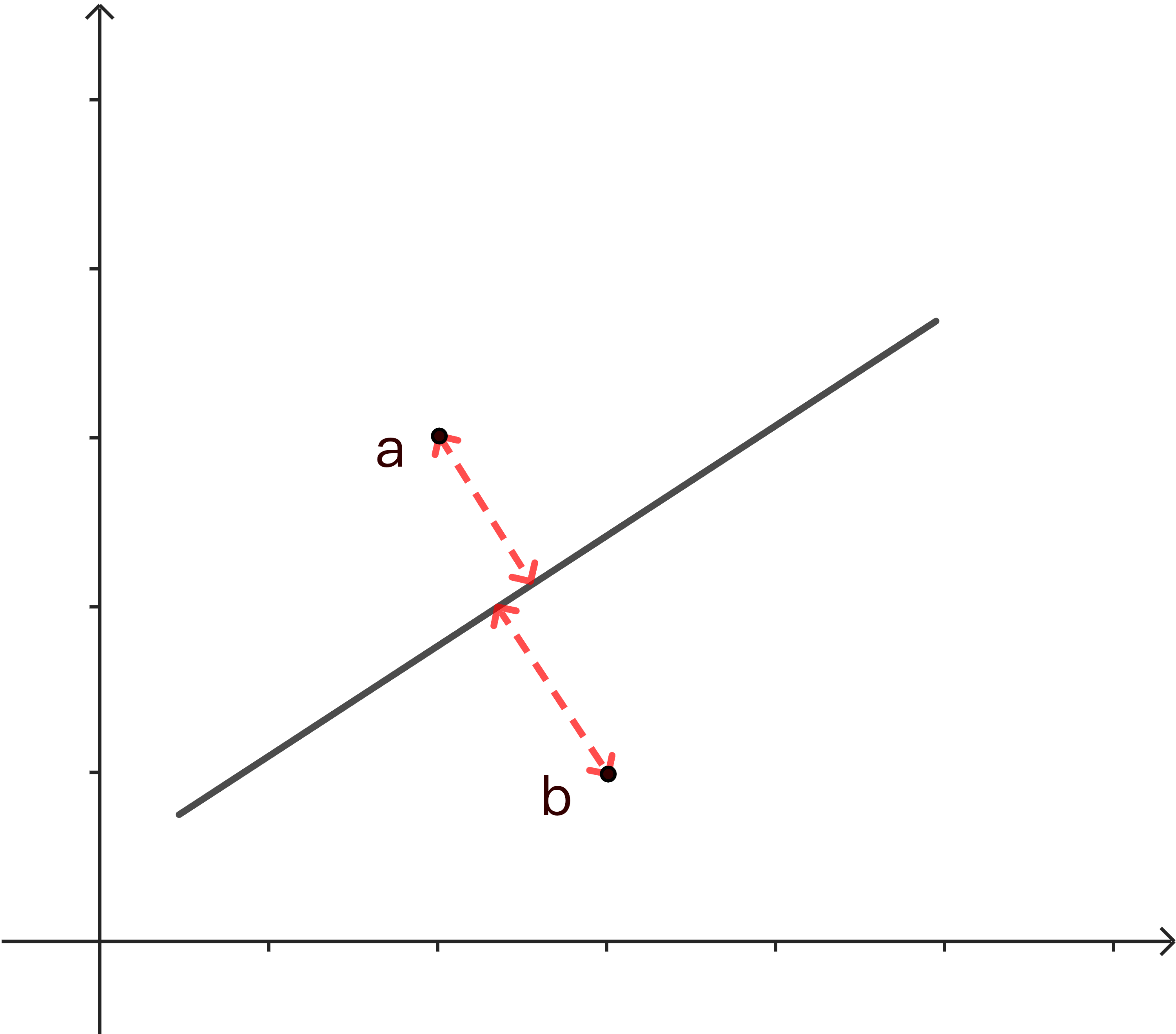
总体最小二乘法

将直线使用如下方程表示:

\[ax+by+c=0 \tag{1}
\]

点\((x_1, y_1)\)到直线的距离可以表示为：

\[\pmb{e} = \frac{|ax_1+bx_1+c|}{\sqrt{a^2+b^2}} \tag{2}
\]

假设\(a^2+b^2=1\)，那么点\((x_1, y_1)\)到直线的距离可以表示为：

\[\pmb{e} = |ax_1+by_1+c| \quad , \quad a^2+b^2=1 \tag{3}
\]

如果拟合直线的参数为\(a,b,c\)，点到拟合直线距离称为该点的拟合误差，给定\(n\)个点\((x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\)，那么直线的拟合方差为：

\[\begin{Vmatrix}\pmb{\sigma}\end{Vmatrix}^2=\frac{1}{n}\sum\limits_{i=1}^{i=n}{(ax_i+by_i+c)^2} \quad , \quad a^2+b^2=1 \tag{4} \label{4}
\]

方差最小时的\(a,b,c\)为直线的拟合参数。这里把方差记为\(\pmb{E}\)，即\(\pmb{E}=\begin{Vmatrix}\pmb{\sigma}\end{Vmatrix}^2\)。由于极值处的偏导为0，先对\(\pmb{E}\)求\(c\)的偏导：

\[\frac{\partial \pmb{E}}{\partial c}=\frac{2}{n}\sum\limits_{i=1}^{i=n}{\big(ax_i+by_i+c\big)}=0 \tag{5}
\]

得到：

\[c=-\frac{a}{n}\sum\limits_{i=1}^{i=n}x_i-\frac{b}{n}\sum\limits_{i=1}^{i=n}y_i=-a\overline{x}-b\overline{y} \tag{6}
\]

代入方差表达式\(\eqref{4}\)得：

\[\begin{align*}
\pmb{E} &=\frac{1}{n}\sum\limits_{i=1}^{i=n}{(ax_i+by_i-a\overline{x}-b\overline{y})^2} \tag{7} \\
&= \frac{1}{n}\sum\limits_{i=1}^{i=n}\Big({a(x_i-\overline{x})+b(y_i-\overline{y})}\Big)^2 \\

&=
\begin{Vmatrix}
\begin{bmatrix}
x_1-\overline{x} & y_1-\overline{y} \\
\vdots & \vdots \\
x_n-\overline{x} & y_n-\overline{y}
\end{bmatrix}
\begin{bmatrix}
a \\
b
\end{bmatrix}

\end{Vmatrix}^2 \\

&=\begin{Vmatrix}\pmb{Bz}\end{Vmatrix}^2
\end{align*}
\]

其中：

\[\pmb{B}= \begin{bmatrix}
x_1-\overline{x} & y_1-\overline{y} \\
\vdots & \vdots \\
x_n-\overline{x} & y_n-\overline{y}
\end{bmatrix} \tag{8}
\]

\[\pmb{z}=\begin{bmatrix}a\\b\end{bmatrix} \tag{9}
\]

由于\(a^2+b^2=1\)，即\(\pmb{z}^T\pmb{z}=1\)。可使用Lagrange乘法求解，目标函数为：

\[J(\pmb{z})=\begin{Vmatrix}\pmb{Bz}\end{Vmatrix}^2+\lambda\big(1-\pmb{z}^T\pmb{z}\big) \tag{10}
\]

式中\(\lambda\)为Lagrange乘数，由\(\frac{\partial J(\pmb{z})}{\partial \pmb{z}}=0\)，得到：

\[\pmb{B}^T\pmb{B}\pmb{z}=\lambda \pmb{z} \tag{11}
\]

可见\(\lambda\)和\(\pmb{z}\)分别为矩阵\(\pmb{B}^T\pmb{B}\)的特征值和特征向量。

\[\pmb{B}^T\pmb{B} = \begin{bmatrix}
\sum\limits_{i=1}^{i=n}\big(x_1-\overline{x}\big)^2
& \sum\limits_{i=1}^{i=n}\big(x_1-\overline{x}\big)\big(y_1-\overline{y}\big) \\
\sum\limits_{i=1}^{i=n}\big(x_1-\overline{x}\big)\big(y_1-\overline{y}\big) & \sum\limits_{i=1}^{i=n}\big(y_1-\overline{y}\big)^2
\end{bmatrix} \tag{12}
\]

可见矩阵\(\pmb{B}^T\pmb{B}\)为2阶矩阵，因此存在2个特征值和特征向量。\(\pmb{E}=\begin{Vmatrix}\pmb{Bz}\end{Vmatrix}^2=\pmb{z}\pmb{B}^T\pmb{B}\pmb{z}=\pmb{z}^T\lambda\pmb{z}=\lambda\)的最小值为矩阵\(\pmb{B}^T\pmb{B}\)最小的特征值，而直线拟合参数\(a,b\)为最小特征值对应的特征向量。

参考文档

1. 计算机视觉入门-最小二乘法、随机取样法、鲁棒估计、霍夫变换
2. 矩阵分析与应用（第2版）张贤达
3. 直线拟合——最小二乘法、hough变换