[Codeforces]906D Power Tower
虽说是一道裸题,但还是让小C学到了一点姿势的。
Description
给定一个长度为n的数组w,模数m和询问次数q,每次询问给定l,r,求:
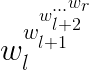
对m取模的值。
Input
第一行两个整数n,m,表示数组长度和模数。
接下来一行n个数,表示w数组。
接下来一行一个整数q,表示询问次数。
接下来q行,每行两个整数l,r,表示一次询问。
Output
对于每次询问,输出一行一个整数表示答案。
Sample Input
6 1000000000
1 2 2 3 3 3
8
1 1
1 6
2 2
2 3
2 4
4 4
4 5
4 6
Sample Output
1
1
2
4
256
3
27
597484987
HINT
1 ≤ n ≤ 105,1 ≤ m ≤ 109,1 ≤ wi ≤ 109,1 ≤ q ≤ 105,1 ≤ l ≤ r ≤ n。
Solution
看到这么清奇的式子,你大概会第一时间想到降幂大法吧?
先说说扩展欧拉定理,对于任意正整数a,b,p:
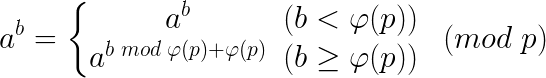
所以假设堆叠的幂次足够大,那么式子就可以转化为:


已知p经过至多2log次phi就会变成1。
所以递归求解,至多走到2log层模数就会变成1,所以返回0就行。
所以这道题就非常显然了,首先预处理出m的所有phi,对于每个询问,从l开始直接递归暴力,直到模数为1时返回。
还有一个问题,在求a^b%p的时候,怎么比较b和phi(p)的大小呢?
一种思路就是暴力计算a的后log项的值,注意还要特判1的情况,但这样写起来确实麻烦。
当然,有一种非常精妙的取模写法:
int modulo(ll x,int mod) {return x<mod?x:x%mod+mod;}
这是在做什么呢?这就是在比较b和phi(p)的大小,如果b<phi(p),返回b;否则返回b%phi(p)+phi(p)。
然后原式就变成了这样:

这样做看上去漏洞百出,可能的情况是,原本我们要计算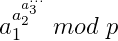 ,其中
,其中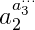 大等于
大等于 。
。
然而我们计算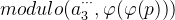 ,将
,将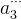 取模后,却发现
取模后,却发现 小于
小于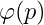 了。
了。
是否有这种可能呢?
其实就相当于判断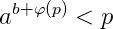 是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
所以我们来看一看 是否有可能成立。
是否有可能成立。
有可能。
当且仅当p=6时,不等式成立。
然而6有什么特殊的性质呢?
我们发现phi(x)=6只有三个解:x=7,x=9或x=18。
所以接下来我们只要证明 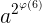 和
和 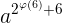 即
即 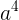 和
和 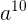 在对x取模的意义下相等即可。(其中phi(x)=6)
在对x取模的意义下相等即可。(其中phi(x)=6)
若a为x的倍数,显然它们对x取模都等于0,对于答案无影响。
当x=7时, ,所以
,所以 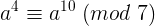 ;
;
当x=9时,若 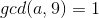 ,则影响同上;
,则影响同上;
若 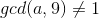 ,一定有
,一定有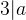 ,所以一定有
,所以一定有  ,
,
所以一定有 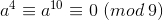 ,对于答案是没有影响的;
,对于答案是没有影响的;
当x=18时,若 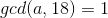 或
或 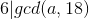 ,则影响同上;
,则影响同上;
我们有一个显然的结论:同余方程 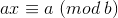 的解为
的解为 
若 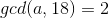 ,则
,则 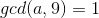 ,则
,则  ,则
,则 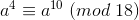
若 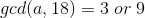 ,则
,则  且
且 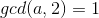 ,则
,则 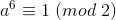 ,则
,则 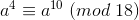
所以综上,我们就证明了该算法的正确性。
时间复杂度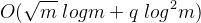 。
。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define MN 100005
using namespace std;
int a[MN],mod[MN];
int n,p;
bool fg; inline int read()
{
int n=,f=; char c=getchar();
while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
while (c>='' && c<='') {n=n*+c-''; c=getchar();}
return n*f;
} inline int pro(ll x,int md) {return x<md?x:x%md+md;}
inline int mi(int x,int y,int md)
{
register int z=;
for (;y;x=pro(1LL*x*x,md),y>>=)
if (y&) z=pro(1LL*z*x,md);
return z;
} int dfs(int x,int y,int lim)
{
if (x==lim) return a[x]>=mod[y]?a[x]%mod[y]+mod[y]:a[x];
if (mod[y]==) return ;
return mi(a[x],dfs(x+,y+,lim),mod[y]);
} int main()
{
register int i,j,x,y;
n=read(); mod[]=read();
for (i=;mod[i]>;++i)
{
mod[i+]=x=mod[i];
for (j=;j*j<=x;++j)
{
for (fg=;x%j==;x/=j,fg=true);
if (fg) mod[i+]=1LL*mod[i+]*(j-)/j;
}
if (x>) mod[i+]=1LL*mod[i+]*(x-)/x;
}
for (i=;i<=n;++i) a[i]=read();
for (p=read();p;--p)
{
x=read(); y=read();
printf("%d\n",dfs(x,,y)%mod[]);
}
}
Last Word
打Codeforces的时候正纳闷这种情况该怎么处理,却发现大佬们清一色都是这么写的。
小C觉得自己的证明蠢得不行啊……
如果读者有更直观的证明该算法的正确性的方法请务必告诉小C。
[Codeforces]906D Power Tower的更多相关文章
- CodeForces - 906D Power Tower(欧拉降幂定理)
Power Tower CodeForces - 906D 题目大意:有N个数字,然后给你q个区间,要你求每一个区间中所有的数字从左到右依次垒起来的次方的幂对m取模之后的数字是多少. 用到一个新知识, ...
- Codeforces 906D Power Tower(欧拉函数 + 欧拉公式)
题目链接 Power Tower 题意 给定一个序列,每次给定$l, r$ 求$w_{l}^{w_{l+1}^{w_{l+2}^{...^{w_{r}}}}}$ 对m取模的值 根据这个公式 每次 ...
- Codeforces Round #454 (Div. 1) CodeForces 906D Power Tower (欧拉降幂)
题目链接:http://codeforces.com/contest/906/problem/D 题目大意:给定n个整数w[1],w[2],……,w[n],和一个数m,然后有q个询问,每个询问给出一个 ...
- [CodeForces - 906D] Power Tower——扩展欧拉定理
题意 给你 $n$ 个 $w_i$ 和一个数 $p$,$q$个询问,每次询问一个区间 $[l,r] $,求 $w_l ^{w_{l+1}^{{\vdots}^{w_r}}} \ \% p$ 分析 由扩 ...
- CodeForces 907F Power Tower(扩展欧拉定理)
Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is u ...
- 【CodeForces】906 D. Power Tower 扩展欧拉定理
[题目]D. Power Tower [题意]给定长度为n的正整数序列和模数m,q次询问区间[l,r]累乘幂%m的答案.n,q<=10^5,m,ai<=10^9. [算法]扩展欧拉定理 [ ...
- Codeforces Round #454 D. Power Tower (广义欧拉降幂)
D. Power Tower time limit per test 4.5 seconds memory limit per test 256 megabytes input standard in ...
- CodeForces 906D (欧拉降幂)
Power Tower •题意 求$w_{l}^{w_{l+1}^{w_{l+2}^{w_{l+3}^{w_{l+4}^{w_{l+5}^{...^{w_{r}}}}}}}}$ 对m取模的值 •思路 ...
- [CodeForces - 1225D]Power Products 【数论】 【分解质因数】
[CodeForces - 1225D]Power Products [数论] [分解质因数] 标签:题解 codeforces题解 数论 题目描述 Time limit 2000 ms Memory ...
随机推荐
- 【iOS】跳转到设置页面
iOS8.0以后有效 定位服务 定位服务有很多APP都有,如果用户关闭了定位,那么,我们在APP里面可以提示用户打开定位服务.点击到设置界面设置,直接跳到定位服务设置界面.代码如下: 1 2 3 4 ...
- 老板怎么办,我们网站遭到DDoS攻击又挂了?
相信现在正在阅读此文的你,一定听说过发生在上个月的史上最大的DDoS攻击. 美国东部时间2月28日,GitHub在一瞬间遭到高达1.35Tbps的带宽攻击.这次DDoS攻击几乎可以堪称是互联网有史以来 ...
- Python 迭代器之列表解析与生成器
 [TOC] 1. 列表解析 1.1 列表解析基础 列表解析把任意一个表达式应用到一个迭代对象中的元素 Python内置ord函数会返回一个字符的ASCII整数编码(chr函数是它的逆过程, 它将A ...
- H5新特性之webWorker
众所周知javascript是单线程语言,这就是js开发难度较低的原因了,因为不需要解决多线程的资源共享问题(例如死锁),但是单线程性能并不好,因此多了一个webWorker实现js的多进程来提升js ...
- 谈谈ASP.NET Core中的ResponseCaching
前言 前面的博客谈的大多数都是针对数据的缓存,今天我们来换换口味.来谈谈在ASP.NET Core中的ResponseCaching,与ResponseCaching关联密切的也就是常说的HTTP缓存 ...
- vue组件详解(三)——组件通信
组件之间通信可以用下图表示: 组件关系可分为父子组件通信.兄弟组件通信.跨级组件通信. 一.自定义事件 当子组件需要向父组件传递数据时,就要用到自定义事件. 子组件用$emit ()来触发事件,父组件 ...
- Apollo单向SSL认证(1)
参考链接:https://www.cnblogs.com/benwu/articles/4891758.html keytool -genkey -alias mybroker -keyalg RSA ...
- Docker学习笔记 - Docker的数据卷容器
一.什么是数据卷容器 如果你有一些持续更新的数据需要在容器之间共享,最好创建数据卷容器. 数据卷容器:用于容器间的数据共享,主动挂载宿主机目录,用于其他容器挂载和共享. 二.数据卷容器的操作 1.创建 ...
- django的models模型类的常用数据类型和选项
django框架的models模块ORM框架,能够让我们通过编写类的方式,帮助我们自动生成数据库表. 生成的数据库表名为 应用模块名称_类名 数据库表中字段名 如果我们没有在参数中指定,就是我们写的类 ...
- leetcode算法: Keyboard Row
Given a List of words, return the words that can be typed using letters of alphabet on only one row' ...
