wqs二分

今天模拟赛有一道林克卡特树，完全没有思路

赛后想了一想，不就是求\(k+1\)条不相交的链，使其权值之和最大嘛，傻了。

有一个最裸的\(DP\)，设\(f[i][j][k]\)表示在以\(i\)为根的子树中，选了\(j\)条链，\(k=0\)表示\(i\)不在链上，\(k=1\)表示\(i\)是链的一端，\(k=2\)表示\(i\)在链的中间

这样就随便转移了，就是个\(O(nk^2)\)的树上背包

然后呢，又傻了，这能怎么优化？

我先在这里Orz一下大佬BLUESKY007，没有学过wqs二分，发现了\(f\)数组关于\(k\)的单调性，一波二分直接A了 %%%%%%

没错，我们需要用这个单调性来进行优化。据官方题解称，假设你闲着没事，把\(k=0-100\)的表打了一下，你就会发现这个上凸函数，但是如果并没有闲心，那我们就大胆的猜一下。

当\(k\)很小的时候，我们肯定先删负权边，这样最大权值和就增大了。当负权边不够用了怎么办，我们就只能开始删正权边，这种情况貌似比较复杂，先来看看正权边删的很多的情况。随着正权边越删越多，最大权值和肯定有一个下降的趋势，这样随着\(k\)的增大，\(f\)就呈现出一个先增后减的趋势，也许\(f\)是一个上凸函数？猜对啦，确实是的

接下来我们需要一个叫wqs二分的优化方法，它经常被用于这样的问题：有\(n\)个带权物品，用满足一定限制的方法选\(m\)个，使得其权值和取最值，而且权值和的最值是关于\(m\)的凸函数。设在取\(x\)个物品时的权值和为\(f(x)\)，那么\(f(x)\)的图像大概长这个样子：



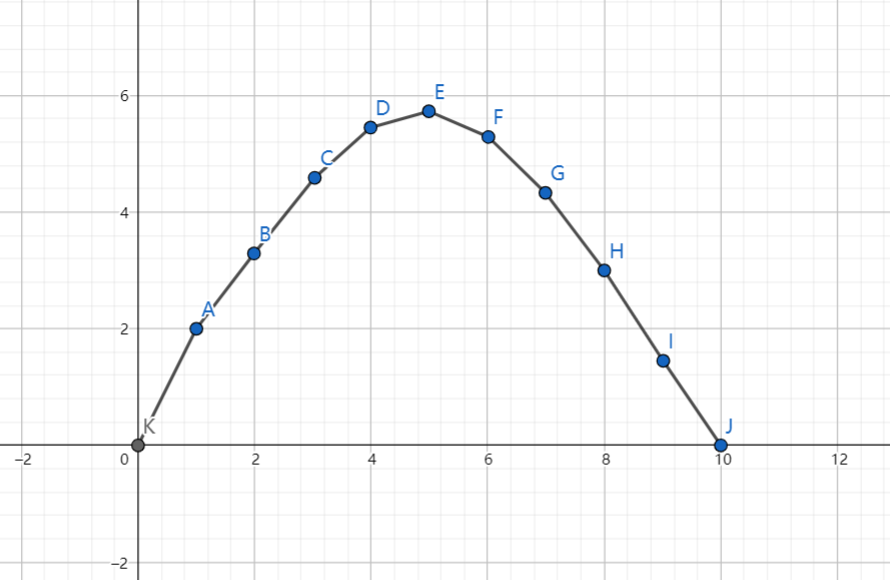
那我们该怎么知道\(f(m)\)呢，因为\(f(x)\)是凸的，考虑用一条直线去切它。就像这样：



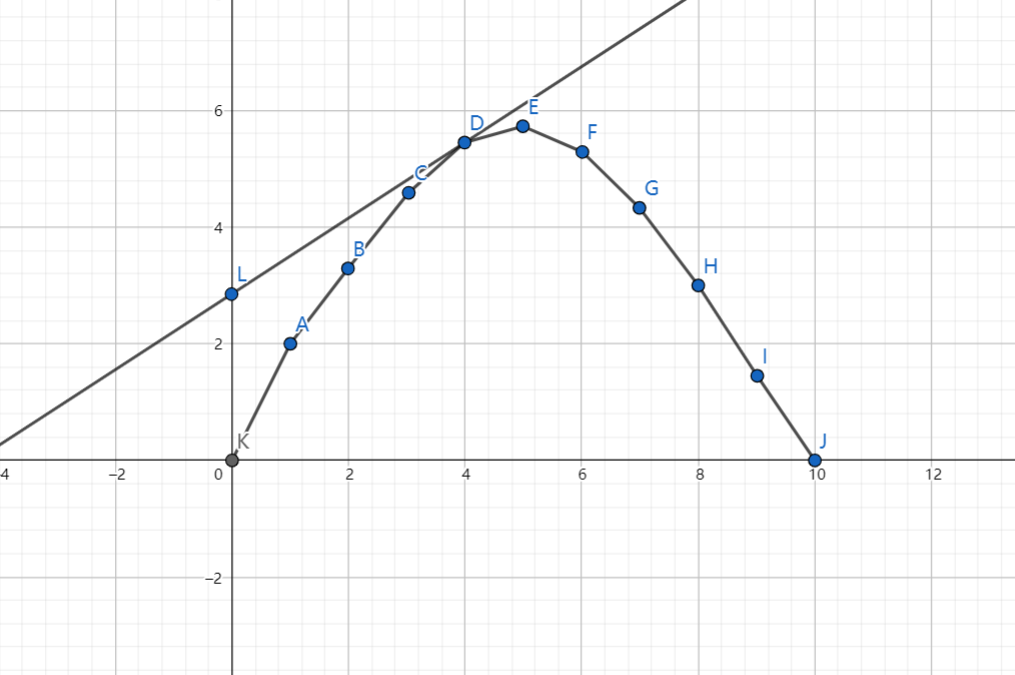
这样我们就得到了一条斜率为\(k\)，解析式为\(y=kx+b\)的直线，上下移动这条直线，你会发现在切点处的截距\(b\)是最大的：



而且切点处\(b=f(x)-kx\)，假设我们能找到最大的\(b\)并顺便记录切点的位置，不就能计算\(f(x)\)的值了吗？观察\(b\)的表达式，发现如果我们给每个物品加上一个附加权值\(-k\)，然后求出来的最大权值\(f'(x)\)和\(f(x)-kx\)是等价的，于是\(b_{max}=max\{f'(x)\}\)，这个式子没有数量限制，直接\(DP\)就行了，中间顺便记录最佳决策点\((x_{max},b_{max})\)。这样的话，就能算出来\(f(x)=kx_{max}+b_{max}\)。用因为我们知道了\(x_{max}\)，拿它跟\(m\)比较，就知道是该增大还是减小斜率\(k\)，这也提示了我们可以二分斜率

还有一个比较重要的细节，就是\(b\)的最佳决策点可能不止一个，也就是说当前的这条直线跟图像有多个切点，这样我们便无法得知\(m\)在左边还是右边了。我们可以通过一个策略来解决这个问题，就是取\(x\)最大的最佳决策点，最后直接把\(x_{max}\)带入求出\(f(m)\)就行了

以下是帮助你取得大师之剑的代码（滑稽）：

#include <bits/stdc++.h>

using namespace std;

//dp+wqs二分
//首先把问题转化为求树上k+1条不相交路径，使其权值和最大

#define N 300000
#define ll long long
#define INF 10000000000000 //INF不能太大，也不能太小

int n, k, eid, head[N+5];
ll m;

struct Edge {
  int next, to, w;
}e[2*N+5];

struct DP { //为了方便重载了运算符
  ll v;
  int cnt;
  DP operator + (DP rhs) {
    return DP{v+rhs.v, cnt+rhs.cnt};
  }
  bool operator < (DP rhs) const {
    return v < rhs.v || (v == rhs.v && cnt < rhs.cnt);
  }
}f[3][N+5], temp;

void addEdge(int u, int v, int w) {
  e[++eid].next = head[u];
  e[eid].to = v;
  e[eid].w = w;
  head[u] = eid;
}

DP Max(int u) {
  return max(f[0][u], max(f[1][u], f[2][u]));
}

DP newDP(DP &a, ll v0, int cnt0) {
  return DP{a.v+v0, a.cnt+cnt0};
}

void dp(int u, int fa) {
  f[0][u] = DP{0, 0}, f[1][u] = DP{-INF, 0}, f[2][u] = DP{-m, 1};
  int i, v, w;
  for(i = head[u]; i; i = e[i].next) {
    v = e[i].to, w = e[i].w;
    if(v == fa) continue;
    dp(v, u);
    temp = Max(v);
    f[2][u] = max(f[2][u]+temp, f[1][u]+max(newDP(f[0][v], w, 0), newDP(f[1][v], w+m, -1)));
    f[1][u] = max(f[1][u]+temp, f[0][u]+max(newDP(f[0][v], w-m, +1), newDP(f[1][v], w, 0)));
    f[0][u] = f[0][u]+temp;
  }
}

void check() {
  dp(1, 0);
}

int main() {
  scanf("%d%d", &n, &k); k++;
  for(int i = 1, x, y, z; i <= n-1; ++i) {
    scanf("%d%d%d", &x, &y, &z);
    addEdge(x, y, z), addEdge(y, x, z);
  }
  ll l = -INF, r = INF, ans; //二分斜率
  while(l <= r) {
    m = (l+r)>>1;
    check();
    if(Max(1).cnt < k) r = m-1;
    else l = m+1, ans = m;
  }
  m = ans;
  check();
  printf("%lld\n", Max(1).v+ans*k);
  return 0;
}

再附一道例题

CF739E. Gosha is hunting

题解在这里