SVD的几何意义，以及在去噪，推荐系统中的应用

很多文章说到奇异值分解的时候总是大概罗列下它的功能，并没有对功能及物理意义进行过多的阐述，现在我来对奇异值进行整理一下。

一 奇异值分解

对任意的矩阵A∈Fmn，rank(A)=r(矩阵的秩)，总可以取A的如下分解：，其中U和V是正交矩阵。分别为左右奇异值向量。

U是m×m阶酉矩阵；Σ是m×n阶非负实数对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σii即为M的奇异值。

V的列（columns）组成一套对M的正交"输入"或"分析"的基向量。这些向量是M*M的特征向量。

U的列（columns）组成一套对M的正交"输出"的基向量。这些向量是MM*的特征向量。

Σ对角线上的元素是奇异值，可视为是在输入与输出间进行的标量的"膨胀控制"。这些是M*M及 MM*的特征值的非零平方根，并与U和V的行向量相对应。

观察一个4×5的矩阵

M矩阵的奇异值分解如下UΣV ^*

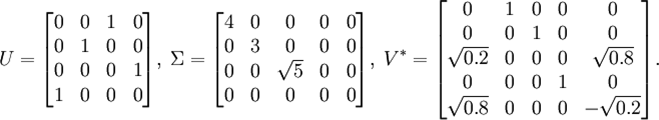
。矩阵U和V ^* 都是酉矩阵，它们乘上各自的共轭转置都等于单位矩阵。如下所示。在这个例子中，由于U和V ^* 都是酉矩阵，所以他门都是正交矩阵。

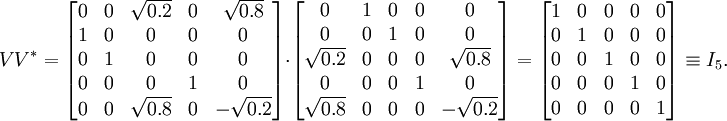
　由于Σ有一个对角元素是o，所以这个奇异值分解不是唯一的。例如，例如V使得

能得到M的另一个奇异值分解。

二 奇异值分解的几何意义

研究将一个空间映射到不同空间，特别是不同维数的空间时候，例如超定或欠定方程组所表示的情况，就需要用矩阵的奇异值来描述算子对空间的作用了。

现在给定一个二维平面上的单位圆，在映射A的变化下（矩阵可以看成一种线性变化）

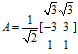
Matlab程序：

结果：

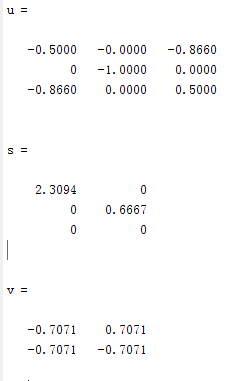
V是一个正交矩阵，我们现在让他把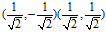变化一下：（其实V就是一个简简单单的旋转，没有涉及到维数的变换）

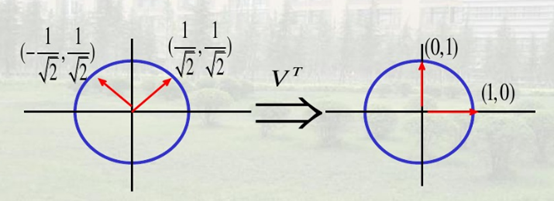
S是一个3x2矩阵，他自然也是一种变化：

由上面可以看出，s是将原来的坐标进行拉长奇异值倍。而最后的（0,0表示原点坐标），变化如图：

其实S就是将平面上的单位圆拉升到三维空间上的椭圆。

U是一个3x3的矩阵，自然表示在三维空间的旋转了。如下图：

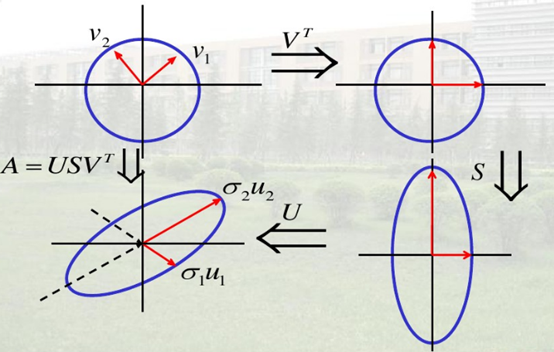
总结：若X是n维单位球面上的一点，则Ax是一个n维椭圆面上的点，其中椭圆的n个半轴上正好是A的n个奇异值。

简而言之：在二维空间下，奇异值将单位圆变成了椭圆。两个奇异值正好是椭圆的长轴和短轴。逆向，不就实现了降维了么？

三 奇异值在图形降噪方面的应用

如果我们单纯的用奇异值对一个矩阵图片进行奇异值分解，然后取其所有奇异值，那么这个过程是不会损失能量的，但是如果我们有意识的去除后面奇异值非常小的部分（奇异值默认是从大到小往下排列的）是不是就会损失一部分能量，有的人会问我，这个和降噪有什么必然的联系吗。

废话，当然有了，要不我写这个干吗。

废话不多说，先上matlab程序：

clear all;

close all;

clc;

a=imread('D:\Documents\MATLAB\shuaige.png');%本人帅照

%a=mat2gray(a)

a= rgb2gray(a);%灰度处理

imshow(mat2gray(a))%显示原图

[m,n]=size(a);

a=double(a);%把a里的数搞成双精度浮点型

r=rank(a);%求秩

[s,v,d]=svd(a);%对图片进行svd分解

%re=s*v*d';

，可以改变V和d的值，以便选取奇异值

figure;

imshow(mat2gray(re));%显示图片

imwrite(mat2gray(re),'1.jpg')

当我们直接对图片灰度化处理：（很明显，依然那么那么帅，哈哈）

现在我们取最大的那个奇异值得出的照片：（我屮艸芔茻，这什么生物，懵逼.GIF）

个最大的奇异值得出的照片：（帅气初现，有木有？哈哈）

试一试？（我这张帅照最大只能取到179）：（perfect）

总结：我们总是认为噪声都是那些奇异值特别小的点造成的，这样我们设置一个阀值θ，如果奇异值大于θ，我们就取θ，否则就省略之，这样是不是就对矩阵进行降噪的了？

四 奇异值分解在推荐系统的应用

我知道我写的一定没有我下面上传的好，所以我选择上传。。。。。

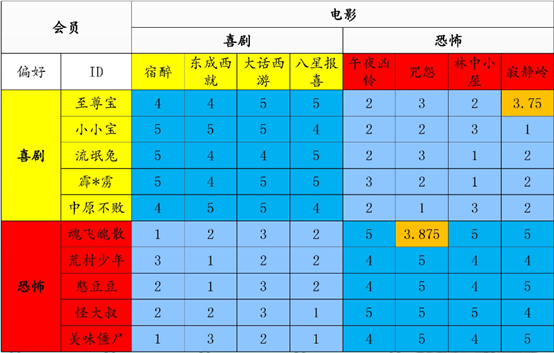
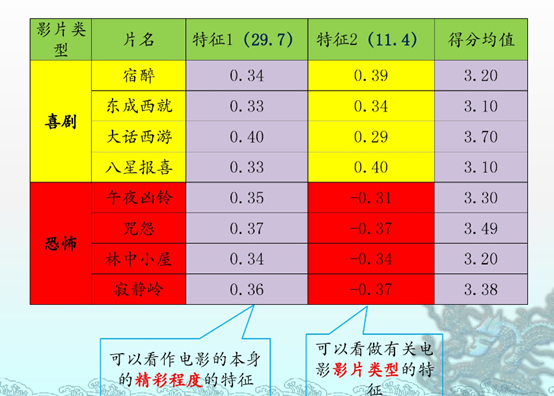
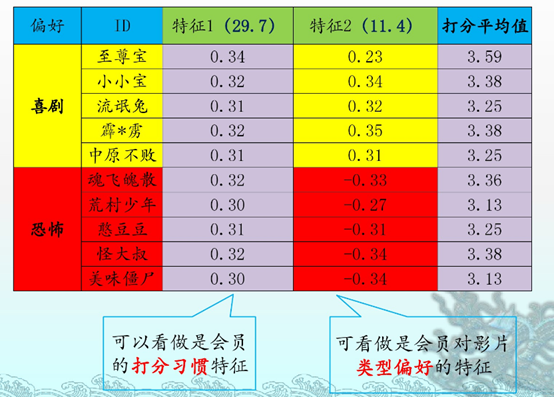
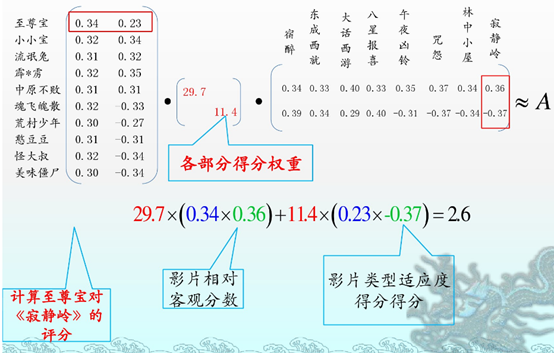
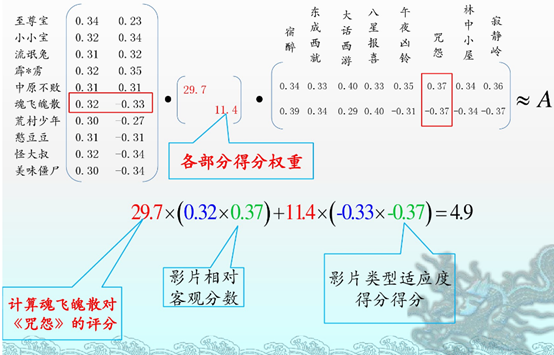
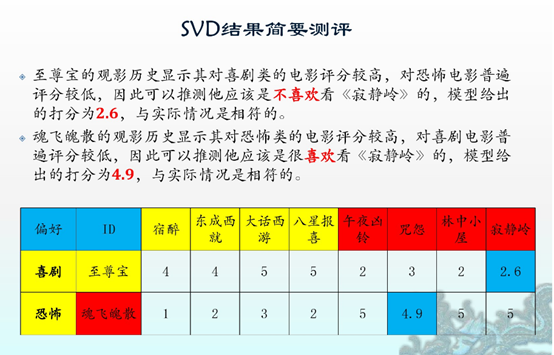
浅显易懂。拿来主义一波。

原文链接：http://wenku.baidu.com/view/6bbc396633687e21ae45a910

谢谢大家