mac/Linux源码安装TensorFlow

因为用pip命令直接下载安装会链接到google，导致打不开，比如使用pip install tensorflow碰到如下的问题。因此在本文中，主要介绍了如何通过源码进行TensorFlow的安装

$ pip install tensorflow
Collecting tensorflow
  Could not find a version that satisfies the requirement tensorflow (from versions: )
No matching distribution found for tensorflow

1、下载TensorFlow

可以将TensorFlow安装包下载到本地，可以根据自己的需求点击TensorFlow下载地址下载最新版本。例如下载最新版本的TensorFlow1.4.1.tar.gz，然后解压。

或者直接使用如下命令获取：

git clone --recurse-submodules https://github.com/tensorflow/tensorflow

使用 --recurse-submodules 选项来获取 TensorFlow 需要依赖的 protobuf 库文件。

2、安装Bazel

Bazel是Google开源构建工具，类似于Make的工具，用来编译构建tensorflow，mac的bazel安装指导

Bazel下载地址：
https://github.com/bazelbuild/bazel/releases（bazel-0.2.2b-installer-linux-x86_64.sh）

brew install bazel

如果安装成功，请用下面的命令查看：

bazel version

 3、安装TensorFlow

进入TensorFlow的文件夹下面进行相关的配置：

./configure

进行配置，在配置过程中会出现一系列的问题，通常情况下没有特殊的要求，一般全部都选择n：

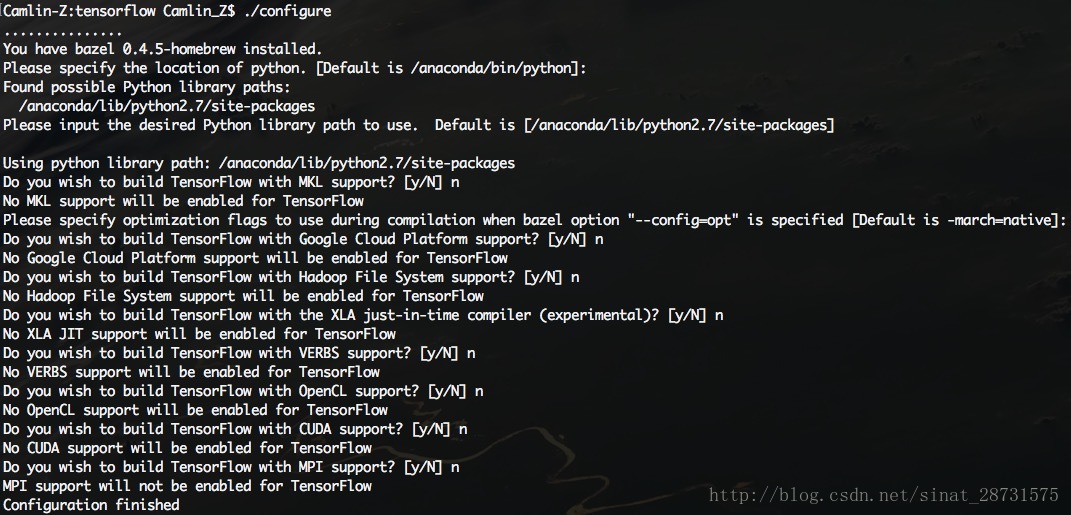
配置完成后就是编译过程了，输入终端命令，这个过程会花一段时间来编译，大概需要1个小时

$ bazel build --config=opt //tensorflow/tools/pip_package:build_pip_package

经过漫长的编译后，任务就基本上完成了，接下来就是输入下面的命令来生成pip安装包了：

$ bazel-bin/tensorflow/tools/pip_package/build_pip_package /tmp/tensorflow_pkg

最后就是用pip命令来安装TensorFlow了，注意/tmp/tensorflow_pkg/文件夹下的文件tensorflow-1.4.0-cp36-cp36m-macosx_10_7_x86_64.whl是自动生成的，跟安装的版本有关。

$ sudo pip install /tmp/tensorflow_pkg/tensorflow-1.4.-cp36-cp36m-macosx_10_7_x86_64.whl 

至此全部完成

4、测试

通过在python中加载TensorFlow模型进行测试是否安装完成。

>>> import tensorflow as tf
>>> 

也可以到tensorflow的sample里面跑教程

$ cd tensorflow/models/image/mnist
$ python convolutional.py

参考文档：

1、tensorflow源代码方式安装

2、Installing Bazel on macOS

3、TensorFlow的github上的源代码下载

4、TensorFlow源码安装

5、Mac下使用源码编译TensorFlow

6、如何在Mac电脑上面编译GPU版本TensorFlow