FFT 快速傅里叶变换

前言

lmc,ikka,attack等众多大佬都没教会的我终于要自己填坑了。

又是机房里最后一个学fft的人

用处

多项式乘法

卷积

\(g(x)=a_0+a_1x+a_2x^2\)

\(f(x)=b_0+b_1x+b_2x^2\)

他们的乘积c(x)就是

\(c(x)=a_0b_0+a_0b_1x+a_0b_2x^2+a_1b_0x+a_1b_1x^2+a_1b_2x^3+a_2b_0x^2+a_2b_1x^3+a_2b_2x^4\)

c(x)叫做g(x)和f(x)的卷积

就是定义了一个多项式的乘法操作

\(O(n^2)\)这样子写（还是代码明了）

    n=read(),m=read();

	for(int i=0;i<=n;++i) a[i]=read();

	for(int i=0;i<=m;++i) b[i]=read();

	for(int i=0;i<=n;++i)

		for(int j=0;j<=m;++j)

			c[i+j]+=a[i]*b[j];

	for(int i=0;i<=n+m;++i) printf("%d ",c[i]);

0x01

太慢了！！！

所以我们要用FFT进行优化，复杂度会降为\(O(nlogn)\)

多项式表示法

我们常用的是系数表示法，就是上文中用到的。

\(f(x)=a_0+a_1x+a_2x^2\)

现在我们学习新的表示法，点值法。

顾名思义，就是{x,f(x)}，然后我们只需要n+1的不同组就可以唯一确定一个多项式f(x)了，想一下高斯消元。

一些定义

多项式由系数表示法转为点值表示法的过程，就成为DFT。

相对地，把一个多项式的点值表示法转化为系数表示法的过程，就是IDFT。

而FFT就是通过取某些特殊的x的点值来加速DFT和IDFT的过程。

复数的定义及其运算

复数由实数和虚数组成

虚数可以表示为i*x,其中\(i=\sqrt{-1}\)

复数的表示形式有四种。

代数形式：\(z=a+bi,a,b\in R\)

几何形式：代数形式与复平面上的点\((a,b)\)或者向量\(\vec{OZ}\)一一对应

三角形式：\(z=r(cos\theta+isin\theta)，r\geq0,\theta\in R\)

指数形式：\(z=re^{i\theta}，r\geq0,\theta\in R\)

何为复平面，就是笛卡尔坐标系，横轴为实数，纵轴为虚数。

欧拉公式：\(e^{i\theta}=cos\theta+isin\theta\)

r为模长（长度），\(\theta\)为辅角(角度)

乘法

\((a+bi)(c+di)=(ac-bd)+(bc+ad)i\)

长度相乘，角度相加

\((r_1,\theta_1)*(r_2,\theta_2)=(r_1r_2,\theta_1\theta_2)\)

单位根

一个n等分的单位圆

上面每一份的那个点为\(w_n^i\)

attack的图真好看

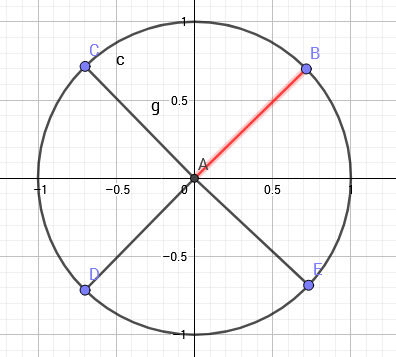
至于为何要扯复数单位根，就是因为它有一些美妙的性质可以降低我们的复杂度。

性质1

\(w_n^k=w_{2n}^{2k}\)

性质2

\(w_n^{2k}=-w_n^k\)

性质3

\(w_n^n=1\)或者\(w_n^{kn+m}=w_n^{m}\)

这些性质都可以套用欧拉公式\((e^{i\theta}=cos\theta+isin\theta)\)证明

或者 {

1、表示的都是一个点。

2、关于原点对称。

3.显然，或者说以n为循环节

}

FFT

分治！！

\(f(x)=a_0+a_1x+a_2x^2\)

n为偶数

把它按照奇偶分成两个等幂的多项式。

\(f(x)=a_0+a_1x+a_2x^2+a_3x^3\)

设\(a(x)=a_0+a_2x\)，\(b(x)=a_1+a_3x\)

那么\(f(x)=a(x^2)+xb(x^2)\)

我们依次带入\(w_n^k\),算出来\(f(w_n^k)\)，复杂度依旧O(n^2)

但是我们还有性质没用

假设\(k<\frac{n}{2}\)，现在要把\(x=ω_k^n\)代入f(x)

\(f(x)=a((w_n^k)^2)+w_n^kb((w_n^k)^2)\)

\(f(x)=a(w_n^{2k})+w_n^kb(w_n^{2k})\)

\(f(x)=a(w_{\frac{n}{2}}^{k})+w_n^kb(w_{\frac{n}{2}}^{k})\)

我们再带入\(w_n^{k+\frac{n}{2}}\)试试

\(f(x)=a((w_n^{k+\frac{n}{2}})^2)+w_n^{k+\frac{n}{2}}b((w_n^{k+\frac{n}{2}})^2)\)

\(f(x)=a(w_n^{2k+n})+w_n^{k+\frac{n}{2}}b(w_n^{2k+n})\)

\(f(x)=a(w_n^{2k})-w_n^{k}b(w_n^{2k})\)

\(f(x)=a(w_{\frac{n}{2}}^{k})-w_n^kb(w_{\frac{n}{2}}^{k})\)

我们求出1的时候就可以顺带求出2来了。

IFFT

一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数.

意思就是说FFT和IFFT可以一起搞.

不明白，留坑

具体

递归版fft好像一班都不写，需要蝴蝶效应，二进制什么的的优化成非递归版。

代码

#include <bits/stdc++.h>

using namespace std;

const int N=4e6+7;

const double Pi=acos(-1.0);

int read() {

	int x=0,f=1;char s=getchar();

	for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;

	for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';

	return x*f;

}

int n,m,r[N],limit=1;

struct Complex {

	double x,y;

	Complex(double xx=0,double yy=0) {x=xx,y=yy;}

}a[N],b[N];

Complex operator + (Complex a,Complex b) {return Complex(a.x+b.x,a.y+b.y);}

Complex operator - (Complex a,Complex b) {return Complex(a.x-b.x,a.y-b.y);}

Complex operator * (Complex a,Complex b) {return Complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

void fft(Complex *a,int type) {

	for(int i=0;i<=limit;++i)

		if(i<r[i]) swap(a[i],a[r[i]]);

	for(int mid=1;mid<limit;mid<<=1) {

		Complex Wn(cos(Pi/mid),type*sin(Pi/mid));

		for(int R=mid<<1,j=0;j<limit;j+=R) {

			Complex w(1,0);

			for(int k=0;k<mid;++k,w=w*Wn) {

				Complex x=a[j+k],y=w*a[j+mid+k];

				a[j+k]=x+y;

				a[j+k+mid]=x-y;

			}

		}

	}

}

int main() {

	n=read(),m=read();

	for(int i=0;i<=n;++i) a[i].x=read();

	for(int i=0;i<=m;++i) b[i].x=read();

	int l=0;while(limit<=n+m) limit<<=1,l++;

	for(int i=0;i<=limit;++i)

		r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));

	fft(a,1),fft(b,1);

	for(int i=0;i<=limit;++i) a[i]=a[i]*b[i];

	fft(a,-1);

	for(int i=0;i<=n+m;++i) printf("%d ",(int)(a[i].x/limit+0.5));

	return 0;

}

参考||引用

鸣谢

zhihu大佬

 路人黑的纸巾

 胡小兔

 attack