2017 ACM/ICPC Asia Regional Shenyang Online number number number

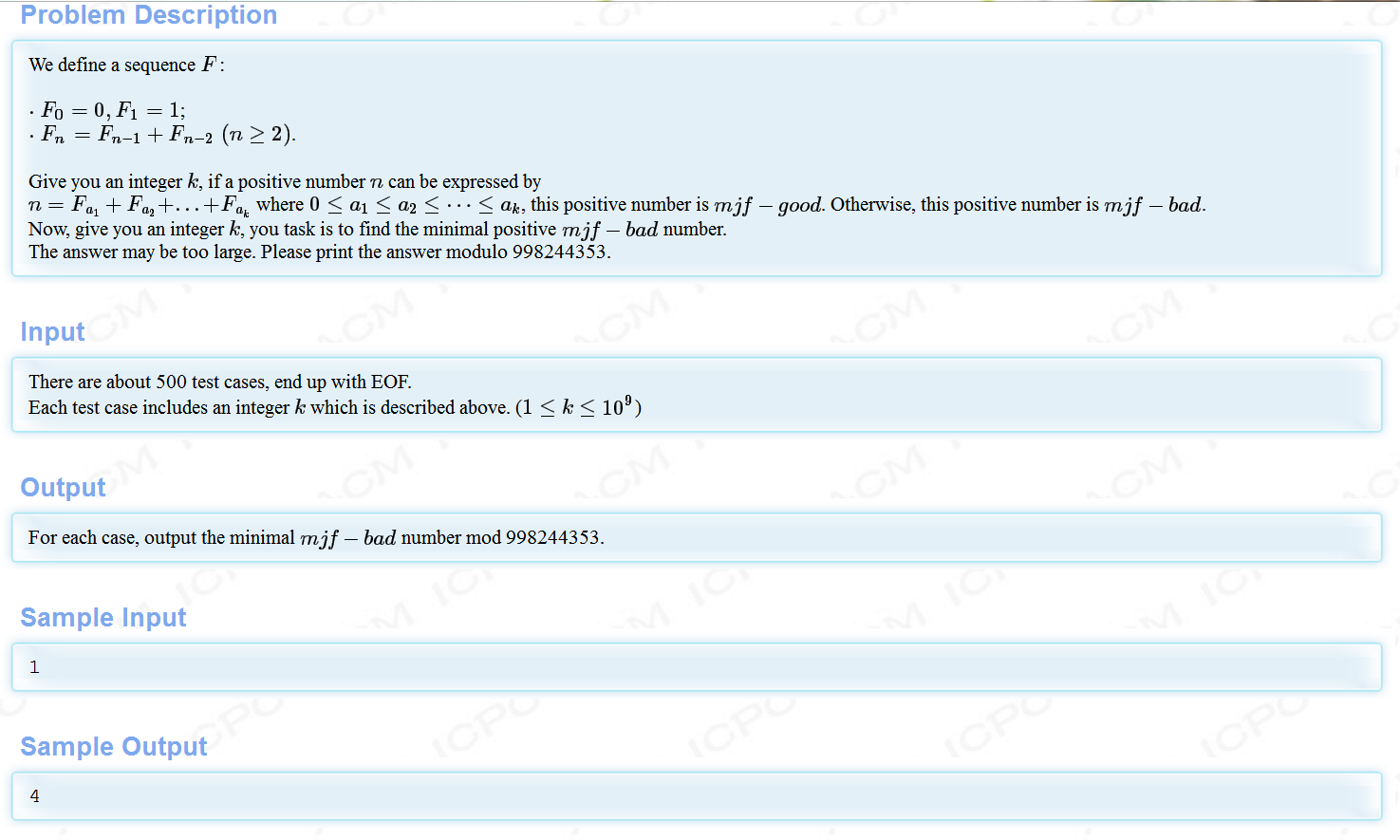
题意：求n个斐波那契数列组合都无法得到的最小数字

解法：

1 我们先暴力的求出前面几个数字

2 然后再暴力的求递推

3 接着矩阵快速幂(没写错吧？)

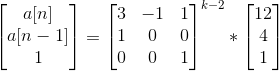
/*#include<bits/stdc++.h>
using namespace std;
long long x[50];
map<long long,int>Mp;
void dfs(int pos,long long sum,int cnt,int n){
    if(cnt==n){
        Mp[sum]=1;
        return;
    }
    if(cnt>n){
        return;
    }
    for(int i=pos;i<=20;i++){
        dfs(i+1,sum+x[i],cnt+1,n);
    }
}
int main(){
    x[0]=0;
    x[1]=1;
    for(int i=2;i<=21;i++){
        x[i]=x[i-1]+x[i-2];
    }
    for(int i=0;i<=21;i++){
        Mp[x[i]]=1;
    }
    //dfs(0,0,0,3);
    for(int i=2;i<=5;i++){

        dfs(0,0,0,i);
        for(long long j=0;j<=x[21];j++){
            if(Mp[j]==0){
                cout<<j<<endl;
                break;
            }
        }
    }
    return 0;
}*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#define mset(a,i) memset(a,i,sizeof(a))
using namespace std;
typedef long long ll;
const int mod=;
struct Mal{
    ll x[][];
};
Mal mul(Mal a,Mal b){
    Mal c;
    memset(c.x,,sizeof(c.x));
    for(int i=;i<;i++){
        for(int j=;j<;j++){
            for(int k=;k<;k++){
                c.x[i][j]+=((a.x[i][k]+mod)*(b.x[k][j]+mod))%mod;
                c.x[i][j]%=mod;
            }
        }
    }
    return c;
}
Mal Qp(int n){
    Mal a,b;
    memset(a.x,,sizeof(a.x));
    memset(b.x,,sizeof(b.x));
    a.x[][]=;
    a.x[][]=-;
    a.x[][]=;
    a.x[][]=;
    a.x[][]=;
    for(int i=;i<;i++){
        b.x[i][i]=;
    }
    while(n){
        if(n&){
            b=mul(b,a);
        }
        a=mul(a,a);
        n/=;
    }
    return b;
}
ll k;
int main(){
    while(~scanf("%lld",&k)){
        if(k==){
            cout<<""<<endl;
            continue;
        }
        if(k==){
            cout<<""<<endl;
            continue;
        }
        Mal pos,X;
        pos.x[][]=;
        pos.x[][]=;
        pos.x[][]=;
        X=mul(Qp(k-),pos);
        ll ans=X.x[][]%mod;
        printf("%lld\n",ans);
    }
    return ;
}
/*
1 2 3 4 5 6 7 8 9 10 11 12
4
12
33
88
232
609
1596
4180
10945
28656
75024
196417
99999999
702476551
9999999
395293026
*/