高斯判别分析模型（ Gaussian discriminant analysis）及Python实现

高斯判别分析模型（ Gaussian discriminant analysis）及Python实现

http://www.cnblogs.com/sumai

1.模型

高斯判别分析模型是一种生成模型，而之前所提到的逻辑回归是一种判别模型，生成模型和判别模型的详细了解可参考这篇文章：

http://blog.sciencenet.cn/home.php?mod=space&uid=248173&do=blog&id=227964

简单的来说，我们的目标都是p(y|x)，判别模型是构造一个函数f(x)去逼近p(y|x)，而对于生成模型则是通过贝叶斯公式p(y|x) = p(x|y)p(y)/p(x)，求得p(x|y)和p(y)来间接得到p(y|x)。

首先，高斯判别分析模型对变量x和y有如下假设：

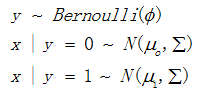
　　    这样，可以给出概率密度函数：

2.评价

该模型的对数似然函数如下：

3.优化

对各个参数进行求导后令等式为0，得到：

　　  Φ是训练样本中结果 y=1 占有的比例。
　　  μ0是 y=0 的样本中特征均值。
　　  μ1是 y=1 的样本中特征均值。
　　  Σ是样本特征方差均值。

4.python代码实现

 # -*- coding: utf-8 -*-
 """
 Created on Tue Mar 08 16:16:36 2016

 @author: SumaiWong
 """

 import numpy as np
 import pandas as pd
 from numpy import dot
 from numpy.linalg import inv

 iris = pd.read_csv('D:\iris.csv')
 dummy = pd.get_dummies(iris['Species']) # 对Species生成哑变量
 iris = pd.concat([iris, dummy], axis =1 )
 iris = iris.iloc[0:100, :] # 截取前一百行样本

 X = iris.ix[:, 0:4]
 Y = iris['setosa'].reshape(len(iris), 1) #整理出X矩阵 和 Y矩阵

 def GDA(Y, X):
     theta1 = Y.mean() #类别1的比例
     theta0 = 1-Y.mean() #类别2的比例
     mu1 = X[Y==1].mean() #类别1特征的均值向量
     mu0 = X[Y==0].mean() #类别2特征的均值向量

     X_1 = X[Y==1]
     X_0 = X[Y==0]
     A = dot(X_1.T, X_1) - len(Y[Y==1])*dot(mu1.reshape(4,1), mu1.reshape(4,1).T)
     B = dot(X_0.T, X_0) - len(Y[Y==0])*dot(mu0.reshape(4,1), mu0.reshape(4,1).T)
     sigma = (A+B)/len(X) #sigma = X'X-n(X.bar)X.bar'=X'[I-1/n 1 1]X  

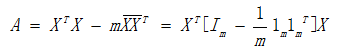
     return theta1, theta0, mu1, mu0, sigma