Levmar:Levenberg-Marquardt非线性最小二乘算法

Abstract. Levmar is GPL native ANSI C implementations of the Levenberg-Marquardt optimization algorithm.The blog focus on the compilation of levmar on Windows with Visual Studio.

Key Words. Levmar, C, LM least squares

1. levmar简介

Gauss-Newton算法是一个古老的处理非线性最小二乘问题的方法。该方法在迭代过程中要求矩阵J(x)满秩。为了克服这个困难，Levenberg(1944)提出了一种新的方法，但未受到重视。后来Marquardt(1963)又重新提出，并在理论上进行了控讨，得到Levenberg-Marquardt方法，简称LM方法。在此基础上，Fletcher(1971)对其实现策略进行了改进，得到了Levenberg-Marquardt-Fletcher方法（LMF）。再后来，More(1978)将LM方法与信赖域方法结合，建立了带信赖域的LM方法。

LM算法的产生主要是解决曲线最小二乘拟合问题，现在很多软件使用LM算法来解决通用的曲线拟合问题。

本文主要介绍GPL开源库levmar2.6使用Visual Studio在Windows上进行编译。这个开源库的官方网站是：http://users.ics.forth.gr/~lourakis/levmar/

2. 编译levmar

下载源码levmar-2.6解压，在其README.txt中对levmar的授权GPL、编译等进行了说明。在Windows操作系统中，可以使用nmake /f Makefile.vc来编译levmar和一个示例程序。

从官网介绍可知，levmar有些算法依赖LAPACK库，一个线性代数计算开源库。所以如果要使用那些算法，编译的时候必须包含这个库。从示例程序的源文件lmdemo.c中可以看出，有些问题的求解是需要LAPACK库的，相关源码列出如下：

  /* uncomment the appropriate line below to select a minimization problem */

  problem=

          //0; // Rosenbrock function

          //1; // modified Rosenbrock problem

          //2; // Powell's function

      //3; // Wood's function

          ; // Meyer's (reformulated) problem

          //5; // Osborne's problem

      //6; // helical valley function

#ifdef HAVE_LAPACK

      //7; // Boggs & Tolle's problem 3

      //8; // Hock - Schittkowski problem 28

      //9; // Hock - Schittkowski problem 48

      //10; // Hock - Schittkowski problem 51

#else // no LAPACK

#ifdef _MSC_VER

#pragma message("LAPACK not available, some test problems cannot be used")

#else

#warning LAPACK not available, some test problems cannot be used

#endif // _MSC_VER

#endif /* HAVE_LAPACK */

      //11; // Hock - Schittkowski problem 01

      //12; // Hock - Schittkowski modified problem 21

      //13; // hatfldb problem

      //14; // hatfldc problem

      //15; // equilibrium combustion problem

#ifdef HAVE_LAPACK

      //16; // Hock - Schittkowski modified #1 problem 52

      //17; // Schittkowski modified problem 235

      //18; // Boggs & Tolle modified problem #7

      //19; // Hock - Schittkowski modified #2 problem 52

      //20; // Hock - Schittkowski modified problem #76"

#endif /* HAVE_LAPACK */

  switch(problem){

  default: fprintf(stderr, "unknown problem specified (#%d)! Note that some minimization problems require LAPACK.\n", problem);

           exit();

    break;

从上述源码可知，如果LAPACK库不可用的时候，示例程序中的问题

l 7 Boggs & Tolle’s problem 3

l 8 Hock - Schittkowski problem 28

l 9 Hock - Schittkowski problem 48

l 10 Hock - Schittkowski problem 51

l 16 Hock - Schittkowskit modified #1 problem 52

l 17 Schittkowski modified problem 235

l 18 Boggs & Tolle modified problem #7

l 19 Hock - Schittkowski modified #2 problem 52

l 20 Hock - Schittkowski modified probem #76

这些问题的求解功能是不能使用的。从头文件levmar.h中要以看出，

#ifdef LM_DBL_PREC

/* double precision LM, with & without Jacobian */

/* unconstrained minimization */

extern int dlevmar_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, int itmax, double *opts,

      double *info, double *work, double *covar, void *adata);

extern int dlevmar_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, int itmax, double *opts,

      double *info, double *work, double *covar, void *adata);

/* box-constrained minimization */

extern int dlevmar_bc_der(

       void (*func)(double *p, double *hx, int m, int n, void *adata),

       void (*jacf)(double *p, double *j, int m, int n, void *adata),

       double *p, double *x, int m, int n, double *lb, double *ub, double *dscl,

       int itmax, double *opts, double *info, double *work, double *covar, void *adata);

extern int dlevmar_bc_dif(

       void (*func)(double *p, double *hx, int m, int n, void *adata),

       double *p, double *x, int m, int n, double *lb, double *ub, double *dscl,

       int itmax, double *opts, double *info, double *work, double *covar, void *adata);

#ifdef HAVE_LAPACK

/* linear equation constrained minimization */

extern int dlevmar_lec_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *A, double *b, int k,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

extern int dlevmar_lec_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *A, double *b, int k,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

/* box & linear equation constrained minimization */

extern int dlevmar_blec_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub, double *A, double *b, int k, double *wghts,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

extern int dlevmar_blec_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub, double *A, double *b, int k, double *wghts,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

/* box, linear equations & inequalities constrained minimization */

extern int dlevmar_bleic_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub,

      double *A, double *b, int k1, double *C, double *d, int k2,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

extern int dlevmar_bleic_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub,

      double *A, double *b, int k1, double *C, double *d, int k2,

      int itmax, double *opts, double *info, double *work, double *covar, void *adata);

/* box & linear inequality constraints */

extern int dlevmar_blic_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

extern int dlevmar_blic_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *lb, double *ub, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

/* linear equation & inequality constraints */

extern int dlevmar_leic_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *A, double *b, int k1, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

extern int dlevmar_leic_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *A, double *b, int k1, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

/* linear inequality constraints */

extern int dlevmar_lic_der(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      void (*jacf)(double *p, double *j, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

extern int dlevmar_lic_dif(

      void (*func)(double *p, double *hx, int m, int n, void *adata),

      double *p, double *x, int m, int n, double *C, double *d, int k2,

      int itmax, double opts[], double info[LM_INFO_SZ], double *work, double *covar, void *adata);

#endif /* HAVE_LAPACK */

#endif /* LM_DBL_PREC */

从头文件levmar.h中的代码可以看出，在#ifdef HAVE_LAPACK和#endif /* HAVE_LAPACK */之间的函数都是不可用的。除此之外的函数是可用的，如基本的dlevmar_der和dlevmar_dif等函数是不依赖LAPACK库的。如果只使用这几个函数，则可以不用配置LAPACK库，编译levmar就很简单了。

如果不使用LAPACK库，可以先在头文件levmar.h中把#define HAVE_LAPACK 这一行注释掉：

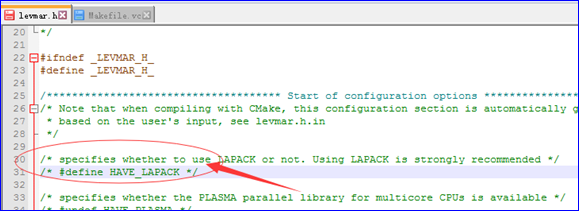
然后再修改Makefile.vc文件，在Makefile.vc中可以看到如下图所示一句注释，即当不使用LAPACK库是，把那一行注释掉（前面加#）：

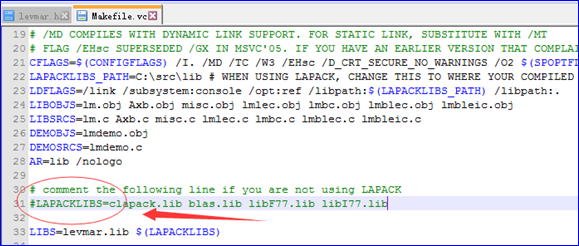
这时就可以启动Visual Studio的编译器CL来编译levmar库了。配置好编译环境的命令工具从Visual Studio的菜单来启动：

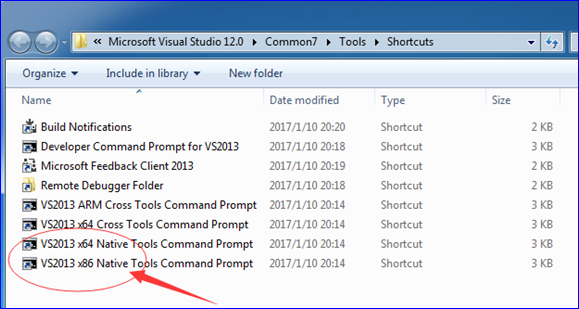
要编译32位的levmar库，可以使用x86的命令工具，要编译64位的levmar，可以使用x64的命令工具。启动命令工具后，切换到levmar源码文件夹，并输入命令

nmake /f Makefile.vc

如下图所示：

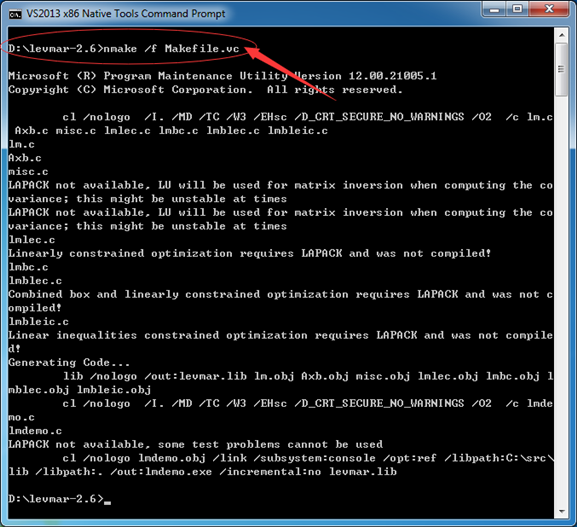
编译成功生成levmar.lib和lmdemo.exe说明编译成功了。

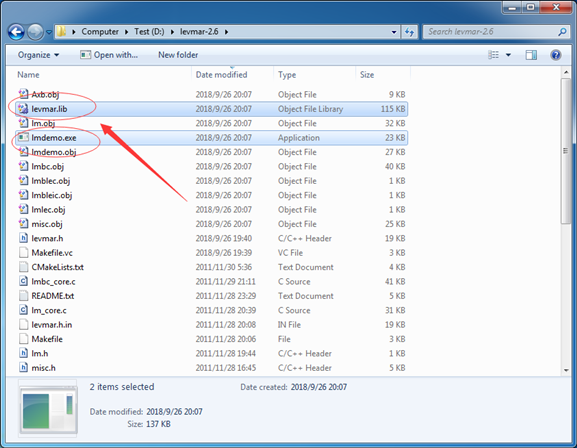
接着在命令窗口中运行lmdemo.exe，测试levmar例子程序。如果lmdemo正常运行，说明levmar已经成功编译。

自己的程序如果要使用levmar，就可以像使用其他开源库一样，设置头文件路径及库levmar.lib的路径，就可以使用了。