HDU 1143 Tri Tiling （递推）

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 2118    Accepted Submission(s): 1211

Problem Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.

 

Output

For each test case, output one integer number giving the number of possible tilings.

 

Sample Input

2
8
12
-1

 

Sample Output

3
153
2131

 

Source

University of Waterloo Local Contest 2005.09.24

 

Recommend

Eddy   |   We have carefully selected several similar problems for you:  1133 1267 1207 1249 1284

转：：：，假设n为奇数，必定无解。

当n为偶数时，一个比較直观的思路就是把大矩形用竖线切出左边一部分，然后递归求解，就像UVA_10359那样，直接考虑最左边一个小矩形是怎样构成的我们就能够递归得到f(n)递推式。

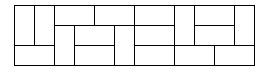
尽管这个题目乍看上去小矩形似乎拼法比較多，并且要拼出一个不能再用竖线切分的小矩形似乎拼的方法也并不直观。但假设我们在纸上多画一画的话，对于拼随意一个横向边长为x的不可再用竖线切分的小矩形，假设x为2，显然有3种拼法，假设x为大于2的偶数，那么仅仅有2种拼法。

至于假设x>2为什么仅仅有两种拼法，我们最好还是实际拼一下。首先第一列肯定仅仅有两种情况，第一种是一个横的在上面，然后一个竖的在左下方，另外一种是一个横的在以下，然后一个竖的在左上方，由于两种情况对称，我们仅仅讨论第一种情况。

如今已经拼好两个了，假设横的以下再放一个竖的，那么显然这个就成了一个x=2的小矩形了，那么最后拼出来的就不符合我们前面说的不可再用竖线切分的特征了，因此横的以下也即竖的右边，仅仅能再放两个横的，放完两个横的我们就发现两个横的上面有一个小正方形区域，这个区域仅仅能楔进去一个横的，等把这个横的画完之后，MyGod，我们会发现一个惊人的事实，如今的这个结构是和我们最初放完一个横的一个竖的的那种情况的结构是一样的！因此，假设我们想继续向右拼出不能被竖线切分的矩形，那么仅仅能是反复之前的操作，因而得到的最后横向边长为x的矩形是唯一确定的。

前面我们最初拼的时候仅仅取了对称的两种情况之中的一个，因此，假设x>2，拼出一个不能被竖线分割的矩形的方法仅仅有两种。

那么递推公式自然就有了，f(n)=3*f(n-2)+2*f(n-4)+…+2*f(0)，然后再写出f(n-2)的递推式后两式作差就能够得到f(n)=4*f(n-2)-f(n-4)，递归的边界是f(0)=1，f(2)=4。

代码：0MS

#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <string.h>
using namespace std;
#define M 31
int f[M]={1,3};
int main()
{
    int i,n;
    for(i=2;i<M;i++) f[i]=4*f[i-1]-f[i-2];
   while(cin>>n)
    {
        if(n<0) break;
        if(n%2==0) cout<<f[n/2]<<endl;
        else cout<<0<<endl;
    }
    return 0;
}