【codeforces 757E】Bash Plays with Functions

【题目链接】:http://codeforces.com/problemset/problem/757/E

【题意】



给你q个询问;

每个询问包含r和n;

让你输出f[r][n];

这里f[0][n]是n分解成两个数u,v的乘积的个数;

这里u和v互质;

而f[r][n]当r>0时,有个递推式;

【题解】



那个递推式等价于



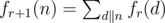
即n的所有因子x的f[r][x]的和;

这里需要知道;

f[0][n]=2n的不同质因子个数

且容易得到

当a和b互质的时候,f[0][a*b]=f[0][a]*f[0][b];

则f[0]是积性函数;

有个定理就是;

如果是类似上面那个递推

如果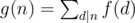且f为积性函数,则g也为积性函数;

则我们在算

f[r][n]的时候可以对n分解质因数;

即f[r][p1^q1*p2^q2…pm^qm];

这样p1^q1..p2^q2..pm^qm都是互质的了;

则可以利用积性函数把它们分解成

f[r][p1^q1]*f[r][p2^q2]..*f[r][pm^qm];

这里

f[0][p^q]的值除了q=0的时候为1之外,其他情况都为2,因为p是质数,可知不同的质因子个数只有1个,也即这个质数p;所以都是2^1;

q为0的时候,只有1,1这种情况,所以只有一对;为1;

(所以这里的p只要为质数,是几都无所谓,f[0]的值都一样)

而

根据

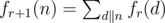可知

f[r+1][pq]=∑f[r][p0..q]⋅⋅⋅①

因为p0..q都是pq的因子

这样其实就能看出来了,要算f[r][p^q]的时候,根本不需要知道p是多少;

f[r][p^q]只与q和r有关;

根据①式能够很容易写个dp;

具体的

g[0][0] = 1,g[0][1..n] = 2;

g[i][0] = g[i-1][0];

g[i][j]=∑g[i−1][0..j]

对于要算的

f[r][p1q1]∗f[r][p2q2]..∗f[r][pmqm];

直接输出

g[r][q1]∗g[r][q2]∗...∗g[r][qm]

就好;

在对n分解质因数的时候,好像用到了更牛逼的方式.

类似筛法的东西吧.

快速获取某个值的质因子;

(用cin竟然会超时…再也不用了!…还是算了吧,cin还是比较方便的,记住可能会因为这个超时就好…)



【Number Of WA】



5



【完整代码】

#include <bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define ms(x,y) memset(x,y,sizeof x)
#define Open() freopen("F:\\rush.txt","r",stdin)
#define Close() ios::sync_with_stdio(0),cin.tie(0)

typedef pair<int,int> pii;
typedef pair<LL,LL> pll;

const int dx[9] = {0,1,-1,0,0,-1,-1,1,1};
const int dy[9] = {0,0,0,-1,1,-1,1,-1,1};
const double pi = acos(-1.0);
const int N = 1e6;
const int MOD = 1e9+7;

int dp[N+100][21],lp[N+10];

void pre()
{
    lp[1] = 1;
    rep1(i,2,N)
        if (lp[i]==0)
            for (int j = i;j<=N;j+=i)
                lp[j] = i;

    rep1(i,1,20)
        dp[0][i] = 2;
    rep1(i,0,N)
        dp[i][0] = 1;
    rep1(i,1,N)
        rep1(j,1,20)
            dp[i][j] = (dp[i][j-1] + dp[i-1][j])%MOD;
}

int main()
{
    //Open();
    pre();
    int q;
    scanf("%d",&q);
    while (q--)
    {
        int r,n;
        scanf("%d%d",&r,&n);
        LL ans = 1;
        while (n>1)
        {
            int cnt = 0,x = lp[n];
            while (n%x==0)
            {
                cnt++;
                n/=x;
            }
            ans = (ans*dp[r][cnt])%MOD;
        }
        printf("%lld\n",ans);
    }
    return 0;
}