Newton法（牛顿法 Newton Method）

           1、牛顿法应用范围

                         牛顿法主要有两个应用方向：1、目标函数最优化求解。例：已知 f(x)的表达形式，，求 ，及g(x)取最小值时的 x ?，即

                                                          由于||f(x)||通常为误差的二范数，此时这个模型也称为最小二乘模型，即。

                                                      2、方程的求解（根）。例：求方程的解：g(x) = 0，求 x ？

                    这两个应用方面都主要是针对g(x)为非线性函数的情况。2中，如果g(x)为线性情况下的求解通常使用最小二乘法求解。

                         牛顿法的核心思想是对函数进行泰勒展开。

           2、牛顿法用于方程求解

                    对f(x)进行一阶泰勒公式展开：

                                                

                    此时，将非线性方程 g(x) = 0 近似为线性方程：

                                                

                    若 f’(x) != 0，则下一次迭代解为：

                                                   

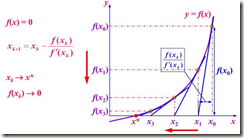
                    牛顿迭代示意图（因此Newton迭代法也称为切线法）：

                                         

          3、牛顿法用于函数最优化求解

                     对f(x)进行二阶泰勒公式展开：

                                               

                     此时，将非线性优化问题 min f(x) 近似为为二次函数的最优化求解问题：

                                               

                     对于（5）式的求解，即二次函数（抛物线函数）求最小值，对（5）式中的函数求导：

                                               

                                              

                     从本质上来讲，最优化求解问题的迭代形式都是： ，

                     其中k为系数，为函数的梯度（即函数值上升的方向），那么为下降的方向，

                     最优化问题的标准形式是：求目标函数最小值，只要每次迭代沿着下降的方向迭代那么将逐渐达到最优，

                     而牛顿将每次迭代的步长定为：。

            4、补充

                          a、严格来讲，在“3、牛顿法用于函数最优化求解”中对函数二阶泰勒公式展开求最优值的方法称为：Newton法，

                         而在“2、牛顿法用于方程求解”中对函数一阶泰勒展开求零点的方法称为：Guass-Newton（高斯牛顿）法。

                     b、在上面的陈述中，如果x是一个向量，那么公式中：

                         应该写成：，为Jacobi(雅克比)矩阵。

                         应该写成：，为Hessian（海森）矩阵。

                     c、牛顿法的优点是收敛速度快，缺点是在用牛顿法进行最优化求解的时候需要求解Hessian矩阵。

                         因此，如果在目标函数的梯度和Hessian矩阵比较好求的时候应使用Newton法。

                         牛顿法在进行编程实现的时候有可能会失败，具体原因及解决方法见《最优化方法》-张薇 东北大学出版社 第155页。

           5、Newton法与Guass-Newton法之间的联系

                        对于优化问题 ，即，当理论最优值为0时候，这个优化问题就变为了函数求解问题：

                                                             

                          结论：当最优化问题的理论最小值为0时，Newton法求解就可变为Guass-Newton法求解。        

                     另外：对f(x)进行二阶泰勒展开：

                                                            

                          f(x)乘以f(x)的转置并忽略二次以上的项：

                                  

                                                     

                                                   

                                                   

                     因此，当在最优解附近时，即满足，此时可认为：

            6、扩展阅读

                        a、修正牛顿(Newton)法

                    b、共轭方向法与共轭梯度法

                    c、拟牛顿法（避免求解Hessian矩阵）：DFP算法、BFGS算法

            自己所有博客汇总