[2019HDU多校第二场][HDU 6591][A. Another Chess Problem]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6591

题目大意：二维坐标系上，所有满足\(5|2x+y\)的点都被设为障碍物，无法通过。现给出一对点，问从其中一点走到另一点的最少移动次数以及对应的方案数（每次可以移动一个单位长度）

题解：首先把图画出来，是长这样的

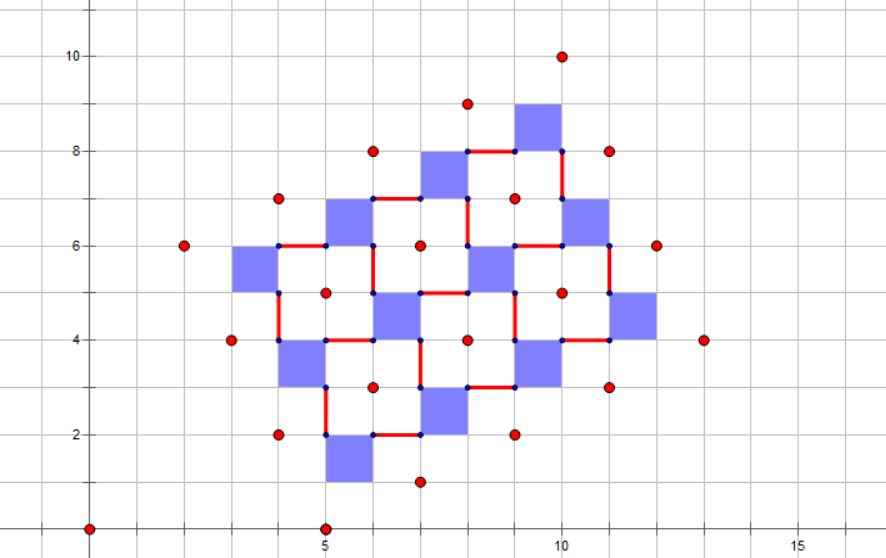
　　　图中所有不能被走过的点用红点表示。可以发现（这个是五子棋中的八卦阵）这些点将图中的格点分成了若干个小块（图中用蓝色方块标出），每个小块里四个点保证两两之间的距离不会被红点所影响。于是我们可以考虑将点与所在的块对应起来，将点之间的移动转换为块之间的移动计算答案。

　　　本人在这题中是将每个方块下方的红点作为该块对应的点，并以点\((2,1)\)当做新坐标系下的\((1,0)\)来进行坐标系的转化，而在块中，可以设每个方块的左上角为点\(0\)，顺时针依次设为\(1,2,3\)，这样方便之后计算在同一块内进行移动的答案。

　　　转换完坐标系后，对于块间的移动，就可以看成求我要移动\(n\)行，\(m\)列的方案数。这里由于\(n,m\)可能为负数，于是可以考虑将他们全部转换为正数之后再做，转换的方法有很多，其中一种方法是：先判断\(n\)的正负，如果为负可以交换起点和终点，这样答案是一样的，之后判断\(m\)的正负，如果为负则可以做一个对称变换，将\(m\)改为正数，这里要注意点在块内的位置也可能会发生改变。

　　　然后我们会发现，如果我们连续往一个方向移动，移动的步数会比交错方向要多，因此我们要尽量减少连续往相同方向移动的次数，这个最少的次数是可以计算出来的，假设其为\(t\)，那么方案数就要乘上\(2^t\)，这是因为连续往一个方向走的时候，必须要在块内走对角线，因此每次会有两种走法。另外我们还要考虑在不同位置改变移动方向的方案数，这个是可以用组合数来计算的，之后我们就只需要枚举从起点块的哪一点出发以及到达终点块时处于哪一个点即可。

#include<bits/stdc++.h>
using namespace std;
#define N 200001
#define LL long long
#define MOD 998244353
int T,n,m,ans,num,f[N],p[N],q[N],dis[][];
struct Point
{
    int x,y,o;
    void read(){scanf("%d%d",&x,&y);}
    void get()
      {
      int tmp=((*x+y)%+)%;
      if(tmp==)o=,y-=;
      else if(tmp==)o=,x--,y-=;
      else if(tmp==)o=,x--,y--;
      else if(tmp==)o=,y--;
      else while(true);
      int tmpx=(*x+y)/,tmpy=(*y-x)/;
      x=tmpx,y=tmpy;
      }
}A,B;
void pretype()
{
    f[]=;
    p[]=q[]=;
    f[]=p[]=q[]=;
    for(int i=;i<N;i++)
      {
      f[i]=2ll*f[i-]%MOD;
      p[i]=1ll*p[i-]*i%MOD;
      q[i]=1ll*(MOD-MOD/i)*q[MOD%i]%MOD;
      }
    for(int i=;i<N;i++)
      q[i]=1ll*q[i-]*q[i]%MOD;
    for(int i=;i<;i++)
      for(int j=;j<;j++)
        dis[i][j]=min(abs(i-j),-abs(i-j));
}
int C(int n,int m){return 1ll*p[n]*q[m]%MOD*q[n-m]%MOD;}
void rua(int o1,int o2,int n,int m)
{
    int w[]={n,m};
    int res=,tot=,t;
    if(w[o1]< || w[o2]<)return;
    if(o1==o2 && w[o1]< && n+m>)return;
    res=(n+m)*-;
    if(n+m>)
      {
      w[o1]--,w[o2]--;
      if(o1==o2)
        {
        t=abs(w[o1]+-w[o1^]);
        res+=t,tot=f[t];
        if(w[o1]+>=w[o1^])
          tot=1ll*tot*C(w[o1]+,w[o1^])%MOD;
        else tot=1ll*tot*C(w[o1^]-,w[o1])%MOD;
        }
      else
        {
        t=abs(w[o1]-w[o2]);
        res+=t,tot=f[t];
        if(w[o1]>=w[o2])
          tot=1ll*tot*C(w[o1],w[o2])%MOD;
        else tot=1ll*tot*C(w[o2],w[o1])%MOD;
        }
      }
    t=dis[o1][A.o];
    res+=t;if(t>)tot=2ll*tot%MOD;
    t=dis[o2+][B.o];
    res+=t;if(t>)tot=2ll*tot%MOD;
    if(res==ans)num=(num+tot)%MOD;
    if(res<ans)ans=res,num=tot;
}
int main()
{
    pretype();
    scanf("%d",&T);
    while(T--)
      {
      A.read(),A.get();
      B.read(),B.get();
      n=B.y-A.y,m=B.x-A.x;
      if(n== && m==)
        {
        ans=dis[A.o][B.o];
        num=ans>?:;
        printf("%d %d\n",ans,num);
        continue;
        }
      if(n< || (n== && m<))
        swap(A,B),n=-n,m=-m;
      if(m<)A.o=(-A.o)%,B.o=(-B.o)%,m=-m;
      ans=,num=;
      for(int i=;i<;i++)
        for(int j=;j<;j++)
          rua(i,j-,n,m);
      printf("%d %d\n",ans,num);
      }
}