DP&图论 DAY 7 上午

DP&图论  DAY 7  上午

图论练习题

P2176 [USACO14FEB]路障Roadblock

先跑最短路（最多n条边，否则出环）

枚举每条边，加倍，再跑 dijkstra

取最大

P2939 [USACO09FEB]改造路Revamping Trails

Solution

分层图最短路

从上一层到下一层，起点之间连边

Solution

暴力N^2建边

然后发现有一些边是没用的

假设存在3个点  （x1,y1）   （x2,y2）    （x3,y3）

min( |x1-x3| , |y1-y3| ) = x3-x1
   --->min( |x1-x2| , |y1-y2| ) + min( |x2-x3| , |y2-y3| )

所以如果存在一条路径，st. point1--->point3  =  point1-->point2 + point2-->point3

所以就把路径换成 1--2+2-->3 ，这样一定不会差

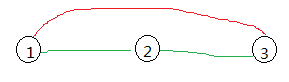
对于所有点，x从小到大排序，y从小到大排序，相邻两点之间连边，不允许跳点的跑路

跑最短路

P2502 [HAOI2006]旅行

Solution

。最小边越大，最大边也越大，不能满足二分性质

。枚举最小边，固定最小边，最小化最大边，最小生成树 kruscal

一开始 sort 一遍

枚举每个最小边，O(M) 克鲁斯卡尔

Solution

最近距离最远，可以二分

N^2连边

二分 mid ，边<mid，属于同一部落内部，看此时图中有多少连通块

数量<k，不可行，数量>=k，继续二分

MST

N^2连边

选若干条边，使得形成 K 个连通块，没选的边中最小值最大

只剩k个连通块，也就是剩下n-k条边，停止算法

kruscal

· Kruskal 最大生成树，加入 N − ne e d 条边就停止。

Solution

S表示前缀和，%2下

可以推理出S1~Sn

S0=0

S[R]----S[L-1]

传递性  x-->y  y-->z ，x-->z

使得每个点都和0连通

加边，跑最小生成树

PS：奇偶异或，连通即可知

MST（最小生成树）

Solution

开到一个不是加油站的点，下一步最优去最近的加油站

以每个加油站为源点，跑多源多汇最短路

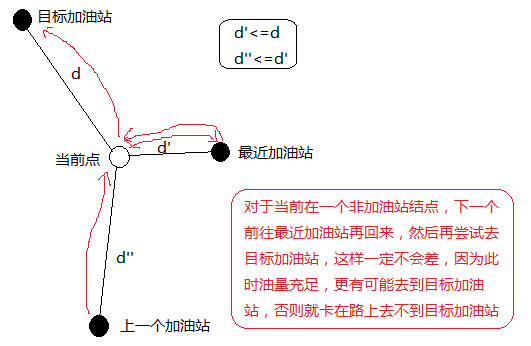
加油站转移

重构边，图上只留下加油站，忽略非加油站点，边权相应更改

也就是

 枚举原图的边，如果两点最近加油站不同，就连边，把最近加油站连边

也就是说：

Solution

Solution

迷一般的好题：file:///C:/Users/Administrator/Documents/Tencent%20Files/1296817027/FileRecv/Contention%20-%20Kick%20Start.htm

真·不是二分

---

下面是不知道在讲啥子系列

线性基

Floyd + 倍增

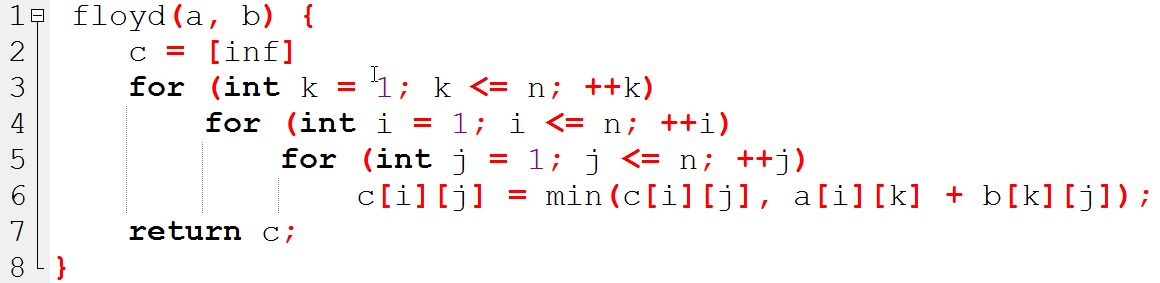
接起来

快速幂加速