Binary Search-使用二叉搜索树

终于到二叉树了，每次面试时最担心面试官问题这块的算法问题，所以接下来就要好好攻克它~

关于二叉树的定义网上一大堆，这篇做为二叉树的开端，先了解一下基本概念，直接从网上抄袭：

先了解下树的概念,balabala~~：

更通俗的定义：

而二叉树就是树结构的一个经典树，也是要讨论的主题，下面再来看下二叉树的定义：

而用二叉树主要是用来干嘛呢？上次不是学习过了一个利用递归实现折半查找的算法（http://www.cnblogs.com/webor2006/p/7182756.html）么？而当时实现的前提是数列一定得有序，那如果数列是无序的，但是也想对它进行搜索，那就可以给它创建一个结构：二叉搜索树，它是二叉树的一种，那它的具体定义是怎么样的？

这里从两个围度来理解：

1、如何构建一个二叉搜索树？

给出一组元素：【5、8、3、4、1、7、6】，构建过程如下：

第一步：将第一个元素【5】做为根结点：

第二步：把第二个元素【8】拿出来与第一个元素做比较，如果比根节点大就放在右边，如果比根节点小就放在左边，由于8>5，则放在5的右边，如下：

第三步：同样的道理 拿出来第三个元素【3】再与根节点进行比较，结果如下：

第四步：上一步已经把二叉树的第二层填满了，接下来的元素【4】首先要与根节点进行比较，再与子树的节点进行比较，如下：

第五步：按照以上的方式，把接下来的元素依次插入到树中即可，下面是剩下元素的整个构建过程：

2、如何从二叉搜索树中查找一个元素？

比如搜“7”这个元素：

1、拿7跟根结点5比，比它大，则搜5的右节点，左节点抛弃；

2、拿7跟8比，比它小，所以必然是在8的左子孙里面，刚好就搜到了。

比如搜“2”这个元素：

1、拿2跟根结点5比，比它小，则搜5的左节点，右节点抛弃；

2、拿2跟3比，比它小，则搜3的左节点，右节点抛弃；

3、拿2跟1比，比它大，则需要转到1的右子孙里找，但是1没有右子孙所以2没有在这个树中，也就是未找到。

有了上面的思路之后，下面来看下具体代码实现，为了方便这里采用JAVA实现：

第一步：构建一个二叉搜索树：

public class BinarySearchTree {
    TreeNode root = null;

    class TreeNode{
      int value;
      int position;
      TreeNode left = null, right = null;
      TreeNode(int value, int position){
        this.value = value;
        this.position = position;
      }
    }

    public void add(int value, int position){
      if(root == null){//生成一个根结点
        root = new TreeNode(value, position);
      } else {
        //生成叶子结点
        add(value, position, root);
      }
    }

    private void add(int value, int position, TreeNode node){
      if(node == null)
        throw new RuntimeException("treenode cannot be null");
      if(node.value == value)
        return; //ignore the duplicated value
      if(value < node.value){
        if(node.left == null){
          node.left = new TreeNode(value, position);
        }else{
          add(value, position, node.left);
        }
      }else{
        if(node.right == null){
          node.right = new TreeNode(value, position);
        }else{
          add(value, position, node.right);
        }
      }
    }

    //打印构建的二叉搜索树
    static void printTreeNode(TreeNode node) {
      if(node == null)
        return;
      System.out.println("node:" + node.value);
      if(node.left != null) {
        printTreeNode(node.left);
      }
      if(node.right != null) {
        printTreeNode(node.right);
      }
    }

    public static void main(String[] args) {
      BinarySearchTree bst = new BinarySearchTree();
      int a[] = { 5, 8, 3, 4, 1, 7, 6};
      for(int i = 0; i < a.length; i++){
        bst.add(a[i], i);
      }

      printTreeNode(bst.root);
    }

}

编译运行：

刚好跟之前分析结果一样：

下面分析下具体构造流程：

Loop1: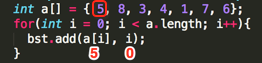

其第一个add(int value, int position)的参数为：value=5、position=0；

　①、，判断root结点是否为null，条件为真，执行循环体：root = TreeNode(5, 0);

#######################################################################

Loop2: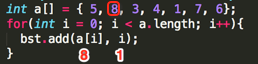

其第一个add(int value, int position)的参数为：value=8、position=1；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、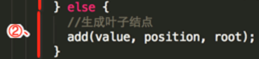,调用第二个add(int value, int position, TreeNode node)方法：add(8, 1, root=TreeNode(5, 0))；

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，8 < 5 为假，继续⑥

　　　　⑥、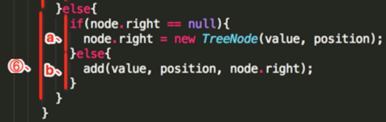

　　　　　　a、判断右接点是否为空，条件为真，于是乎直接生成右接点：node.right = TreeNode(8, 1)
所以此时的二叉树结果如下：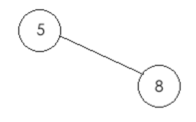

#######################################################################

Loop3:

其第一个add(int value, int position)的参数为：value=3、position=2；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、,调用第二个add(int value, int position, TreeNode node)方法：add(3, 2, root=TreeNode(5, 0))；

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，3 < 5 为真，执行条件体：

　　　　　　a、判断左接点是否为空，条件为真，于是乎直接生成左接点：node.left = TreeNode(3, 2)

所以此时的二叉树结果如下：

#######################################################################

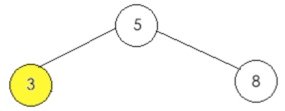
Loop4:

其第一个add(int value, int position)的参数为：value=4、position=3；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、,调用第二个add(int value, int position, TreeNode node)方法：add(4, 3, root=TreeNode(5, 0))；　

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，4 < 5 为真，执行条件体：

　　　　　　a、判断左接点是否为空，条件为假，执行b；

　　　　　　b、add(4, 3, node.left=(3, 2));继续递归：

　　　　　　　　b③、，其条件为假，继续执行④；

　　　　　　　　b④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　　　　　b⑤、，判断要插入的值是否比指定的结点小，4 < 3 为假，继续执行⑥；

　　　　　　　　b⑥、

　　　　　　　　　　a、判断右接点是否为空，条件为真，于是乎直接生成右接点：node.right = TreeNode(4, 3)

所以此时的二叉树结果如下：

#######################################################################

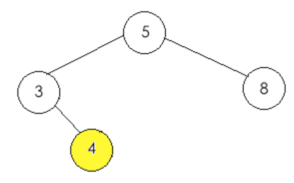
Loop5: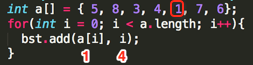

其第一个add(int value, int position)的参数为：value=1、position=4；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、,调用第二个add(int value, int position, TreeNode node)方法：add(1, 4, root=TreeNode(5, 0))；　

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，1 < 5 为真，执行条件体：

　　　　　　a、判断左接点是否为空，条件为假，执行b；

　　　　　　b、add(1, 5, node.left=(3, 2));继续递归：

　　　　　　　　b③、，其条件为假，继续执行④；

　　　　　　　　b④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　　　　　b⑤、，判断要插入的值是否比指定的结点小，1 < 3 为真，执行循环体；

　　　　　　　　　　a、判断左接点是否为空，条件为真，于是乎直接生成左接点：node.left = TreeNode(1, 4)

所以此时的二叉树结果如下：

#######################################################################

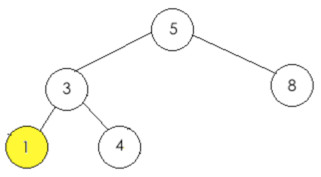
Loop6: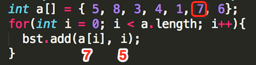

其第一个add(int value, int position)的参数为：value=7、position=5；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、,调用第二个add(int value, int position, TreeNode node)方法：add(7, 5, root=TreeNode(5, 0))；　

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，7 < 5 为假，继续执行⑥：

　　　　⑥、

　　　　　　a、判断右接点是否为空，条件为假，于是执行b;

　　　　　　b、add(7, 5, node.right=(8, 1));继续递归：

　　　　　　　　b③、，其条件为假，继续执行④；

　　　　　　　　b④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　　　　　b⑤、，判断要插入的值是否比指定的结点小，7 < 8 为真，执行循环体；

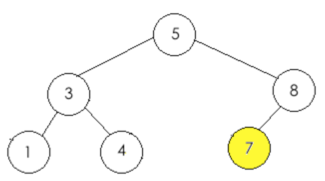
　　　　　　　　　　a、判断左接点是否为空，条件为真，于是乎直接生成左接点：node.left = TreeNode(7, 5)

所以此时的二叉树结果如下：

#######################################################################

Loop7: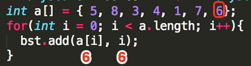

其第一个add(int value, int position)的参数为：value=6、position=6；

　　①、，判断root结点是否为null，条件为假，执行②；

　　②、,调用第二个add(int value, int position, TreeNode node)方法：add(6, 6, root=TreeNode(5, 0))；　

　　　　③、，其条件为假，继续执行④；

　　　　④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　⑤、，判断要插入的值是否比指定的结点小，6 < 5 为假，继续执行⑥：

　　　　⑥、

　　　　　　a、判断右接点是否为空，条件为假，于是执行b;

　　　　　　b、add(6, 6, node.right=(8, 1));继续递归：

　　　　　　　　b③、，其条件为假，继续执行④；

　　　　　　　　b④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　　　　　b⑤、，判断要插入的值是否比指定的结点小，6 < 8 为真，执行循环体；
　　　　　　　　　　a、判断左接点是否为空，条件为假，继续执行b;

　　　　　　　　　　b、add(6, 6, node.right=(7, 5));继续递归：

　　　　　　　　　　　　bb③、，其条件为假，继续执行④；

　　　　　　　　　　　　bb④、,其中要添加的元素在二叉树中木有重复，也就是得保证二叉树中不可能有相同的元素条件为假，继续⑤；

　　　　　　　　　　　　bb⑤、，判断要插入的值是否比指定的结点小，6 < 7 为真，执行循环体；

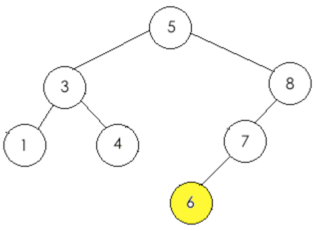
　　　　　　　　　　　　　　　　a、判断左接点是否为空，条件为真，于是乎直接生成左接点：node.left = TreeNode(6, 6)

所以此时的二叉树结果如下：

#######################################################################

于此二叉搜索树就已经完成了~~上面过程有点繁锁，重在体会！！！

第二步：从二叉树中进行数查找：

public class BinarySearchTree {
    TreeNode root = null;

    class TreeNode{
      int value;
      int position;
      TreeNode left = null, right = null;
      TreeNode(int value, int position){
        this.value = value;
        this.position = position;
      }
    }

    public void add(int value, int position){
      if(root == null){//生成一个根结点
        root = new TreeNode(value, position);
      } else {
        //生成叶子结点
        add(value, position, root);
      }
    }

    private void add(int value, int position, TreeNode node){
      if(node == null)
        throw new RuntimeException("treenode cannot be null");
      if(node.value == value)
        return; //ignore the duplicated value
      if(value < node.value){
        if(node.left == null){
          node.left = new TreeNode(value, position);
        }else{
          add(value, position, node.left);
        }
      }else{
        if(node.right == null){
          node.right = new TreeNode(value, position);
        }else{
          add(value, position, node.right);
        }
      }
    }

    //打印构建的二叉搜索树
    static void printTreeNode(TreeNode node) {
      if(node == null)
        return;
      System.out.println("node:" + node.value);
      if(node.left != null) {
        printTreeNode(node.left);
      }
      if(node.right != null) {
        printTreeNode(node.right);
      }
    }

    //搜索结点
    public int search(int value){
      return search(value, root);
    }

    private int search(int value, TreeNode node){
      if(node == null)
        return -1; //not found
      else if(value < node.value){
        System.out.println("Searching left");
        return search(value, node.left);
      }
      else if(value > node.value){
        System.out.println("Searching right");
        return search(value, node.right);
      }
      else
        return node.position;
    }

    public static void main(String[] args) {
      BinarySearchTree bst = new BinarySearchTree();
      int a[] = { 5, 8, 3, 4, 1, 7, 6};
      for(int i = 0; i < a.length; i++){
        bst.add(a[i], i);
      }

      // printTreeNode(bst.root);

      System.out.println(bst.search(8));
      System.out.println(bst.search(3));
      System.out.println(bst.search(6));
      System.out.println(bst.search(30));
    }

}

编译运行：

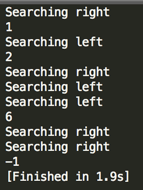
从上面运行结果中，拿搜6来说，只经过了三部：右、左、左，就从无序的数组中找到了，可见其效率是非常高的，最后会对其复杂度进行分析的，下面先来分析一下整个查找的过程：

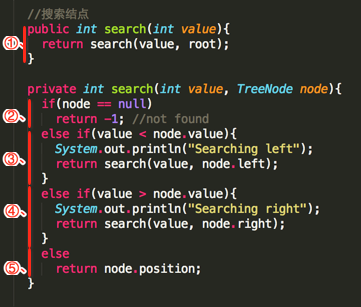
这里就以经过最多步找到“6”为例进行分析吧，

①、search(6, root=TreeNode(5, 0))

②、,其条件不满足，继续执行③；

③、,6 < 5条件为假，执行④;

④、，6 > 5条件为真，执行条件体：
　　打印一下“Searching right”；然后search(6, node.right=TreeNode(8, 0))继续递归：
　　

　　④②、,其条件不满足，继续执行③；

　　④③、,6 < 8条件为真，执行条件体：
　　打印一下“Searching left”；然后search(6, node.left=TreeNode(7, 5))继续递归：
　　

　　　　④③②、,其条件不满足，继续执行③；

　　　　④③③、,6 < 7条件为真，执行条件体：

　　　　　　打印一下“Searching left”；然后search(6, node.left=TreeNode(6, 6))继续递归：

　　　　　　　　④③③②、,其条件不满足，继续执行③；

　　　　　　　　④③③③、,6 < 6条件为假，继续执行④：

　　　　　　　　④、，6 > 6条件为假，继续执行⑤：

　　　　　　　　⑤、，搜索到了结果直接返回，整个递归结束。

时间复杂度分析：

如果写一个循环，从前匹配到尾，那时间复杂度是O(n)，但是使用二叉树来搜索，它的复杂度肯定是小于n的，是跟树的深度有关的，每次递归一次树则向下走一层，那这个二叉搜索树的时间复杂度重点就是看一下树的深度是多少了，是多少呢？log ^ n ，所以说二叉搜索树查找的时间复杂度是O(log ^ n);