【HDU 3590】 PP and QQ （博弈-Anti-SG游戏，SJ定理，树上删边游戏）

PP and QQ

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
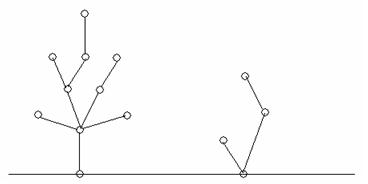
Total Submission(s): 510    Accepted Submission(s): 256

Problem Description

PP and QQ were playing games at Christmas Eve. They drew some Christmas trees on a paper:

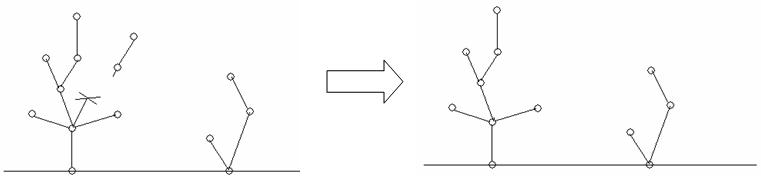
Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows:

PP always moved first. 
PP and QQ took turns (PP was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move won the game. 
Your job is to decide who will finally win the game if both of them use the best strategy. 

Input

The input file contains multiply test cases.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root. 

Output

For each test case, output the name of the winner.

Sample Input

2
2
1 2
2
1 2
1
2
1 2

Sample Output

PP
QQ

Author

alpc27

 

 

【分析】

　　首先是一个树上删边游戏。

　　就是子树的sg+1的乘积啦。。不说了

　　然后是Anti-SG游戏，有SJ定理，具体看jzh的论文吧。

　　

　　证明的话，只需说明：

　　最后的状态符合这个定理。

　　必胜态一定能到一个必败态。

　　必败态到的都是必胜态 即可、

　　这个自己YY瞎搞一下就能证明了。

 

　　就是这样了。

 

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 110

 struct node
 {
     int x,y,next;
 }t[Maxn*];
 int first[Maxn],len;

 void ins(int x,int y)
 {
     t[++len].x=x;t[len].y=y;
     t[len].next=first[x];first[x]=len;
 }

 int dfs(int x,int f)
 {
     int ans=;
     for(int i=first[x];i;i=t[i].next) if(t[i].y!=f)
     {
         ans^=(dfs(t[i].y,t[i].x)+);
     }
     return ans;
 }

 int main()
 {
     int T;
     while(scanf("%d",&T)!=EOF)
     {
         int ans=;
         bool ok=;
         while(T--)
         {
             int n;
             scanf("%d",&n);
             len=;
             for(int i=;i<=n;i++) first[i]=;
             for(int i=;i<n;i++)
             {
                 int x,y;
                 scanf("%d%d",&x,&y);
                 ins(x,y);ins(y,x);
             }
             int nw=dfs(,);
             if(nw>) ok=;ans^=nw;
         }
         if((!ans&&!ok)||(ans&&ok)) printf("PP\n");
         else printf("QQ\n");
     }
     return ;
 }

2017-04-27 17:11:55