Andrew Ng机器学习课程,第一周作业,python版本
Liner Regression
1.梯度下降算法
Cost Function
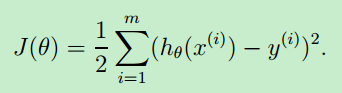
对其求导:

theta更新函数:

代码如下:
from numpy import *
import numpy as np
import matplotlib.pyplot as plt def loadDataSet(filename):
data = []
label = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split(',')
a = [1.0]
a.append(float(curLine[0]))
data.append(a)
label.append([float(curLine[1])])
return data, label def computeCost(X, Y, theta):
theta = mat(theta)
m = shape(X)[0]
J = 1 / (2 * m) * sum(array((X * theta - Y))**2)
return J #矩阵形式的梯度下降算法
def gradientDescentMatrix(X, y, theta, alpha, iterations):
m = shape(y)[0]
theta_s = theta.copy()
for i in range(iterations):
theta = theta - alpha/m * (X.T *(X * theta - y))
return theta #梯度下降算法
def gradientDescent(X, y, theta, alpha, iterations):
m = len(y)
# theta_s = theta :此表达式中共享内存空间
theta_s = theta.copy()
for i in range(iterations):
theta[0] = theta[0] - (alpha/m) * np.sum(np.mat(X)*np.mat(theta_s) - np.mat(y))
p1 = np.mat(X)*np.mat(theta_s) - np.mat(y)
p2 = X[:, 1]*p1
# print(p2)
theta[1] = theta[1] - (alpha / m) * p2
# print(theta[1])
theta_s = theta.copy()
return theta def Plotting(x, y, theta):
f2 = plt.figure(2)
p1 = plt.scatter(x, y, marker='x', color='r', label='Training Data', s=30) x1 = np.linspace(0, 25, 30)
y1 = theta[0] + theta[1] * x1 plt.plot(x1, y1, label="Test Data", color='b') plt.legend(loc='upper right')
plt.show() dataSet, label = loadDataSet("ex1data1.txt")
theta = zeros((2, 1))
iterations = 1500
alpha = 0.01 #数组格式X, Y
X = array(dataSet)
Y = array(label) #矩阵格式 XMat, YMat
XMat = mat(X)
YMat = mat(Y) if 1: #梯度下降算法
theta = gradientDescent(X, Y, theta, alpha, iterations)
else: #矩阵形式的梯度下降算法
theta = gradientDescentMatrix(XMat, YMat, mat(theta), alpha, iterations)
print(theta) x = []
for k in dataSet:
x.append([k[1]])
Plotting(array(x), Y, theta)
代码中对于梯度下降算法有两种形式,一种就是一般形式 gradientDescent(),另一种就是矩阵形式gradientDescentMatrix()
运行效果:
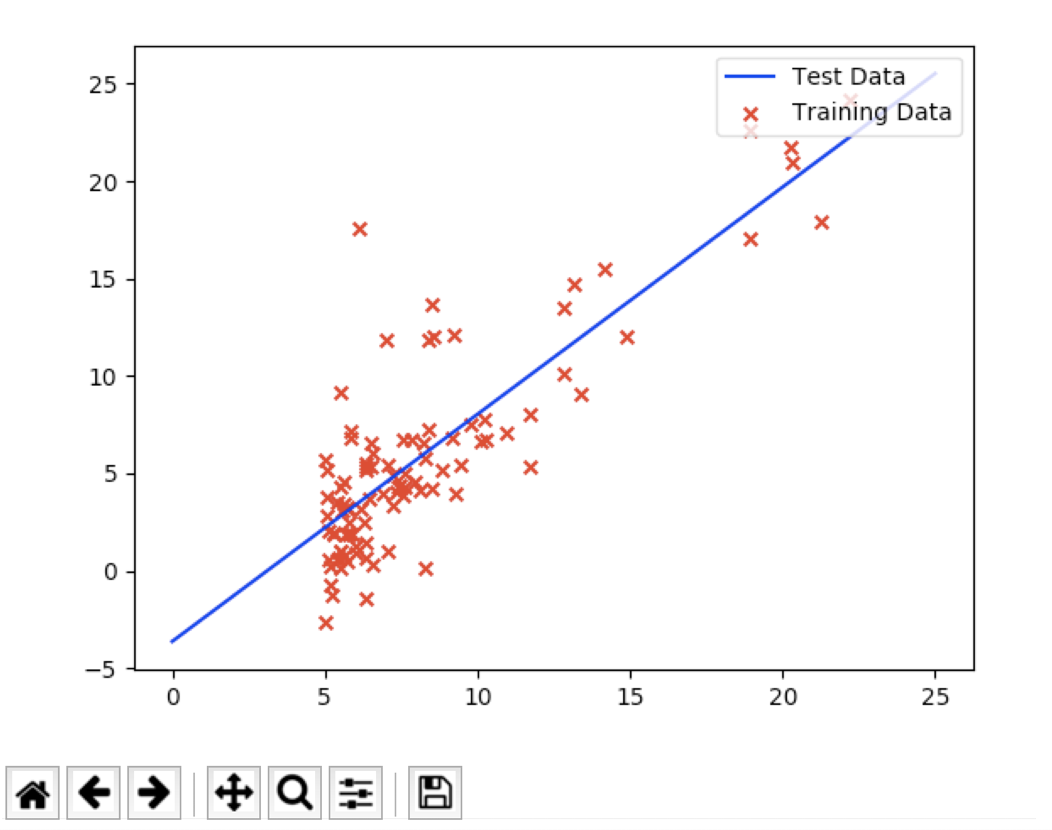
Andrew Ng机器学习课程,第一周作业,python版本的更多相关文章
- Stanford coursera Andrew Ng 机器学习课程第二周总结(附Exercise 1)
Exercise 1:Linear Regression---实现一个线性回归 重要公式 1.h(θ)函数 2.J(θ)函数 思考一下,在matlab里面怎么表达?如下: 原理如下:(如果你懂了这道作 ...
- Andrew Ng机器学习课程笔记(五)之应用机器学习的建议
Andrew Ng机器学习课程笔记(五)之 应用机器学习的建议 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7368472.h ...
- Andrew Ng机器学习课程笔记(四)之神经网络
Andrew Ng机器学习课程笔记(四)之神经网络 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7365730.html 前言 ...
- Andrew Ng机器学习课程笔记(三)之正则化
Andrew Ng机器学习课程笔记(三)之正则化 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7365475.html 前言 ...
- Andrew Ng机器学习课程笔记(一)之线性回归
Andrew Ng机器学习课程笔记(一)之线性回归 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7364598.html 前言 ...
- Andrew Ng机器学习课程笔记--week1(机器学习介绍及线性回归)
title: Andrew Ng机器学习课程笔记--week1(机器学习介绍及线性回归) tags: 机器学习, 学习笔记 grammar_cjkRuby: true --- 之前看过一遍,但是总是模 ...
- Andrew Ng机器学习课程笔记--汇总
笔记总结,各章节主要内容已总结在标题之中 Andrew Ng机器学习课程笔记–week1(机器学习简介&线性回归模型) Andrew Ng机器学习课程笔记--week2(多元线性回归& ...
- Andrew Ng机器学习课程笔记(六)之 机器学习系统的设计
Andrew Ng机器学习课程笔记(六)之 机器学习系统的设计 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7392408.h ...
- Andrew Ng机器学习课程笔记(二)之逻辑回归
Andrew Ng机器学习课程笔记(二)之逻辑回归 版权声明:本文为博主原创文章,转载请指明转载地址 http://www.cnblogs.com/fydeblog/p/7364636.html 前言 ...
- Andrew Ng机器学习课程6
Andrew Ng机器学习课程6 说明 在前面尾随者台大机器学习基石课程和机器学习技法课程的设置,对机器学习所涉及到的大部分的知识有了一个较为全面的了解,可是对于没有动手敲代码并加以使用的情况,基本上 ...
随机推荐
- Retry模式
Retry模式能够通过重复之前失败的操作来处理那些在调用远端服务或者网络资源的时候发生的一些可以预期的临时性的错误.Retry模式可以提高应用的稳定性. 问题 应用中,负责链接其他服务的组件必须要对环 ...
- POJ1035&&POJ3080&&POJ1936
字符串处理专题,很早就写好了然而忘记写blog了 1035 题意:给你一些单词作为字典.然后让你查找一些单词.对于每个单词,如果在字典中就输出它.否则输出所有它通过删除||增加||替换一个字符能得到的 ...
- Luogu P3370 【模板】字符串哈希
方法很多,hash,双hash(个人想到一种三hash),挂链,还有STL: map 乱搞 CODE #include<iostream> #include<map> #inc ...
- 【个人】爬虫实践,利用xpath方式爬取数据之爬取虾米音乐排行榜
实验网站:虾米音乐排行榜 网站地址:http://www.xiami.com/chart 难度系数:★☆☆☆☆ 依赖库:request.lxml的etree (安装lxml:pip install ...
- 大话Java中的哈希(hash)结构(一)
o( ̄▽ ̄)d 小伙伴们在上网或者搞程序设计的时候,总是会听到关于“哈希(hash)”的一些东西.比如哈希算法.哈希表等等的名词,那么什么是hash呢? 一.相关概念 1.hash算法:一类特殊的算法 ...
- 回溯-uva129
题目链接:https://vjudge.net/problem/UVA-129 题解: 这道题卡了一会儿的时间,一开始最大的问题是如何判断添加了一个字符之后,该字符串是不是一个困难的串,解决办法是:利 ...
- 现代OpenGL渲染管线介绍
原文摘选自 现代OpenGL渲染管线介绍 此文对最新的OpenGL做一个简单的介绍,如有理解错误,敬请指正.英文原文: https://glumpy.github.io/modern-gl.html ...
- 腾讯/阿里/百度 BAT人才体系的职位层级、薪酬、晋升标准
互联网圈有这么一句话:百度的技术,阿里的运营,腾讯的产品.那么代表互联网三座大山的BAT,内部人才体系有什么区别呢?今天老李就带领大家看一看~ ★ 腾讯 ★ 1. 职级 腾讯职级体系分6级,最低1 ...
- vector 简介
vector简介 vector是STL中最常见的容器,它是一种顺序容器,支持随机访问.vector是一块连续分配的内存,从数据安排的角度来讲,和数组极其相似, 不同的地方就是:数组是静态分配空间,一旦 ...
- 12.18daily_scrum
本软件中的最后一个界面——“关于”界面的设计已经开始进行,数据传输的内容也差不多进行过半,最主要的任务依旧在测试过程中,我们组接下来还是要大力加强测试的强度和数量,注意边际数据和错误数据的测试处理: ...
