P3756 [CQOI2017]老C的方块

题目链接

看到网格图+最优化问题，当然要想黑白染色搞网络流。不过这道题显然无法用黑白染色搞定。

仔细观察那四种图形，发现都是蓝线两边一定有两个格子，两个格子旁边一定还有且仅有一个格子。因此我们可以这么染色：

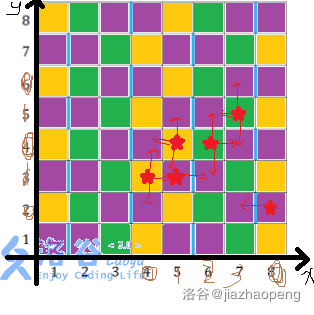
（图片有点丑）

染完色以后直接三分图匹配求最小割即可。

可以看出，横着4个一循环，纵向2个一循环，所以一共有8中不同的格子。实际上，我们只需要在那六个星星的位置进行判断即可。

关键代码：（S -> 黄 -> 紫 -> 绿 -> T）

for (register int i = 1; i <= n; ++i) {
	read(X[i]), read(Y[i]), read(W[i]);
	mp[X[i]][Y[i]] = i;
}
for (register int i = 1; i <= n; ++i) {
	int x = X[i], y = Y[i];
	int mx = x & 3, my = y & 1;
	if (mx == 1 && my == 1) {//purple
		int you = mp[x + 1][y];
		add(i, you, min(W[i], W[you]));
	} else if (mx == 0 && my == 0) {//purple
		int zuo = mp[x - 1][y];
		add(i, zuo, min(W[i], W[zuo]));
	} else if (mx == 0 && my == 1) {//yellow
		add(s, i, W[i]);
		int shang = mp[x][y + 1];
		add(i, shang, inf);
		int xia = mp[x][y - 1];
		add(i, xia, inf);
		int you = mp[x + 1][y];
		add(i, you, inf);
	} else if (mx == 1 && my == 0) {//yellow
		add(s, i, W[i]);
	int shang = mp[x][y + 1];
		add(i, shang, inf);
		int xia = mp[x][y - 1];
		add(i, xia, inf);
		int zuo = mp[x - 1][y];
		add(i, zuo, inf);
	} else if (mx == 2 && my == 0) {//green
		add(i, t, W[i]);
		int shang = mp[x][y + 1];
		add(shang, i, inf);
		int xia = mp[x][y - 1];
		add(xia, i, inf);
		int you = mp[x + 1][y];
		add(you, i, inf);
	} else if (mx == 3 && my == 1) {//green
		add(i, t, W[i]);
		int shang = mp[x][y + 1];
		add(shang, i, inf);
		int xia = mp[x][y - 1];
		add(xia, i, inf);
		int zuo = mp[x - 1][y];
		add(zuo, i, inf);
	}
}