[Fundamental of Power Electronics]-PART II-8. 变换器传递函数-8.2 变换器传递函数分析

8.2 变换器传递函数分析

接下来，让我们推导基本变换器传递函数中的极点，零点和渐近线增益的解析表达式。

8.2.1 示例：Buck-boost变换器的传递函数

Buck-boost变换器的小信号等效电路模型已经在7.2节中推导完成，其结果这里在图8.31中重新给出。让我们来推导并画出这个电路的控制-输出以及输入-输出的传递函数。

这个变换器包含两个独立的交流输入：控制输入$\hat{d}(s)$和直流输入$\hat{v}_{g}(s)$。交流输出电压的变化量$\hat{v}(s)$可以表示为这两个输入产生的量的叠加：

\[\hat{v} (s)=G_{vd}(s) \hat{d}(s)+G_{vg}(s) \hat{v}_{g}(s) \tag{8.126}
\]

因此，传递函数$G_{vd}(s)$和$G_{vg}(s)$可以被定义为：

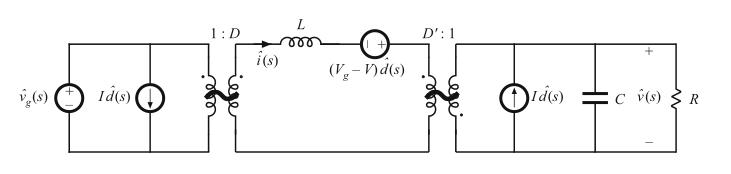
\[G_{vd}(s)=\cfrac{\hat{v}(s)}{\hat{d}(s)}|_{\hat{v}_{g}(s)=0}\ \ and\ \ G_{vg}(s)=\cfrac{\hat{v}(s)}{\hat{v}_{g}(s)}|_{\hat{d}(s)=0} \tag{8.127}
\]

Fig. 8.31 Buck–boost converter equivalent circuit derived in Sect. 7.2

为了确定输入输出传递函数$G_{vg}(s)$，如图8.32a，我们将$\hat{d}$相关的源置零。然后我们可以$v_{g}(s)$源和电感经过变压器移动，得到图8.32b所示的电路。利用分压公式可以得到传递函数$G_{vg}(s)$：

\[G_{vg}(s)=\cfrac{\hat{v}(s)}{\hat{v}_{g}(s)}|_{\hat{d}(s)=0}=-\cfrac{D}{D^{'}} \cfrac{(R// \cfrac{1}{sC})}{\cfrac{sL}{D^{'2}}+(R// \cfrac{1}{sC})} \tag{8.128}
\]

接下来，我们将并联结构展开，表示为有理分数：

\[\begin{matrix}
G_{vg}(s)=(-\cfrac{D}{D^{'}}) \cfrac{(\cfrac{R}{1+sRC})}{ \cfrac{sL}{D^{'2}}+(1+\cfrac{R}{1+sRC})} \\
=(-\cfrac{D}{D^{'}}) \cfrac{R}{R+\cfrac{sL}{D^{'2}}+\cfrac{s^{2} RLC}{D^{'2}}} \tag{8.129}
\end{matrix}
\]

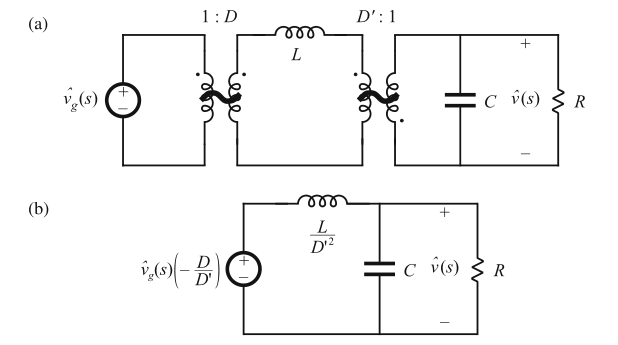
Fig. 8.32 Manipulation of buck–boost equivalent circuit to find the line-to-output transfer function

$G_{vg}(s)$: (a) set $\hat{d}(s)$ sources to zero; (b) push inductor and $\hat{v}_{g}(s)$ source through transformers

现在并没有完成——接下来是将表达式化为标准形式，使得分子多项式和分母多项式中$s^{0}$项的系数为1。这可以通过分子和分母同时除以$R$来实现：

\[G_{vg}(s)=(-\cfrac{D}{D^{'}}) \cfrac{1}{1+s\cfrac{L}{RD^{'2}}+s^{2}\cfrac{ LC}{D^{'2}}} \tag{8.130}
\]

因此，输入-输出传递函数中包含一个直流增益$G_{g0}$和一个二次极点对：

\[G_{vg}(s)=G_{g0}\cfrac{1}{1+\cfrac{s}{Q\omega_{0}}+(\cfrac{s}{\omega_{0}})^2} \tag{8.131}
\]

输入-输出传递函数的系数项解析表达式可以通过将式(8.130)和(8.131)中相同项系数相等而得到。直流增益为：

\[G_{g0}=-\cfrac{D}{D^{'}} \tag{8.132}
\]

通过令式(8.130)和(8.131)分母中$s^{2}$项的系数相等，可以得到：

\[\cfrac{1}{{\omega_{0}}^{2}}=\cfrac{LC}{D^{'2}} \tag{8.133}
\]

因此转折角频率为：

\[\omega_{0}=\cfrac{D^{'}}{\sqrt{LC}} \tag{8.134}
\]

令式(8.130)和(8.131)分母中$s$项系数相等，得到：

\[\cfrac{1}{Q \omega_{0}}=\cfrac{L}{D^{'2}R} \tag{8.135}
\]

利用式(8.134)消去$\omega_{0}$可以得到：

\[Q=D^{'}R \sqrt{\cfrac{C}{L}} \tag{8.136}
\]

式(8.132),(8.134)和(8.136)就是用来分析输入-输出传递函数的理想结果。这些表达式不仅在求解特征值$G_{g0},\omega_{0},Q$等的理论场合有用，其还在为满足给定特征值来选择$R,L,C$的元件值的设计场合有用。

由于图8.31中存在三个取决于$\hat{d}(s)$的项，因此控制-输出的传递函数推导变得复杂。一个比较好的方法就是像在图7.36中推导规范电路模型中一样来变换电路。这里使用另一种方法，叠加原理。第一部，我们将$\hat{v}_{g}$源置零。这简化了$1:D$变压器的输入端，并且我们得到了图8.33a所示的电路。接下来，我们将电感和$\hat{d}$源经过$D^{'}:1$变压器移动到右侧，从而得到了图8.33b。

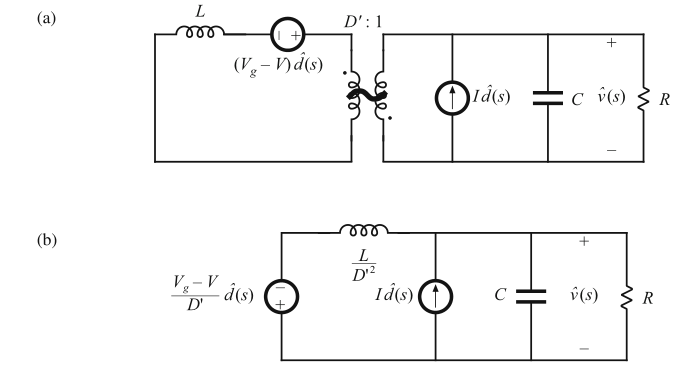
Fig. 8.33 Manipulation of buck–boost equivalent circuit to find the control-to-output transfer function $G{vd}(s)$: (a) set $\hat{v}_{g}$ source to zero; (b) push inductor and voltage source through transformer

图8.33b中包含了一个由$\hat{d}$控制的受控电压源和受控电流源。因此，传递函数$G_{vd}(s)$可以表示为这与两个源相关项的叠加。当电流源置零时(即：开路)，获得了图8.34a所示的电路。那么输出$\hat{v}(s)$可以表示为：

\[\cfrac{\hat{v}(s)}{\hat{d}(s)}=(-\cfrac{V_{g}-V}{D^{'}}) \cfrac{(R// \cfrac{1}{sC})}{\cfrac{sL}{D^{'2}}+(R// \cfrac{1}{sC})} \tag{8.137}
\]

当电压源被置零时(即：短路)，此时电路简化为图8.34b。输出$\hat{v}(s)$可以表示为：

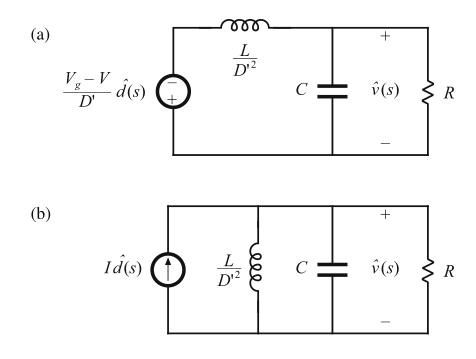
\[\cfrac{\hat{v}(s)}{\hat{d}(s)}=I(\cfrac{sL}{D^{'2}}//R//\cfrac{1}{sC}) \tag{8.138}
\]

Fig. 8.34 Solution of the model of Fig.8.33b by superposition: (a) current source set to zero; (b) voltage source set to zero

那么传递函数$G_{vd}(s)$就是(8.137)和(8.138)的和：

\[\begin{matrix}
G_{vd}(s)=(-\cfrac{V_{g}-V}{D^{'}}) \cfrac{(R// \cfrac{1}{sC})}{\cfrac{sL}{D^{'2}}+(R// \cfrac{1}{sC})} \\
+I(\cfrac{sL}{D^{'2}}//R//\cfrac{1}{sC})
\end{matrix} \tag{8.139}
\]

经过代数变换，可以得到如下的简化形式：

\[G_{vd}(s)=\cfrac{\hat{v}(s)}{\hat{d}(s)}|_{\hat{v}_{g}(s)=0}=(-\cfrac{V_{g}-V}{D^{'}}) \cfrac{1-s \cfrac{LI}{D^{'}(V_{g}-V)}}{1+s \cfrac{L}{D^{'2}R}+s^{2} \cfrac{LC}{D^{'2}}} \tag{8.140}
\]

这个方程具有如下的标准形式：

\[G_{vd}(s)=G_{g0} \cfrac{(1- \cfrac{s}{\omega_{z}})}{(1+ \cfrac{s}{Q \omega_{0}}+(\cfrac{s}{\omega_{0}})^2)} \tag{8.141}
\]

式(8.140)和(8.130)具有相同的分母，因此$G_{vd}(s)$和$G_{vg}(s)$具有如式(8.134)和(8.136)的相同的$\omega_{0}$和$Q$。其直流增益为：

\[G_{d0}=- \cfrac{V_{g}-V}{D^{'}}=\cfrac{V_{g}}{D^{'2}}=\cfrac{V}{DD^{'}} \tag{8.142}
\]

零点的角频率是通过令式(8.140)和(8.141)分子中的$s$的系数相等确定的。我们可以得到：

\[\omega_{z}= \cfrac{D^{'}(V_{g}-V)}{LI}=\cfrac{D^{'2}R}{DL} \ \ (RHP:右半平面) \tag{8.143}
\]

这个零点位于右半平面。通过下面两个直流关系式子使得(8.142)和(8.143)被简化：

\[\begin{matrix}
V=- \cfrac{D}{D^{'}}V_{g} \\
I=- \cfrac{V}{D^{'}R} \tag{8.144}
\end{matrix}
\]

式(8.134)(8.136)和(8.142)以及(8.143)构成了控制-输出传递函数的分析结果：特征值$\omega_{0},Q,G_{d0},\omega_{z}$的解析表达式。这些表达式可以用来选择元件的值从而获得给的特征期望值。

确定传递函数的特征值的解析表达式后，现在我们可以代入数值并构造bode图。假设我们得到了如下的值：

\[\begin{aligned}
& D=0.6 \\
& R=10 \Omega \\
& V_{g}=30V \\
& L=160 \mu H \\
& C=160 \mu F
\end{aligned} \tag{8.145}
\]

我们可以根据式(8.132),(8.134),(8.136)和(8.142)以及(8.143)来确定传递函数的特征值。结果为：

\[\begin{aligned}
& |G_{g0}|=\cfrac{D}{D^{'}}=1.5 \Rightarrow3.5\ dB \\
& |G_{d0}|=\cfrac{|V|}{DD^{'}}=187.5V \Rightarrow 45.5\ dB \\
& f_{0}=\cfrac{\omega_{0}}{2 \pi}=\cfrac{D^{'}}{2 \pi \sqrt{LC}}=400 Hz \\
& Q=D^{'}R \sqrt{\cfrac{C}{R}}=4 \Rightarrow 12\ dB \\
& f_{z}=\cfrac{\omega_{z}}{2 \pi}=\cfrac{D^{'2}R}{2 \pi DL}=2.65\ kHz
\end{aligned} \tag{8.146}
\]

图8.35给出了$G_{vd}$的幅值和相位的bode图。传递函数包含$45.5\ dBV$的直流增益，$Q$值为$4 \Rightarrow\ 12\ dB$的400Hz的谐振极点对，以及2.65 kHz的右半平面零点。一对谐振极点为高频相位渐近线贡献了-180°，而右半平面零点贡献了-90°。此外，Buck-boost的反相特性使得相位具有180°的反转，这并未包含在图8.35中。

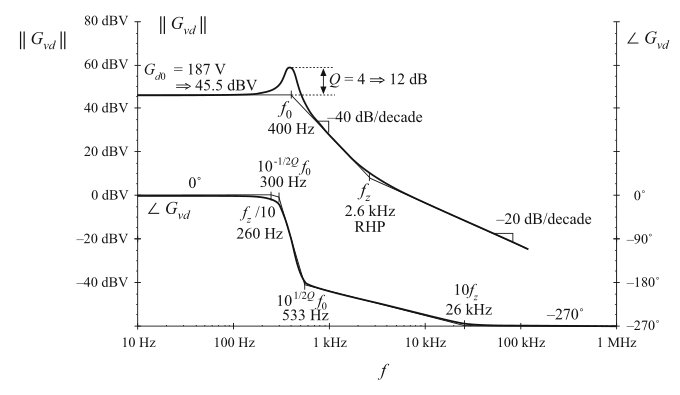
Fig. 8.35 Bode plot of the control-to-output transfer function $G_{vd}$, buck–boost converter example. Phase reversal owing to output voltage inversion is not included

输入-输出传递函数的幅值和相位bode图如图8.36所示。该传递函数在400 Hz处包含相同的谐振极点对，但并无右半平面零点。其直流增益$G_{g0}$等于变换器的直流变换比$M(D)$。同样的，由于Buck-boost变换器的输出反相特性带来的180°相位反转并未考虑在图内。

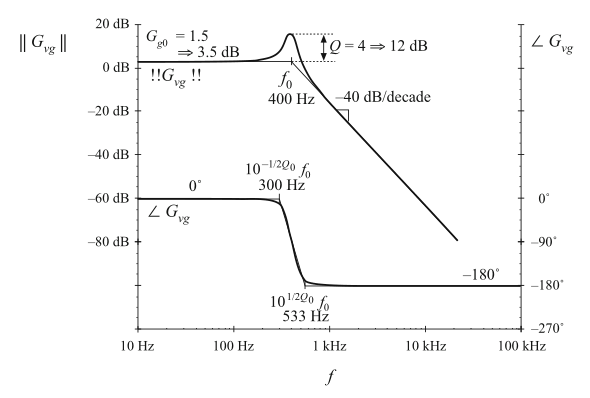
Fig. 8.36 Bode plot of the line-to-output transfer function $G_{vg}$, buck–boost converter example. Phase reversal owing to output voltage inversion is not included

8.2.2 一些基本CCM变换器的传递函数

表8.2总结了基本buck，boost和Buck-boost变换器的输入-输出传递函数的特征值。在不同的电路中，控制-输出传递函数都具有以下形式：

\[G_{vd}(s)=G_{d0} \cfrac{(1-\cfrac{s}{\omega_{z}})}{(1+\cfrac{s}{Q \omega_{0}}+(\cfrac{s}{\omega_{0}})^2)} \tag{8.147}
\]

并且，输入-输出传递函数都具有以下形式：

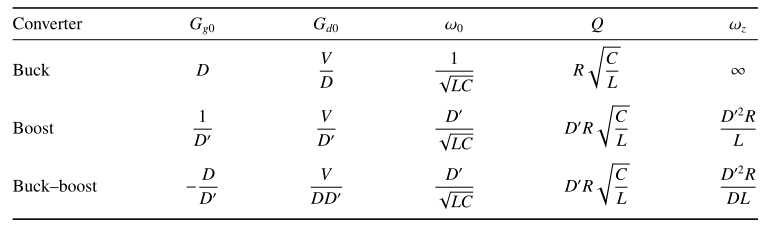
\[G_{vg}(s)=G_{g0}\cfrac{1}{(1+\cfrac{s}{Q \omega_{0}}+(\cfrac{s}{\omega_{0}})^2)} \tag{8.148}
\]

Table 8.2 Salient features of the small-signal CCM transfer functions of some basic dc–dc converters

在Boost和Buck-boost变换器的控制-输出传递函数中，包含两个极点和一个右半平面零点。而buck变换器的$G_{vd}(s)$中有两个极点但无零点。三个理想变换器的输入-输出传递函数中均只有两个极点，无零点。这些结果可以轻松适用于buck，boost和Buck-boost变换器的变压器隔离版本。除了引入匝比以外，变压器对传递函数$G_{vd}(s)$和$G_{vg}(s)$的影响可以忽略不计。例如，当全桥拓扑的变压器对称驱动时，其励磁电感不会对变换器的小信号传递函数产生动态影响。同样，当正激变换器的励磁电感由输入电压重置(如图6.24或6.29)，那么其影响也可以忽略不计。在所有基于buck，boost和Buck-boost的变压器隔离式变换器中，输入-输出传递函数中应该乘以变压器匝比。(8.147)和(8.148)的传递函数以及表8.2列出的参数可以直接使用。

8.2.3 变换器传递函数中RHP零点的物理来源

图8.37包含了说明右半平面零点特性的框图。在低频段，$(s/\omega_{z})$具有可忽略的幅值，因此$u_{out} \approx u_{in}$。在高频段$(s/\omega_{z})$幅值远大于1，$u_{out} \approx -(s/\omega_{z})u_{in}$。负号会导致高频的相位反转。对瞬态响应的影响是：输出的初值趋向于终值的反方向。

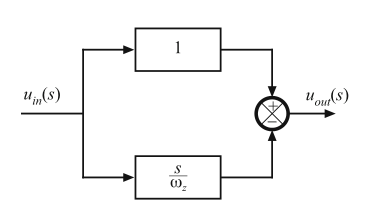
Fig. 8.37 Block diagram having a right half-plane zero transfer function, as in Eq. (8.32), with $ω_0= ω_z$

我们已经知道，如图8.38所示的boost和Buck-boost变换器的控制-输出传递函数存在RHP零点。占空比阶跃变化的典型瞬态响应波形如图8.39所示。对于这个例子，变换器最初在$d=0.4$和$d^{'}=0.6$的稳态下工作。图中给出了稳态电感电流$i_{L}(t)$，输出电压$v(t)$以及二极管电流$i_{D}(t)$。平均二极管电流为：

\[\begin{matrix}
<i_{D}>_{T_{s}}=d^{'}<i_{L}>_{T_{s}} \tag{8.149}
\end{matrix}
\]

当变换器工作于稳态时，根据电容电荷平衡，该平均二极管电流等于负载的直流电流。在$t=t_{1}$时，占空比增加到$d=0.6$，$d^{'}=0.4$。由式(8.149)给出的平均二极管电流减小，输出电容开始放电。输出电压的幅值如图所示在最开始会下降。

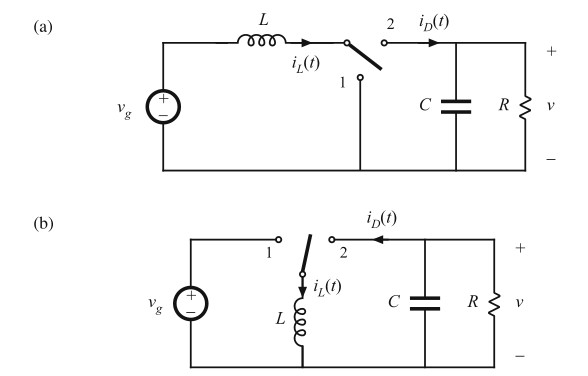
Fig. 8.38 Two basic converters whose CCM control-to-output transfer functions exhibit RHP zeroes: (a) boost, (b) buck–boost

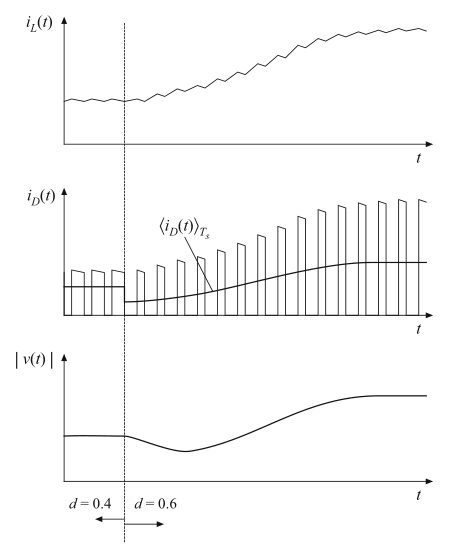
Fig. 8.39 Waveforms of the converters of Fig.8.38, for a step response in duty cycle. The average

diode current and output voltage initially decrease, as predicted by the RHP zero. Eventually, the inductor current increases, causing the average diode current and the output voltage to increase

增大的占空比使得电感电流缓慢增加，因此平均二极管电流最终将超过其在$d=0.4$时的平衡值。输出电压幅值最终会增加到对应于$d=0.6$时的新的平衡值。

右半平面零点的存在将会破坏较宽带宽的反馈回路的稳定性，因为在瞬态期间，输出值在开始会朝着错误的方向偏差。下一章将讨论用于反馈回路稳定性的相位裕度的测试。当右半平面零点存在时，在具有比较宽带宽的常规单环反馈系统中很难获得足够的相位裕量。右半平面零点的预测以及为什么控制CCM的boost和Buck-boost变换器的反馈环路将趋于振荡的解释是平均变换器建模的早期贡献之一。