字节笔试题 leetcode 69. x 的平方根

更多精彩文章请关注公众号：TanLiuYi00

题目

解题思路

题目要求非负整数 x 的平方根，相当于求函数 y = √x 中 y 的值。

函数 y = √x  图像如下：

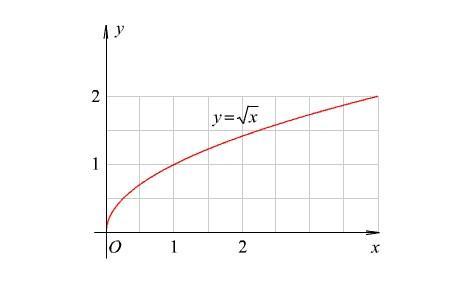
从上图中，可以看出函数是单调递增的，满足二分查找的条件（区间是有序的），所以可以用二分查找去做。

解题步骤

• 比较 mid * mid 跟 x 的大小，相等则直接返回 mid，否则就去以 mid 为分割点的左右区间查找，直到不满足循环循环条件（left == right + 1 或 left == right 究竟是哪一个主要跟循环条件有关，请看后面的分析）就退出。

• 由于非负整数 x（当 x ≠ 0 时） 的平方根一定是落在区间 [1, x/2 + 1]，所以左右边界分别取 1 和 x/2 + 1，而不分别取 0 和 x，这样可缩小查找范围。

• 为了防止 mid * mid 太大而发生整型溢出，取 mid 跟 x/mid 比较。

说明

右边界 right 取 x/2 + 1，而不取 x/2，这是因为当 x = 1 时，right 如果取 x/2，由于 x/2 会向下取整使得 x/2 = 0，此时 left = 1 大于 right = 0，以至于直接跳出循环，导致 1 的平方根为 0，这明显是错误的。

Show me the Code

int mySqrt(int x){
    int left = 1, right = x / 2 + 1;
    //  循环不变量  始终维持在区间 [left, right] 中查找，当 left = right + 1 时，区间为空，查找结束
    //  当 left == right 时，区间 [left, right] 依然有效
    while (left <= right) {
        //  防止溢出
        int mid = left + ((right - left) >> 1);
        //  mid 大于 √x ，在 mid 前半区间 [left, mid - 1] 中查找，不是 [left, mid]
        //  是因为会当查找到 target 时，直接返回 mid，所以没必要再考虑 mid
        if (mid > x / mid) {
            right = mid - 1;
        //  mid 小于 √x ，在 mid 后半区间 [mid + 1, right] 中查找
        } else if (mid < x / mid) {
            left = mid + 1;
        //  mid 等于 √x ，代表查找到 target，则直接返回
        } else {
            return mid;
        }
    }

    return right;
}

补充说明

如果没有出现 mid == x / mid 的情况，最后到底是 return right 还是 return left？
1、可以通过调试得出；

2、循环结束的条件是 left = right + 1，示例中提示了当 x = 8，其平方根是 2，有点类似于向下取整的意思，所以是 return right 。

进一步补充

可能有些童鞋会问到，上面代码中循环的条件为何是 left <= right 而不是 left < right，其实这两个条件都可以，主要区别在于：

循环结束的条件不一样，前者是 left = right + 1 后者是 left = right，即前者当 left = right + 1 时，查找区间 [left, right] 为空，后者当 left = right 时，查找区间 [left, right) 为空。

定义的右边界取值不一样，前者右边界取值为 x / 2 + 1，后者可为 x / 2 + 2。

这里会提到一个循环不变量的概念：

循环不变量

1. 初始化：它在循环的第一轮迭代开始之前，应该是正确的。

2. 如果在循环的某一次迭代开始之前它是正确的，那么，在下一次迭代开始之前，它也应该保持正确。

3. 当循环结束时，不变式给了我们一个有用的性质，它有助于表明算法是正确的。

所以本题循环的条件可以是 left <= right 也可以是 left < right，关键是查找的过程中需要一直维护查找区间 [left, right] 或 [left, right)。

下面补充一个循环条件为 left < right 的代码。

最后返回的是 right - 1，这是因为:

定义的查找区间是左闭右开[left, right)，取不到右边界 right；当 left == right 时，循环退出，由于 right 取不到并且平方根有点向下取整的意味，所以取 right - 1；

通过调试也能得出。

Show me the Code

int mySqrt(int x){
    int left = 1, right = x / 2 + 2;
    //  循环不变量 始终维持在区间 [left, right) 中查找，当 left = right 时，区间为空，查找结束
    while (left < right) {
        //  防止溢出
        int mid = left + ((right - left) >> 1);
        //  mid 大于 √x ，在 mid 前半区间 [left, mid) 中查找
        if (mid > x / mid) {
            right = mid;
        //  mid 小于 √x ，在 mid 后半区间 [mid + 1, right) 中查找
        } else if (mid < x / mid) {
            left = mid + 1;
        //  mid 等于 √x ，代表查找到 target，则直接返回
        } else {
            return mid;
        }
    }
    return right - 1;
}

更多精彩文章可关注公众号：TanLiuYi00