三角函数与缓入缓出动画及C#实现（图文讲解）

---

日常经常能看到缓入缓出的动画效果，如：

1，带缓入缓出效果的滚动条：

2，带缓入缓出效果的呼吸灯：

像上面这种效果，就是用到了三角函数相关的知识，下面将从头开始一步步去讲解如何实现这种效果。

---

一、基础知识

（一）三角函数

常用的三角函数有正弦函数（sin）、余弦函数（cos）、正切函数（tan）。在动画效果中常用的是正弦函数和余弦函数，由于两者可以互相转化，所以本文将以正弦函数来进行讲解。

如下图所示直角三角形ABC：

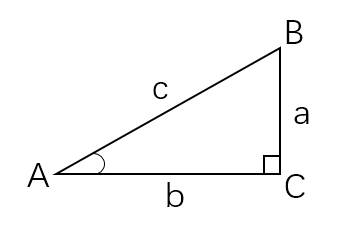
则：

sin(A)=a/c

即：角A的正弦值=角A的对边/斜边

（二）正弦曲线

将三角函数与动画桥接起来的便是三角函数曲线。

以正弦函数为例，其正弦曲线公式为：y = A*sin(B*x + C) + D

其中y、x分别是纵坐标、横坐标。

1，在默认状态时，即：y=sin(x) 时，其曲线如下图所示：

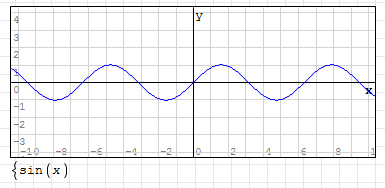
2，正弦曲线公式中的参数 “A” 控制曲线的振幅，A 值越大，振幅越大，A 值越小，振幅越小。

如：y=2*sin(x)，其曲线如下图所示（蓝线为 y=sin(x)）：

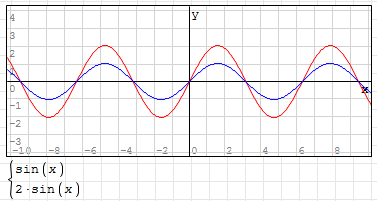
3，参数 “B" 控控制曲线的周期，B 值越大，那么周期越短，B 值越小，周期越长。

如：y=sin(2x)，其曲线如下图所示（蓝线为 y=sin(x)）：

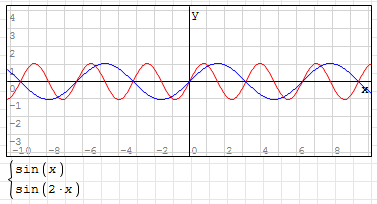
4，参数 “C" 控控制曲线左右移动，C 值为正数，曲线左移，C 值为负数，曲线右移；

如：y=sin(x+1)，其曲线如下图所示（蓝线为 y=sin(x)）：

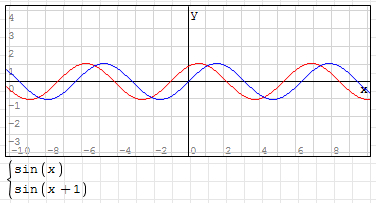
5，参数 “D" 控控制曲线上下移动。D 值为正数，曲线上移，D 值为负数，曲线下移；

如：y=sin(x)+1，其曲线如下图所示（蓝线为 y=sin(x)）：

（三）角度与弧度

因为在使用代码去计算正弦值时，其单位一般是弧度，像C#中的”Math.Sin()“函数，而直观的效果却是角度，所以需要讲解一下角度与弧度。

1，角度

定义：两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之中的一个时，两条射线的夹角的大小为1度。

示意图如下：

2，弧度

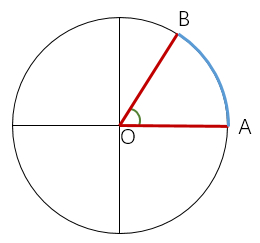
定义：弧度：两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时，两条射线的夹角大小为1弧度。

示意图如下：

其中：AB=OA=r

3，角度与弧度的差别

最基本的差别在于角所对的弧长大小不同。度的是等于圆周长的360分之中的一个，而弧度的是等于半径。

4，角度与弧度的转换

因为：弧度角=弧长/半径

所以：

a，周角（360度）=周长/半径＝2πr/r=2π

b，平角（180度）=π

由b可知：180度=π弧度

所以：

c，1度＝π/180 弧度（≈0.017453弧度）
d，1弧度＝180/π 度（≈57.3度）

可得转换公式：

弧度=度*π/180
度=弧度*180/π

---

三、动画实现

实现的思路简单而言便是利用正弦曲线的”y“和”x“值的变化。对于缓入缓出动画，就是速度的变化。

速度的定义和公式：速度在数值上等于物体运动的位移跟发生这段位移所用的时间的比值。速度的计算公式为v=Δs/Δt

控制速度，无非是”距离“与”时间“这两个量的变化。

在实现应用中，往往不会同时变化两个量，而是固定一个量，变化一个量。

在实际程序实现时，一般是固定“时间”，只变化“距离”。此处的”时间“可以理解为”时间间隔“。即在时间间隔不变的情况下，需要考虑每个时间间隔内运行的距离。

那么在正弦曲线上的体现便是等x间隔下，y的取值。

（一）简单实现

（1）实现思路：

1，通过y=sin(x)的曲线可知：y值的范围是（-1~+1）

2，将曲线上移，上移距离为1，即：y=sin(x)+1，此时y值的范围：（0~2）

3，为使y值范围变为（0~1），对函数除2，即：y=(sin(x)+1)/2

如图（蓝线为 y=sin(x)）：

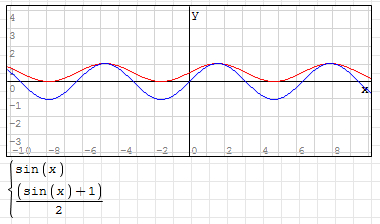
4，将y值乘以缓入缓出动画的摆动距离

（2）C#实现：

1，控件布局及属性

2，核心代码

 void pShowD()
 {
     //i是度数，不是弧度
     int i = ;
     //移动距离要减去滑块本身的宽度
     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
     while (true)
     {
         i++;
         if (i > )
         {
             //一个周期是360度
             i = ;
         }
         //固定时间间隔
         Thread.Sleep();
         //通过公式：弧度=度*π/180，将度数i转为Math.Sin()所需要的弧度数
         double dz = dMoveDistance * ( + Math.Sin(i * Math.PI / )) / ;
         pSetLeft(Convert.ToInt32(dz));

     }
 }

 void pSetLeft(int i)
 {
     if (panel_Slider.InvokeRequired)
     {
         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
     }
     else
     {
         panel_Slider.Left = i;
     }
 }

简单实现

3，运行效果

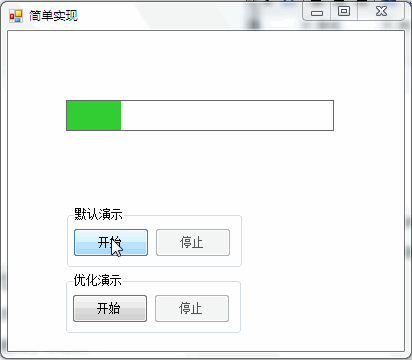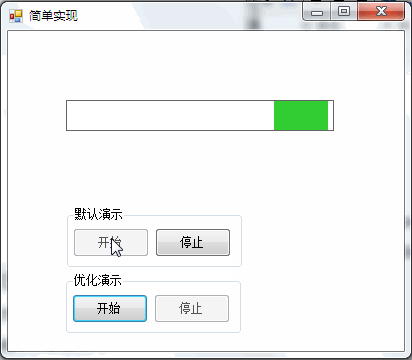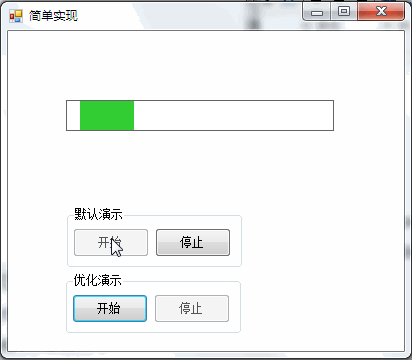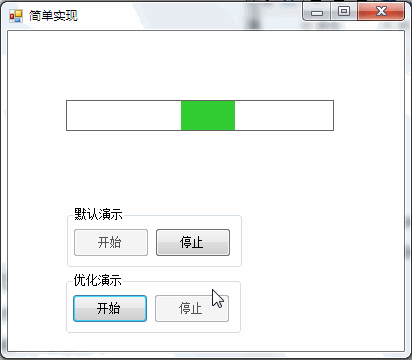
（二）简单实现优化

通过观察上面的实现，可以发现虽然实现了缓入缓出效果，但是其”滑块“（panel_Slider）的起始位置却不是最左侧，而是从中间开始。

根据上面的公式也可以看出来，当x=0时，y=(sin(x)+1)/2=1/2，即：整个摆动距离的二分之一。

（1）优化思路

为了让滑块从最左侧开始，则需要将曲线向右移动，移动距离是π/2。

其曲线公式变为：y=(sin(x-π/2)+1)/2

如图（蓝线为 y=sin(x)）：

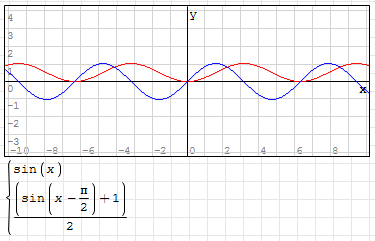
（2）C#实现

1，布局同上。

2，核心代码

 void pShowD2()
 {
     //i是度数，不是弧度
     int i = ;
     //移动距离要减去滑块本身的宽度
     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
     while (true)
     {
         i++;
         if (i > )
         {
             //一个周期是360度
             i = ;
         }
         //固定时间间隔
         Thread.Sleep();
         //通过公式：弧度=度*π/180，将度数i转为Math.Sin()所需要的弧度数
         //因为i是度数，所以是（i-90）
         double dz = dMoveDistance * ( + Math.Sin((i-) * Math.PI / )) / ;
         pSetLeft(Convert.ToInt32(dz));

     }
 }

 void pSetLeft(int i)
 {
     if (panel_Slider.InvokeRequired)
     {
         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
     }
     else
     {
         panel_Slider.Left = i;
     }
 }

简单实现（优化）

3，运行效果

（三）扩展实现

在实际应用中，动画往往需要在”固定时间“内完成。

以前面实现为例，使滑块从左端滑到右端的时长固定为1秒。该怎么实现呢？

（1）实现思路

整体思路与之前的并没有什么大的区别，仍是固定”时间“，变化”距离“。

在前面的”简单实现（优化）“的基础上，需要增加下面的一些修改和补充：

1，假设”时间间隔“为：Interval，那么，在指定的1秒内，共会变化（Step=1/Interval）次。

2，那么，每次变化时度数的变化便不再是”1“，又一个周期是滑块一个来回，所以，第次变化的度数便是：Per=2π/2*Step=180/Step。

（2）C#实现

在实现时加入了匀速的对比。

1，布局及属性

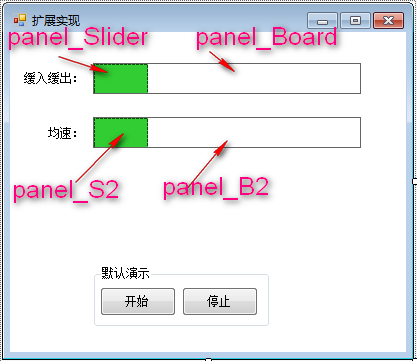
2，核心代码

 void pShowD2()
 {
     //当前滑块的位置
     double d = ;
     //true/false：向右滑/向左滑
     bool bToRight = true;
     //时间间隔，单位：ms
     int iInterval = ;
     //从左到右所需要的总时间，单位：ms
     int iAnimateTime = ;
     //移动距离要减去滑块本身的宽度
     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
     //需要变化的次数
     double dStep = Convert.ToDouble(iAnimateTime) / iInterval;
     //每次变化所增加的距离
     double dPerX = dMoveDistance / dStep;
     while (true)
     {
         d = bToRight ? d + dPerX : d - dPerX;
         if (d > dMoveDistance)
         {
             bToRight = false;
         }
         if (d < )
         {
             bToRight = true;
         }

         Thread.Sleep(iInterval);
         int iZ = Convert.ToInt32(d);
         pSetLeft2(iZ);

     }
 }
 void pSetLeft2(int i)
 {
     if (panel_S2.InvokeRequired)
     {
         panel_S2.Invoke(new Action<int>(pSetLeft2), new object[] { i });
     }
     else
     {
         panel_S2.Left = i;
     }
 }

1，匀速

 void pShowD()
 {
     //d是度数，不是弧度
     double d = ;
     //时间间隔，单位：ms
     int iInterval = ;
     //从左到右所需要的总时间，单位：ms
     int iAnimateTime = ;
     //移动距离要减去滑块本身的宽度
     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
     //需要变化的次数
     double dStep = Convert.ToDouble(iAnimateTime) / iInterval;
     //每次变化所增加的度数
     double dPer = 180.0 / dStep;
     while (true)
     {
         d += dPer;
         if (d > )
         {
             //一个周期是360度
             d = ;
         }
         //固定时间间隔
         Thread.Sleep(iInterval);
         //通过公式：弧度=度*π/180，将度数i转为Math.Sin()所需要的弧度数
         double dz = dMoveDistance * ( + Math.Sin((d - ) * Math.PI / )) / ;
         pSetLeft(Convert.ToInt32(dz));

     }
 }

 void pSetLeft(int i)
 {
     if (panel_Slider.InvokeRequired)
     {
         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
     }
     else
     {
         panel_Slider.Left = i;
     }
 }

2，缓入缓出

3，运行效果

---

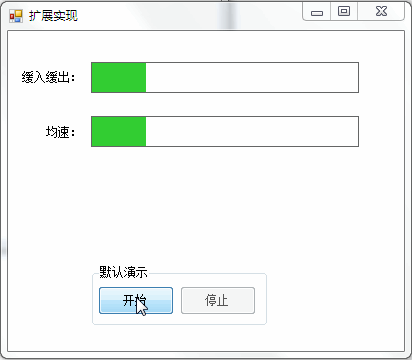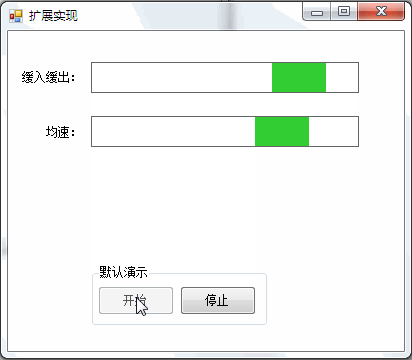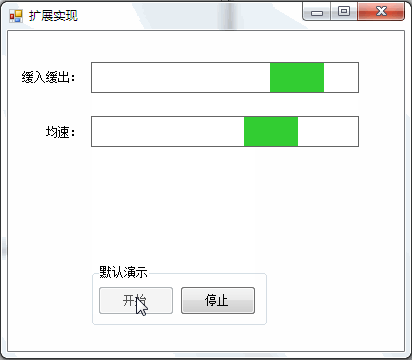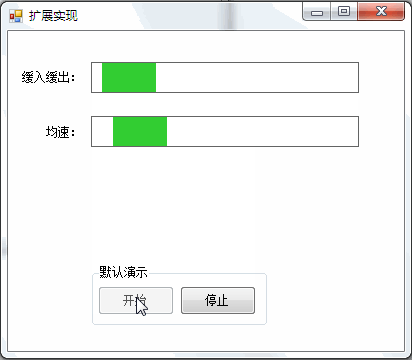
四、结束语

本篇主要讲的是三角函数与缓入缓出动画，但三角函数在动画中的作用不仅仅如此，比如直接使用正弦曲线的形状来绘制波浪效果——在充电、进度条等地方可以使用该效果。

而且即然知道在曲线在动画中的作用，那么便可以通过不同的函数曲线实现不同的动画效果，比如另一个非常好用的”贝塞尔曲线“，可以实现更复杂、更优雅的动画效果。

如有错误和不足之处欢迎大家批评指正。