广义高斯分布(GGD)和非对称广义高斯分布(AGGD)

《No-Reference Image Quality Assessment in the Spatial Domain》，BRISQUE。

1. 广义高斯分布，generalized Gaussian distribution，GGD

1.1 描述

零均值的广义高斯分布如下：

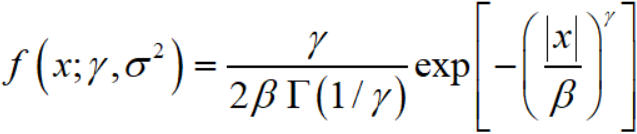
其中

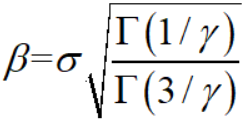
而 Γ(·) 是gamma函数。

形状参数 γ 控制分布的“形状”，而 σ² 控制方差。

例如另 γ = 2 就会得到零均值的高斯分布：

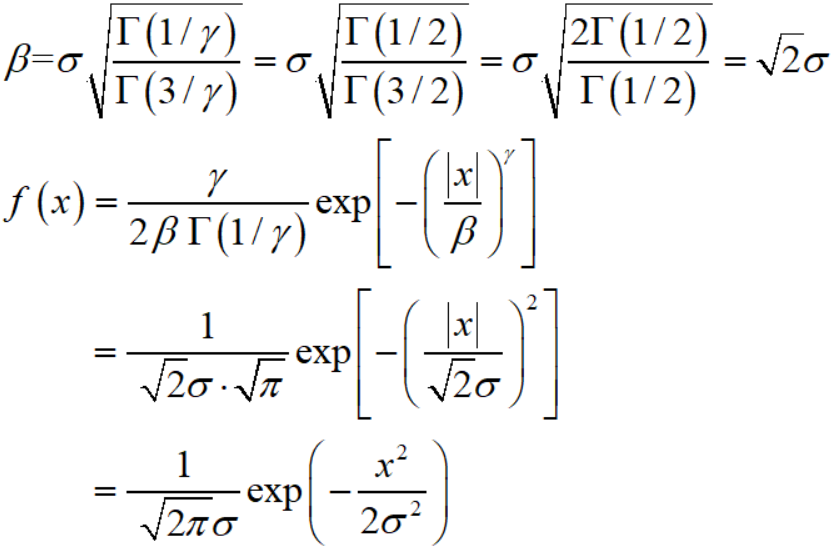
首先记

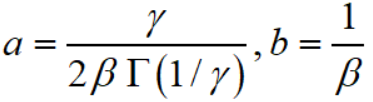
则

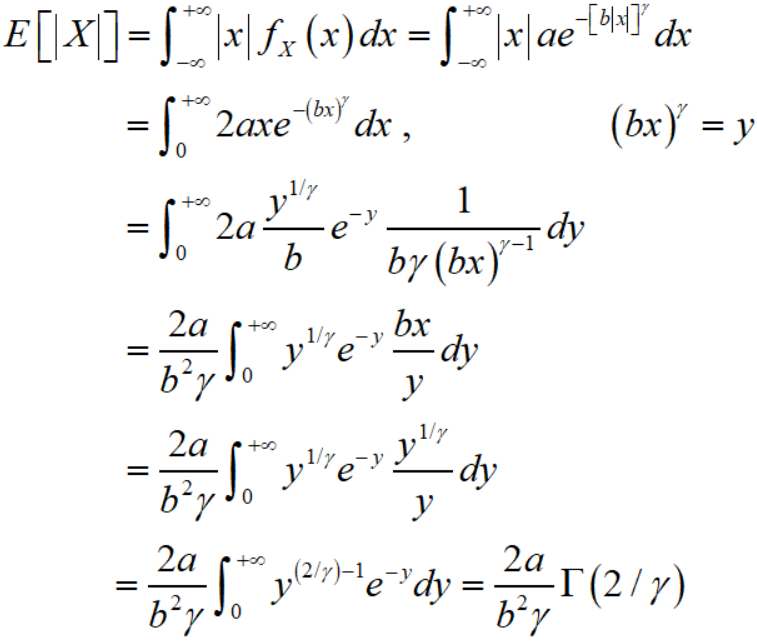
因此

就得到了一个比函数：

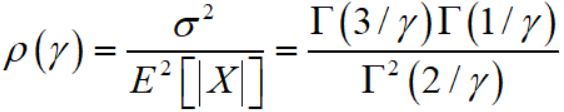
1.2 参数估计方法

对于零均值广义高斯分布，计算估计值：

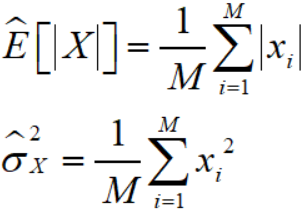
然后就有

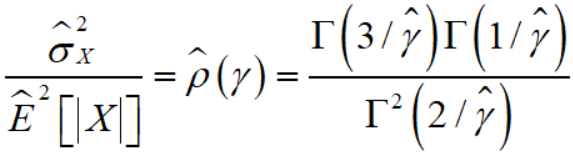
在知道了 ρ(γ) 的估计值之后，就很容易通过枚举的方式来估计 γ。

1.3 代码

参考BRISQUE中给出的源代码：

function [gamparam sigma] = estimateggdparam(vec)
gam                              = 0.2:0.001:10;
r_gam                            = (gamma(1./gam).*gamma(3./gam))./((gamma(2./gam)).^2);

sigma_sq                         = mean((vec).^2);
sigma                            = sqrt(sigma_sq);
E                                = mean(abs(vec));
rho                              = sigma_sq/E^2;
[min_difference, array_position] = min(abs(rho - r_gam));
gamparam                         = gam(array_position);

2. 非对称广义高斯分布，asymmetric generalized Gaussian distribution，AGGD

2.1 描述

零均值的非对称广义高斯分布如下：

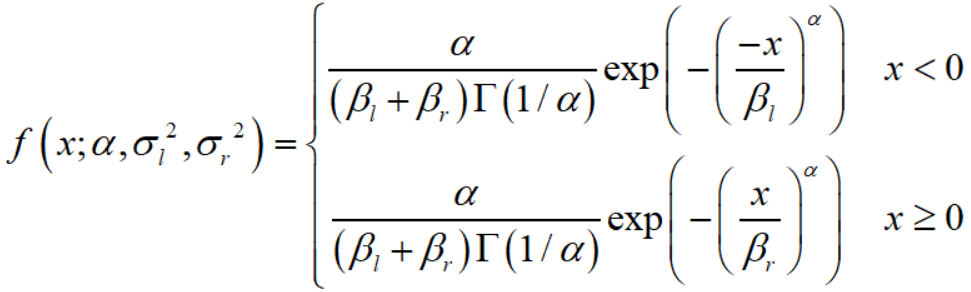
其中

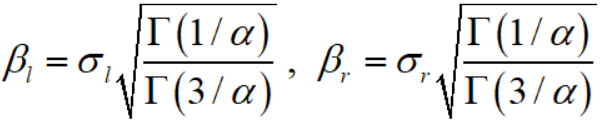
形状参数 α 控制分布的“形状”，而 σ_l² 和 σ_r² 是缩放参数，它们控制模式两边的扩散程度。当 σ_l² = σ_r² 的时候，AGGD退化成GGD。

参考论文《MULTISCALE SKEWED HEAVY TAILED MODEL FOR TEXTURE ANALYSIS》的做法：

记

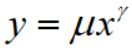
则

因此

所以记

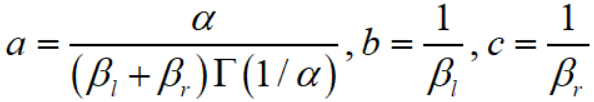
就有

类似地

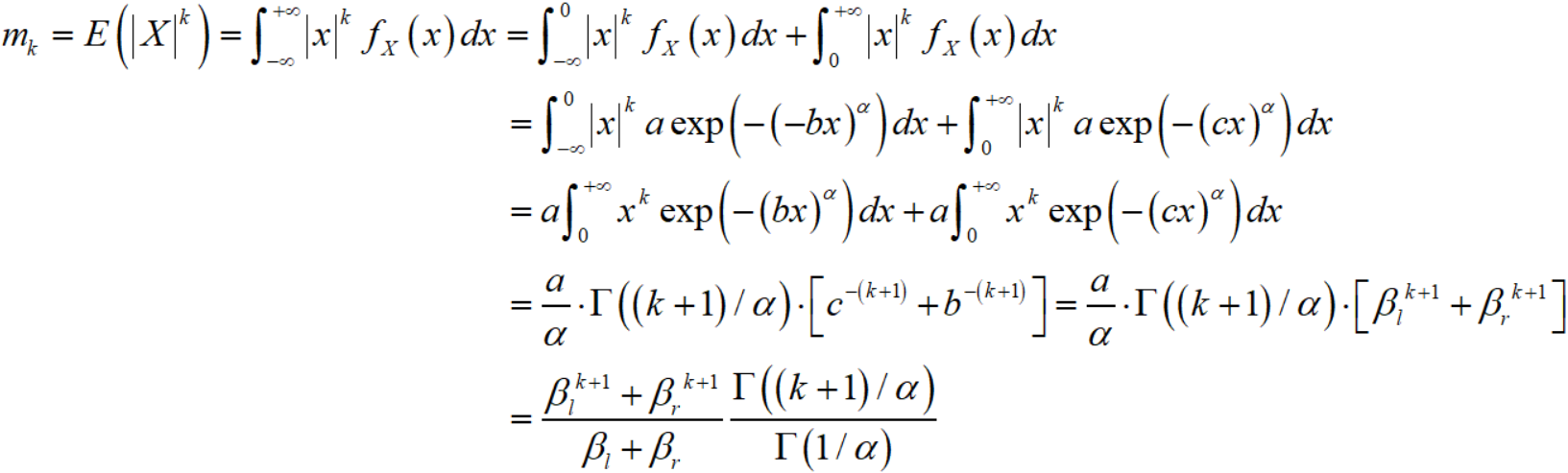
然后计算比值：

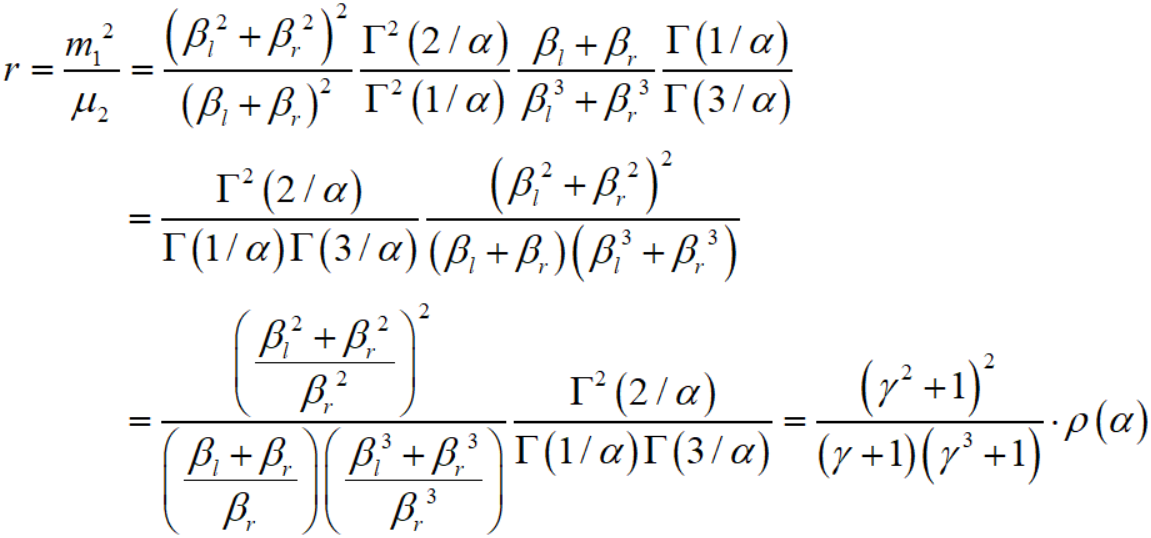
其中

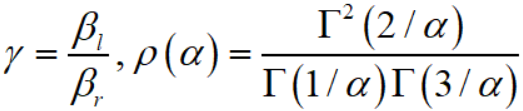
2.2 参数估计方法

首先估计 σ_l² 和 σ_r² ：

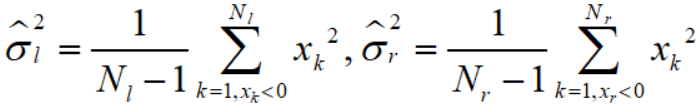
所以

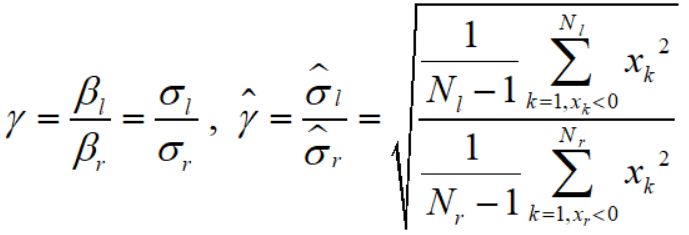
而 r 的一个无偏估计是

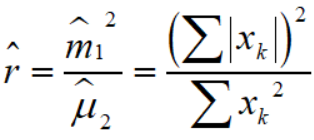
所以就可以

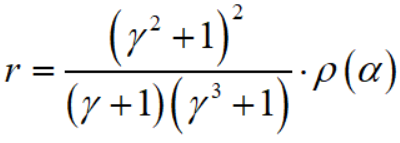
求得

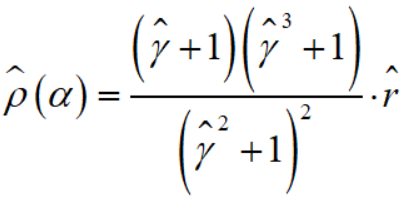
然后就和上文的GGD的方法一样，枚举求出最优的 α 就可以了。

2.3 代码

也是来自BRISQUE的matlab代码：

function [alpha leftstd rightstd] = estimateaggdparam(vec)
gam   = 0.2:0.001:10;
r_gam = ((gamma(2./gam)).^2)./(gamma(1./gam).*gamma(3./gam));

leftstd            = sqrt(mean((vec(vec<0)).^2));
rightstd           = sqrt(mean((vec(vec>0)).^2));
gammahat           = leftstd/rightstd;
rhat               = (mean(abs(vec)))^2/mean((vec).^2);
rhatnorm           = (rhat*(gammahat^3 +1)*(gammahat+1))/((gammahat^2 +1)^2);
[min_difference, array_position] = min((r_gam - rhatnorm).^2);
alpha              = gam(array_position);