java实现BellmanFord算法

1 问题描述

何为BellmanFord算法？

BellmanFord算法功能：给定一个加权连通图，选取一个顶点，称为起点，求取起点到其它所有顶点之间的最短距离，其显著特点是可以求取含负权图的单源最短路径。

BellmanFord算法思想：

第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。

第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。

第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：如果d（v） > d (u) + w(u,v)，则返回false，表示途中存在从源点可达的权为负的回路。

2 解决方案

2.1 具体编码

Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E)。（V为给定图的顶点集合，E为给定图的边集合）

本文编码思想主要参考自文末参考资料1中博客，想要进一步了解，可以参考文末参考资料。

首先看下代码中所使用的连通图（PS：改图为无向连通图，所以每两个顶点之间均有两条边）：

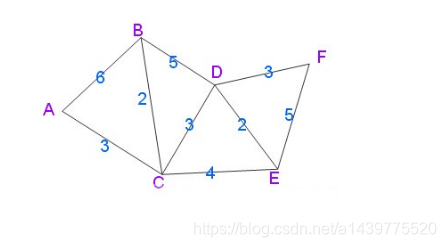
现在求取顶点A到其它所有顶点之间的最短距离

package com.liuzhen.chapter9;

import java.util.Scanner;

public class BellmanFord {

    public  long[] result;       //用于存放第0个顶点到其它顶点之间的最短距离

    //内部类，表示图的一条加权边
    class edge {
        public int a;   //边的起点
        public int b;   //边的终点
        public int value;  //边的权值

        edge(int a, int b, int value) {
            this.a = a;
            this.b = b;
            this.value = value;
        }
    }
    //返回第0个顶点到其它所有顶点之间的最短距离
    public  boolean getShortestPaths(int n, edge[] A) {
        result = new long[n];
        for(int i = 1;i < n;i++)
            result[i] = Integer.MAX_VALUE;  //初始化第0个顶点到其它顶点之间的距离为无穷大，此处用Integer型最大值表示
        for(int i = 1;i < n;i++) {
            for(int j = 0;j < A.length;j++) {
                if(result[A[j].b] > result[A[j].a] + A[j].value)
                    result[A[j].b] = result[A[j].a] + A[j].value;
            }
        }
        boolean judge = true;
        for(int i = 1;i < n;i++) {   //判断给定图中是否存在负环
            if(result[A[i].b] > result[A[i].a] + A[i].value) {
                judge = false;
                break;
            }
        }
        return judge;
    }

    public static void main(String[] args) {
        BellmanFord test = new BellmanFord();
        Scanner in = new Scanner(System.in);
        System.out.println("请输入一个图的顶点总数n和边总数p：");
        int n = in.nextInt();
        int p = in.nextInt();
        edge[] A = new edge[p];
        System.out.println("请输入具体边的数据：");
        for(int i = 0;i < p;i++) {
            int a = in.nextInt();
            int b = in.nextInt();
            int value = in.nextInt();
            A[i] = test.new edge(a, b, value);
        }
        if(test.getShortestPaths(n, A)) {
            for(int i = 0;i < test.result.length;i++)
                System.out.print(test.result[i]+" ");
        } else
            System.out.println("给定图存在负环，没有最短距离");
    }

}

运行结果：

请输入一个图的顶点总数n和边总数p：
18
请输入具体边的数据：
1 6
2 3
2 2
3 5
3 3
4 4
4 2
5 3
5 5
0 6
0 3
1 2
1 5
2 3
2 4
3 2
3 3
4 5
5 3 6 7 9