汇编语言、与C语言、实现--汉诺塔--

题意描述：  

用汇编语言实现汉诺塔。只需要显示移盘次序，不必显示所移盘的大小，例如: X>Z,X>Y,Z>Y,X>Z,....。

（n阶Hanoi塔问题）假设有三个分别命名为X、Y、Z的塔座，在塔座X上插有n个直径大小各不相同、依小到大编号为1，2，…，n的圆盘。现要求将X轴上的n个圆盘移至塔座Z上并仍按同样顺序叠排，圆盘移动时必须遵循下列规则：

1）每次只能移动一个圆盘；

2）圆盘可以插在X、Y、Z中的任一塔座上；

3）任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。

汉诺塔的实现，用C语言来解释就是函数递归调用实现

如果转为汇编实现，就直接进入栈进行相应的操作就行（当然你也可以用汇编语言宏实现高级的递归调用..)

C语言方式：

void move(char one,char three){    //one 移到thre

printf("%c--->%c",one,three);

}

void HANOI(int n,char one,char two,char three){

if(n==){                          //如果只有一个圆盘，直接将这个圆盘从one移到three

move(one,three);
}

else{                                 //如果大于一个圆盘

HANOI(n-,one,three,two); //首先将n-1个从one经过three移到two上，此时one上剩最大的一个圆盘

move(one,three);               //将最大的圆盘从one移到three上

HANOI(n-,two,one,three); //之后将n-1个从two经过one移到three上，完成。

}

}               // end of void

HANOI(,'X','Y','Z');  //即可5阶汉诺塔从X盘移到Z盘

递归操作仔细想想就可以了，这样栈的操作逐渐明朗，你就可以用汇编语言实现它了（通过bp栈指针的运算进栈push出栈pop就可以实现相应递归调用）。

汇编代码实现如下：

 DATA    SEGMENT
         n db ?
         msg db 0dh,0ah,'Enter the number you want : $'
         msg1 db 0dh,0ah,'HANOI-MOVE Procedure with : $',0ah,0dh
         to db '--->$'
         count dw    ; 5个一组输出显示
 DATA    ENDS

 CODE    SEGMENT
         ASSUME CS:CODE,DS:DATA
 START:
         MOV     AX,DATA
         MOV     DS,AX

         LEA DX,msg
         CALL intro
 KEYIN:
         MOV AH,01H         ;字符输入并回显
         INT 21H
         MOV byte ptr[n],Al         ;接收键入的n值

         LEA DX,msg1
         CALL intro
         MOV DL,0ah
         CALL DISPLAY

         MOV AL,byte ptr[n]
         SUB AL,30H
         CBW
         MOV DX,AX
         MOV AX,'X'
         MOV BX,'Y'
         MOV CX,'Z'
         ;MOV DX,[n]

         PUSH DX
         PUSH CX
         PUSH BX
         PUSH AX

         CALL HANOI_MOVE
         ADD SP,

         MOV DL,0ah
         CALL DISPLAY
         LEA DX,msg
         CALL intro
         JMP KEYIN

 GroupMake:
         INC [count]
         MOV AX,[count]
         MOV BL,           ;5 个一组
         DIV BL
         CMP AH,
         JNE SPACE
         MOV DL,0ah
         CALL DISPLAY        ;输出换行
         JMP CLOSE
     SPACE:
         MOV DX,20H
         CALL DISPLAY        ;输出空格
     CLOSE:
           RET

 STEP:     ;输出步骤号
         MOV AX,[count]  ;防止count多位数不正确输出--hexTOdec
         MOV CX,
         MOV BX,
 DISP1:
         MOV DX,
         DIV BX
         PUSH DX
         INC CX
         OR AX,AX
         JNZ DISP1    

         MOV DL,5BH    ; 输出显示[
         CALL DISPLAY
 DISP2:
         POP DX
         ADD DL,30H    ; 输出显示对应十进制
         CALL DISPLAY
         LOOP DISP2   

         MOV DL,5DH    ; 输出显示]
         CALL DISPLAY
         RET        

 intro proc near          ;提示语
          MOV AH,09H
          INT 21H
          ret
 intro endp

 DISPLAY proc near        ;输出字符
         MOV AH,02H
         INT 21H
         RET
 DISPLAY endp

 HANOI_MOVE proc near
         MOV BP,SP
         MOV AX,[BP+]
         CMP AX,
         JG moreThanOne    ;n 不等于1则跳转
         CALL STEP
         MOV DX,[BP+]     ;取第一个值
         CALL DISPLAY
         LEA DX,to
         CALL intro
         MOV DX,[BP+]     ;取第三个值
         CALL DISPLAY
         CALL GroupMake

           RET

 moreThanOne:
         MOV AX,[BP+]
         MOV BX,[BP+]
         MOV CX,[BP+]
         MOV DX,[BP+]
         DEC DX              ;n-1
         PUSH DX
         PUSH BX
         PUSH CX
         PUSH AX
         CALL HANOI_MOVE      ;递归一次，进行下一循环
         ADD SP,

         MOV BP,SP
         CALL STEP
         MOV DX,[BP+]     ;取第一个值
         CALL DISPLAY
         LEA DX,to
         CALL intro
         MOV DX,[BP+]     ;取第三个值
         CALL DISPLAY
         CALL GroupMake

         MOV AX,[BP+]
         MOV BX,[BP+]
         MOV CX,[BP+]
         MOV DX,[BP+]
         DEC DX              ;n-1
         PUSH DX
         PUSH CX
         PUSH AX
         PUSH BX
         CALL HANOI_MOVE      ;递归一次，进行下一循环
         ADD SP,

         RET
 HANOI_MOVE endp

 EXIT:   MOV     AH,4CH      ;退出系统
         INT    21H
 CODE    ENDS
         END START

耐心看看就行了，不是很难，栈的第一个参数是从bp+2开始的，别搞错了。
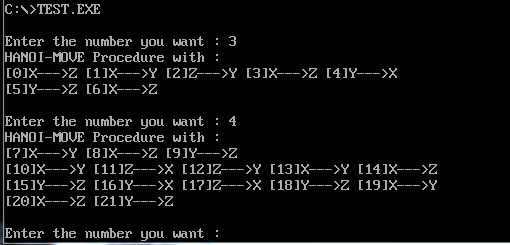
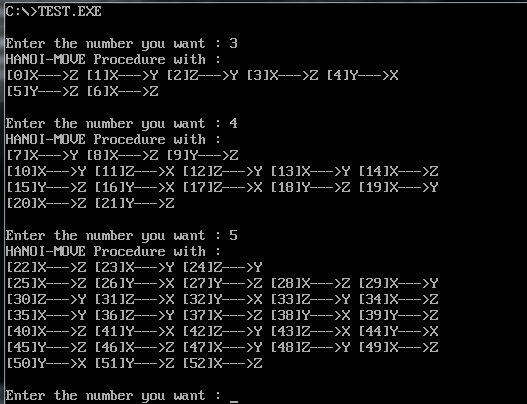
此为MASM语言格式汇编程序，链接成功后生成相应exe文件，打开即有如下执行效果..

============================此为原创文章，转载请注明。谢谢。======================================