0 前言

声明：此篇博客仅用于个人学习记录之用，并非是分享代码。Hornor the Code

我只能说，衣料模拟的技术深度比3D刚体模拟的技术深太多了。这次的实验参考了许多资料，包括

  • 《University of Tennessee MES301 Fall, 2023》
  • 《Root finding and optimization: Scientific Computing for Physicists 2017》
  • 《Physics-based animation lecture 5: OH NO! It's More Finite Elements》 这个老师讲课用一个小猫，特逗
  • 当然主要还是 Games103王华民老师的《Intro to Physics-Based Animation!》

里面用到的一些技术，在有限元里也有应用。

另外还有不基于物理的衣料模拟 《Position Based Dynamics》, 这个是05年左右开始出现的技术。详细的内容可以看PBA 2014: Position Based Dynamics by Ladislav Kavan，因为不基于物理，这里不再涉及。

1 Implicit Method

\[\begin{cases}\mathbf{v}^{[1]}=\mathbf{v}^{[0]}+\Delta t\mathbf{M}^{-1}\mathbf{f}^{[1]}\\\\\mathbf{x}^{[1]}=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[1]}\end{cases}
\]

进行一些简单的变换。

\[\left.\left\{\begin{array}{l}\mathbf{x}^{[1]}=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}+\Delta t^2\mathbf{M}^{-1}\mathbf{f}^{[1]}\\\\\mathbf{v}^{[1]}=(\mathbf{x}^{[1]}-\mathbf{x}^{[0]})/\Delta t\end{array}\right.\right.
\]

这里，我们只是认为力是位置的函数，所以可以写成。

\[\mathbf{x}^{[1]}=\mathbf{x}^{[0]}+\Delta t\mathbf{v}^{[0]}+\Delta t^2\mathbf{M}^{-1}\mathbf{f}(\mathbf{x}^{[1]})
\]

这就需要解一个非线性方程，其中力并非是线性的。

In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input.

In mathematics, a linear map (or linear function) \(f(x)\) is one which satisfies both of the following properties:

\[\bullet\text{ Homogeneity: }f(\alpha x)=\alpha f(x).
\]
\[\bullet\text{Additivity or superposition principle:}f(x+y)=f(x)+f(y);
\]

wikipedia : Nonlinear_system

\[\mathbf{x}^{[1]}=\operatorname{argmin}F(\mathbf{x})\quad\mathrm{~for~}\quad F(\mathbf{x})=\frac1{2\Delta t^2}\|\mathbf{x}-\mathbf{x}^{[0]}-\Delta t\mathbf{v}^{[0]}\|_{\mathbf{M}}^2+E(\mathbf{x})
\]
\[\|\mathbf{x}\|_{\mathbf{M}}^2=\mathbf{x}^{\mathrm{T}}\mathbf{M}\mathbf{x}
\]

上面的式子其实是求出了隐式积分的原函数，上式求导就是隐式积分本身。

\[\begin{aligned}\nabla F&\left(\mathbf{x}^{[1]}\right)=\frac1{\Delta t^2}\mathbf{M}\left(\mathbf{x}^{[1]}-\mathbf{x}^{[0]}-\Delta t\mathbf{v}^{[0]}\right)-\mathbf{f}\left(\mathbf{x}^{[1]}\right)=\mathbf{0}\\\\&\mathbf{x}^{[1]}-\mathbf{x}^{[0]}-\Delta t\mathbf{v}^{[0]}-\Delta t^2\mathbf{M}^{-1}\mathbf{f}\left(\mathbf{x}^{[1]}\right)=\mathbf{0}\end{aligned}
\]

所以一个求解非线性方程，或者是求解非线性方程根的模式就可以变成优化问题，而且是非线性优化。

1.1 Root-finding

The solution of nonlinear algebraic equations is frequently called root-finding, since our goal is to find the value of \(x\) such that $$f(x) = 0.$$

1.2 Optimization

Optimization means finding a maximum or minimum.

In mathematical terms, optimization means finding where the derivative is zero.

\[\frac{df(x)}{dx}=0.
\]

University of Tennessee MES301

Root finding and optimization: Scientific Computing for Physicists 2017

1.3 Insight

我们看到，这两个东西很像，基本就是解方程。所以有时候我们可以将其进行转化。

就是导数和积分的关系。

Physics-based animation lecture 5: OH NO! It's More Finite Elements

2 Newton-Raphson Method

Given a current \(\mathbf{x}^{(k)}\), we approximate our goal by:

\[\nabla F(\mathbf{x})\approx\nabla F\big(\mathbf{x}^{(k)}\big)+\frac{\partial F^2\big(\mathbf{x}^{(k)}\big)}{\partial\mathbf{x}^2}\big(\mathbf{x}-\mathbf{x}^{(k)}\big)=\mathbf{0}
\]

We then solve:

\[\frac{\partial F^2\big(\mathbf{x}^{(k)}\big)}{\partial\mathbf{x}^2}\Delta\mathbf{x}=-\nabla F\big(\mathbf{x}^{(k)}\big)
\]
\[\mathbf{x}^{(k+1)}\leftarrow\mathbf{x}^{(k)}+\Delta\mathbf{x}
\]

Specifically to simulation, we have:

\[\begin{gathered}
F(\mathbf{x})=\frac1{2\Delta t^2}\|\mathbf{x}-\mathbf{x}^{[0]}-\Delta t\mathbf{v}^{[0]}\|_{\mathbf{M}}^2+E(\mathbf{x}) \\
\nabla F\left(\mathbf{x}^{(k)}\right)=\frac1{\Delta t^2}\mathbf{M}\left(\mathbf{x}^{(k)}-\mathbf{x}^{[0]}-\Delta t\mathbf{v}^{[0]}\right)-\mathbf{f}\left(\mathbf{x}^{(k)}\right)\\
\frac{\partial F^2\left(\mathbf{x}^{(k)}\right)}{\partial\mathbf{x}^2}=\frac1{\Delta t^2}\mathbf{M}+\mathbf{H}(\mathbf{x}^{(k)})
\end{gathered}
\]

3 Mass-Spring System

\[\frac{\partial\|\mathbf{x}\|}{\partial\mathbf{x}}=\frac{\partial\left(\mathbf{x}^\mathrm{T}\mathbf{x}\right)^{1/2}}{\partial\mathbf{x}}=\frac{1}{2}\left(\mathbf{x}^\mathrm{T}\mathbf{x}\right)^{-1/2}\frac{\partial\left(\mathbf{x}^\mathrm{T}\mathbf{x}\right)}{\partial\mathbf{x}}=\frac{1}{2\|\mathbf{x}\|}2\mathbf{x}^\mathrm{T}=\frac{\mathbf{x}^\mathrm{T}}{\|\mathbf{x}\|}
\]
\[\frac{\partial\left(\mathbf{x}^\mathrm{T}\mathbf{x}\right)}{\partial\mathbf{x}}
\]

3.1 Matrix calculus

\[\mathbf u=\mathbf u(\mathbf x),\mathbf v=\mathbf v(\mathbf x)
\]
\[\frac{\partial(\mathbf{u}\cdot\mathbf{v})}{\partial\mathbf{x}}=\frac{\partial\mathbf{u}^\top\mathbf{v}}{\partial\mathbf{x}} = \mathbf{u}^{\top}{\frac{\partial\mathbf{v}}{\partial\mathbf{x}}}+\mathbf{v}^{\top}{\frac{\partial\mathbf{u}}{\partial\mathbf{x}}}
\]
\[\frac{\partial \mathbf{x}}{\partial \mathbf{x}}=\mathbb{I}
\]
\[\frac{\partial\mathbf{u}}{\partial\mathbf{x}},\frac{\partial\mathbf{v}}{\partial\mathbf{x}}\text{in numerator layout}
\]

3.2 A Spring with Two Ends

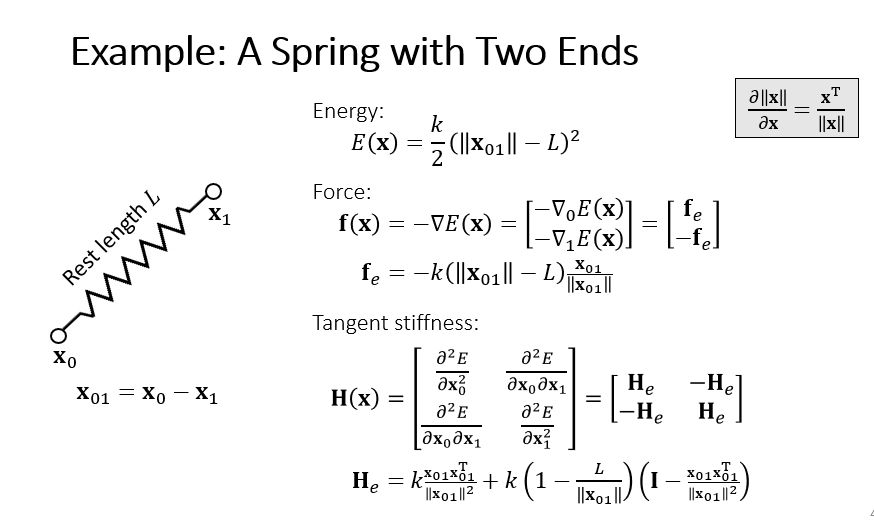
图片来源：Games103

4 Explaination of Init Code with 3D Image

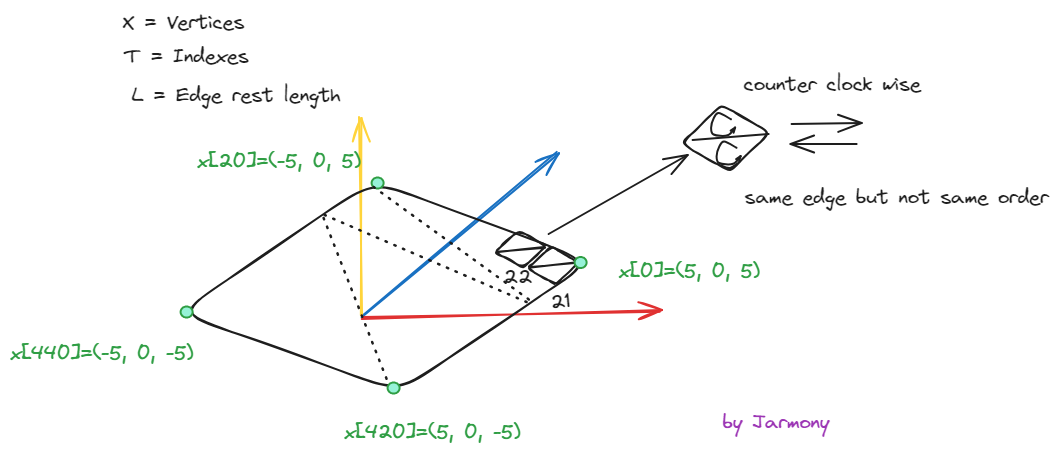
4.1 Initialize

  1. void Start()
  2. {
  3. 	Mesh mesh = GetComponent<MeshFilter> ().mesh;
  5. 	//Resize the mesh.
  6. 	int n=21;
  7. 	Vector3[] X  	= new Vector3[n*n];
  8. 	Vector2[] UV 	= new Vector2[n*n];
  9. 	int[] triangles	= new int[(n-1)*(n-1)*6];
  10. 	for(int j=0; j<n; j++)
  11. 		for(int i=0; i<n; i++)
  12. 		{
  13. 			X[j*n+i] =new Vector3(5-10.0f*i/(n-1), 0, 5-10.0f*j/(n-1));
  14. 			UV[j*n+i]=new Vector3(i/(n-1.0f), j/(n-1.0f));
  15. 		}
  16. 	int t=0;
  17. 	for(int j=0; j<n-1; j++)
  18. 		for(int i=0; i<n-1; i++)
  19. 		{
  20. 			triangles[t*6+0]=j*n+i;
  21. 			triangles[t*6+1]=j*n+i+1;
  22. 			triangles[t*6+2]=(j+1)*n+i+1;
  23. 			triangles[t*6+3]=j*n+i;
  24. 			triangles[t*6+4]=(j+1)*n+i+1;
  25. 			triangles[t*6+5]=(j+1)*n+i;
  26. 			t++;
  27. 		}
  28. 	mesh.vertices=X;
  29. 	mesh.triangles=triangles;
  30. 	mesh.uv = UV;
  31. 	mesh.RecalculateNormals ();
  33. 	Debug.Log("triangles.Length " + triangles.Length);
  35. 	//Construct the original E
  36. 	int[] _E = new int[triangles.Length*2];
  38. 	Debug.Log("_E.Length " + _E.Length);
  39. 	for (int i=0; i<triangles.Length; i+=3)
  40. 	{
  41. 		_E[i*2+0]=triangles[i+0];
  42. 		_E[i*2+1]=triangles[i+1];
  43. 		_E[i*2+2]=triangles[i+1];
  44. 		_E[i*2+3]=triangles[i+2];
  45. 		_E[i*2+4]=triangles[i+2];
  46. 		_E[i*2+5]=triangles[i+0];
  47. 	}
  48. 	//Reorder the original edge list
  49. 	for (int i=0; i<_E.Length; i+=2)
  50. 		if(_E[i] > _E[i + 1])
  51. 			Swap(ref _E[i], ref _E[i+1]);
  52. 	//Sort the original edge list using quicksort
  53. 	// One edge have two end point, this quicksort method sort all of them at the same time
  54. 	// the order is from small to big with the pattern of
  55. 	// [start end] [start end] [start end]
  57. 	//Debug.Log("_E.Length/2-1 " + (_E.Length / 2 - 1) );
  58. 	Quick_Sort(ref _E, 0, _E.Length/2-1);
  60. 	// short-circuit evaluation: or(if first condition is true then skip other) and(if first condition is false then skip other)
  61. 	int e_number = 0;
  62. 	for (int i=0; i<_E.Length; i+=2)
  63. 		if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
  64. 			e_number++;
  66. 	E = new int[e_number * 2];
  67. 	for (int i=0, e=0; i<_E.Length; i+=2)
  68. 		if (i == 0 || _E [i + 0] != _E [i - 2] || _E [i + 1] != _E [i - 1])
  69. 		{
  70. 			E[e*2+0]=_E [i + 0];
  71. 			E[e*2+1]=_E [i + 1];
  72. 			e++;
  73. 		}
  75. 	// [0-9] 10/2=5 <5=4 4*2+1=9
  76. 	// [0-10] 11/2=5 <5=4 4*2+1=9
  77. 	// asert(E.length % 2 == 0) this should always be true, becuase we use one dim array to store the Edges. One edge takes two places in this array.
  78. 	L = new float[E.Length/2];
  79. 	for (int e=0; e<E.Length/2; e++)
  80. 	{
  81. 		int v0 = E[e*2+0];
  82. 		int v1 = E[e*2+1];
  83. 		L[e]=(X[v0]-X[v1]).magnitude;
  84. 	}
  86. 	V = new Vector3[X.Length];
  87. 	for (int i=0; i<V.Length; i++)
  88. 		V[i] = new Vector3 (0, 0, 0);
  89. }

4.2 Index

  1. int t=0;
  2. // Because of 21 points have 20 gaps, this index will iterate 400 squares and split them two triangels
  3. // per square.
  4. for(int j=0; j<n-1; j++)
  5. for(int i=0; i<n-1; i++)
  6. {
  7. 	triangles[t*6+0]=j*n+i;
  8. 	triangles[t*6+1]=j*n+i+1;
  9. 	triangles[t*6+2]=(j+1)*n+i+1;
  10. 	triangles[t*6+3]=j*n+i;
  11. 	triangles[t*6+4]=(j+1)*n+i+1;
  12. 	triangles[t*6+5]=(j+1)*n+i;
  13. 	t++;
  14. }

这里的 triangles 其实就是 三角形顶点的Index(下标)。

  1. State: j=0, i=0, t=0.
  2. t[0] = 0
  3. t[1] = 1
  4. t[2] = 22
  5. t[3] = 0
  6. t[4] = 22
  7. t[5] = 21
  9. /*********/
  11. State: j=0, i=1, t=1.
  12. t[6] = 1
  13. t[7] = 2
  14. t[8] = 23
  15. t[9] = 1
  16. t[10] = 23
  17. t[11] = 22

4.3 Edge

  1. //Construct the original E
  2. int[] _E = new int[triangles.Length*2];
  4. Debug.Log("_E.Length " + _E.Length);
  5. for (int i=0; i<triangles.Length; i+=3)
  6. {
  7. 	_E[i*2+0]=triangles[i+0];
  8. 	_E[i*2+1]=triangles[i+1];
  10. 	_E[i*2+2]=triangles[i+1];
  11. 	_E[i*2+3]=triangles[i+2];
  13. 	_E[i*2+4]=triangles[i+2];
  14. 	_E[i*2+5]=triangles[i+0];
  15. }
  16. //Reorder the original edge list
  17. for (int i=0; i<_E.Length; i+=2)
  18. 	if(_E[i] > _E[i + 1])
  19. 		Swap(ref _E[i], ref _E[i+1]);

因为这里使用一维数组进行边的存储，那么从一条边到另一条边的步长是2。

  1. State: i=0.
  2. _E[0] = t[0]:0
  3. _E[1] = t[1]:1
  4. _E[2] = t[1]:1
  5. _E[3] = t[2]:22
  6. _E[4] = t[2]:22
  7. _E[5] = t[0]:0
  9. /*********/
  11. State: i=3.
  12. _E[6]= t[3]:0
  13. _E[7] = t[4]:22
  14. _E[8] = t[4]:22
  15. _E[9] = t[5]:21
  16. _E[10] = t[5]:21
  17. _E[11] = t[3]:0

4.4 Sort Edge

  1. //Reorder the original edge list
  2. 	for (int i=0; i<_E.Length; i+=2)
  3. 		if(_E[i] > _E[i + 1])
  4. 			Swap(ref _E[i], ref _E[i+1]);

初始的时候，一条边有两种表达方式。我们将其都按从小的顶点到大的顶点进行重新排序，一条边就只有一种表达方式。

  1. Quick_Sort(ref _E, 0, _E.Length/2-1);
  3. void Quick_Sort(ref int[] a, int l, int r)
  4. {
  5. 	int j;
  6. 	if(l<r)
  7. 	{
  8. 		j=Quick_Sort_Partition(ref a, l, r);
  9. 		Quick_Sort (ref a, l, j-1);
  10. 		Quick_Sort (ref a, j+1, r);
  11. 	}
  12. }
  14. int  Quick_Sort_Partition(ref int[] a, int l, int r)
  15. {
  16. 	int pivot_0, pivot_1, i, j;
  17. 	pivot_0 = a [l * 2 + 0];
  18. 	pivot_1 = a [l * 2 + 1];
  19. 	i = l;
  20. 	j = r + 1;
  21. 	//Debug.Log("i: " + i + " j:" + j);
  22. 	while (true)
  23. 	{
  24. 		do ++i; while( i<=r && (a[i*2]<pivot_0 || a[i*2]==pivot_0 && a[i*2+1]<=pivot_1));
  25. 		do --j; while(  a[j*2]>pivot_0 || a[j*2]==pivot_0 && a[j*2+1]> pivot_1);
  26. 		if(i>=j)	break;
  27. 		Swap(ref a[i*2], ref a[j*2]);
  28. 		Swap(ref a[i*2+1], ref a[j*2+1]);
  29. 	}
  30. 	Swap (ref a [l * 2 + 0], ref a [j * 2 + 0]);
  31. 	Swap (ref a [l * 2 + 1], ref a [j * 2 + 1]);
  32. 	return j;
  33. }
  35. void Swap(ref int a, ref int b)
  36. {
  37. 	int temp = a;
  38. 	a = b;
  39. 	b = temp;
  40. }

这里的quick sort是以两个数为一次比较的依据，好像是这两个数打包(其实就是一条边)进行比较，平常就是一次比较只关心一个数。

5 Update

  1. // Update is called once per frame
  2. void Update ()
  3. {
  4. 	Mesh mesh = GetComponent<MeshFilter> ().mesh;
  5. 	Vector3[] X 		= mesh.vertices;
  6. 	Vector3[] last_X 	= new Vector3[X.Length];
  7. 	Vector3[] X_hat 	= new Vector3[X.Length];
  8. 	Vector3[] G 		= new Vector3[X.Length];
  10. 	//Initial Setup.
  11. 	for (int i = 0; i < X.Length; i++)
  12. 	{
  13.         if (i == 0 || i == 20) continue;
  14.         V[i] = V[i] * damping;
  15. 		X_hat[i] = X[i] + V[i] * t;
  16. 		last_X[i] = X[i];
  18. 		// Guess X[i] init state
  19. 		X[i] = X_hat[i];
  20.     }
  22.     float invSquareDt = 1 / (t * t);
  23. 	// Hessian Matrix is complicated to construct
  24. 	// So we use some fake inverse, due to the mass is same for all vertices, we put this out of the loop.
  25.     float fakeInv = 1 / (invSquareDt * mass + 4.0f * spring_k);
  26.     for (int k=0; k<32; k++)
  27. 	{
  28. 		Get_Gradient(X, X_hat, t, G);
  30.         //Update X by gradient.
  32.         for (int i = 0; i < X.Length; i++)
  33.         {
  34.             if (i == 0 || i == 20) continue;
  35.             X[i] = X[i] - fakeInv * G[i];
  36.         }
  38.     }
  40. 	float invTime = 1.0f / t;
  41.     for (int i = 0; i < X.Length; i++)
  42.     {
  43.         if (i == 0 || i == 20) continue;
  44.         V[i] = invTime * (X[i] - last_X[i]);
  45.     }
  47.     //Finishing.
  49.     mesh.vertices = X;
  51. 	Collision_Handling ();
  52. 	mesh.RecalculateNormals ();
  53. }

因为要进行优化，位置迭代，来找到最小值。所以需要一个迭代的初始位置，设置为X_init = X[i] + V[i] * t。也可以不设置，不进行变化。

6 Get_Gradient

  1. void Get_Gradient(Vector3[] X, Vector3[] X_hat, float t, Vector3[] G)
  2. {
  3. 	//Momentum and Gravity.
  4. 	float invSquareDt = 1 / (t * t);
  5. 	for (int i = 0; i < X.Length; i++)
  6. 	{
  7. 		G[i] = invSquareDt * mass * (X[i] - X_hat[i]) - mass * gravity;
  8.     }
  10. 	//Spring Force.
  11. 	Vector3 spForceDir = Vector3.zero;
  12. 	Vector3 spForce = Vector3.zero;
  14.     for (int e = 0; e < E.Length / 2; e++)
  15. 	{
  16.         int vi = E[e * 2 + 0];
  17.         int vj = E[e * 2 + 1];
  19.         spForceDir = X[vi] - X[vj];
  20. 		spForce = spring_k * (1.0f - L[e] / spForceDir.magnitude) * spForceDir;
  21. 		G[vi] = G[vi] + spForce;
  22. 		G[vj] = G[vj] - spForce;
  23.     }
  24. }

6.1 first derivative

\[\mathbf{g}=\frac{1}{\Delta t^2}\mathbf{M}(\mathbf{x}-\tilde{\mathbf{x}})-\mathbf{f}(\mathbf{x}),
\]

由于上式的特性，我们需要两次遍历来得到梯度一阶导的数值。

  • 逐顶点
\[\mathbf{g}_{i}\leftarrow\frac{1}{\Delta t^{2}}\mathbf{m}_{i}(\mathbf{x}_{i}-\tilde{\mathbf{x}}_{i}).
\]
  • 逐边计算弹簧弹力
\[\left.\left\{\begin{array}{l}\mathbf{g}_i\leftarrow\mathbf{g}_i+k(1-\frac{L_e}{\|\mathbf{x}_i-\mathbf{x}_j\|})(\mathbf{x}_i-\mathbf{x}_j)\\\mathbf{g}_j\leftarrow\mathbf{g}_j-k(1-\frac{L_e}{\|\mathbf{x}_i-\mathbf{x}_j\|})(\mathbf{x}_i-\mathbf{x}_j)\end{array}\right.\right..
\]

当然无论是逐顶点还是逐边，导数都是位置的函数。

最后给每一个顶点的梯度加上重力，当然根据 g 需要加负号。

6.2 second derivative

In reality, there are two roadblocks:

1)The Hessian matrix is complicated to construct;

2) the linear solver is difficult to implement on Unity.

Instead, we choose a much simpler method by considering the Hessian as a diagonal matrix. This

yields a simple update to every vertex as:

\[\mathbf{x}_{i}\leftarrow\mathbf{x}_{i}-\left(\frac{1}{\Delta t^{2}}m_{i}+4k\right)^{-1}\mathbf{g}_{i}.
\]

Games103 Huamin Wang Lab2

7 Collision_Handling

  1. void Collision_Handling()
  2. {
  3. 	Mesh mesh = GetComponent<MeshFilter> ().mesh;
  4. 	Vector3[] X = mesh.vertices;
  6. 	//Handle colllision.
  7. 	Vector3 ballPos = GameObject.Find("Sphere").transform.position;
  8. 	float radius = 2.7f;
  10. 	for (int i = 0; i < X.Length; i++)
  11. 	{
  12. 		if (i == 0 || i == 20) continue;
  13. 		if (SDF(X[i], ballPos))
  14. 		{
  15. 			V[i] = V[i] + 1.0f / t * (ballPos + radius * (X[i] - ballPos).normalized - X[i]);
  16. 			X[i] = ballPos + radius * (X[i] - ballPos).normalized;
  17. 		}
  18. 	}
  19. }
  21. bool SDF(Vector3 v, Vector3 center, float radius = 2.7f)
  22. {
  24. 	float sdf = (v - center).magnitude - radius;
  25. 	return sdf > 0.0f ? false : true;
  26. }

Once a colliding vertex is found, apply impulse-based method as follows:

\[\mathbf{v}_i\leftarrow\mathbf{v}_i+\frac{1}{\Delta t}\left(\mathbf{c}+r\frac{\mathbf{x}_i-\mathbf{c}}{\|\mathbf{x}_i-\mathbf{c}\|}-\mathbf{x}_i\right),\quad\mathbf{x}_i\leftarrow\mathbf{c}+r\frac{\mathbf{x}_i-\mathbf{c}}{\|\mathbf{x}_i-\mathbf{c}\|}.
\]

图片来源：Games103

Cloth Simulation with Root Finding and Optimization的更多相关文章

  1. [zz] Pixar’s OpenSubdiv V2: A detailed look

    http://www.fxguide.com/featured/pixars-opensubdiv-v2-a-detailed-look/ Pixar’s OpenSubdiv V2: A detai ...

  2. My Open Source Projects

    • MyMagicBox (https://github.com/yaoyansi/mymagicbox)   Role: Creator   Miscellaneous projects for e ...

  3. Computer Graphics Research Software

    Computer Graphics Research Software Helping you avoid re-inventing the wheel since 2009! Last update ...

  4. Matlab 中S-函数的使用 sfuntmpl

    function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag) %SFUNTMPL General MATLAB S-Functi ...

  5. Optimizing graphics performance

    看U3D文档,心得:对于3D场景,使用分层次的距离裁剪,小物件分到一个层,稍远时就被裁掉,大物体分到一个层,距离很远时才裁掉,甚至不载.中物体介于二者之间. 文档如下: Good performanc ...

  6. Code Project精彩系列（转）

    Code Project精彩系列(转)   Code Project精彩系列(转)   Applications Crafting a C# forms Editor From scratch htt ...

  7. 万字教你如何用 Python 实现线性规划

    摘要:线性规划是一组数学和计算工具,可让您找到该系统的特定解,该解对应于某些其他线性函数的最大值或最小值. 本文分享自华为云社区<实践线性规划:使用 Python 进行优化>,作者: Yu ...

  8. Position Based Dynamics【译】

    绝大部分机翻,少部分手动矫正,仅供参考.本人水平有限,如有误翻,概不负责... Position Based Dynamics Abstract The most popular approaches ...

  9. 网格弹簧质点系统模拟（Spring-Mass System by Euler Integration）

    弹簧质点模型是利用牛顿运动定律来模拟物体变形的方法.如下图所示,该模型是一个由m×n个虚拟质点组成的网格,质点之间用无质量的.自然长度不为零的弹簧连接.其连接关系有以下三种: 1.连接质点[i, j] ...

  10. 编写更少量的代码：使用apache commons工具类库

    Commons-configuration   Commons-FileUpload   Commons DbUtils   Commons BeanUtils  Commons CLI  Commo ...

随机推荐

  1. Linux系统下使用pytorch多进程读取图片数据时的注意事项——DataLoader的多进程使用注意事项

    原文: PEP 703 – Making the Global Interpreter Lock Optional in CPython 相关内容: The GIL Affects Python Li ...

  2. 说说中国高校理工科教育中的基础概念混乱问题——GPU是ASIC吗

    在YouTube上看到这样一个视频: https://www.youtube.com/watch?v=7EXDp6c9n-Q&lc=Ugydwl8gppB5FWE8Y5V4AaABAg.9fc ...

  3. CH04_程序流程结构

    CH04_程序流程结构 程序流程结构 C/C++支持最基本的三种程序运行结构: 顺序结构:程序按顺序执行,不发生挑战 选择结构:依据条件是否满足,有选择的执行相应的功能 循环结构:依据条件是否满足,循 ...

  4. 5 个有趣的 Python 开源项目「GitHub 热点速览」

    本期,我从上周的开源热搜项目中精心挑选了 5 个有趣.好玩的 Python 开源项目. 首先是 PyScript,它可以让你直接在浏览器中运行 Python 代码,不仅支持在 HTML 中嵌入,还能安 ...

  5. 金融、支付行业的开发者不得不知道的float、double计算误差问题

    为什么浮点数 float 或 double 运算的时候会有精度丢失的风险呢? <阿里巴巴 Java 开发手册>中提到:"浮点数之间的等值判断,基本数据类型不能用 == 来比较,包 ...

  6. Tesla 开发者 API 指南：BLE 密钥 – 身份验证和车辆命令

    注意:本工具只能运行于 mac 或者 linux, win下不支持. 1. 克隆项目到本地 https://github.com/teslamotors/vehicle-command.git 2. ...

  7. mysql外键设置失败踩坑记录

    把表里面的数据清空再添加 原因 因为外键一定要对应外面那个表的数据,现在添加外键会导致这个外键的值为空,违反了键的非空约定 理解为已有的数据突然多出来个字段,但是不知道值是什么,那就为空了 主键和外键 ...

  8. Linux 常见编辑器

    命令行编辑器 Vim Linux 上最出名的编辑器当属 Vim 了.Vim 由 Vi 发展而来,Vim 的名字意指 Vi IMproved,表示 Vi 的升级版.Vim 对于新手来说使用比较复杂,不过 ...

  9. [深度学习] 时间序列分析工具TSLiB库使用指北

    TSLiB是一个为深度学习时间序列分析量身打造的开源仓库.它提供了多种深度时间序列模型的统一实现,方便研究人员评估现有模型或开发定制模型.TSLiB涵盖了长时预测(Long-term forecast ...

  10. webpack系列-externals配置使用（CDN方式引入JS）

    如果需要引用一个库,但是又不想让webpack打包(减少打包的时间),并且又不影响我们在程序中以CMD.AMD或者window/global全局等方式进行使用(一般都以import方式引用使用),那就 ...