POJ 2409 Let it Bead（polya裸题）

题目传送：http://poj.org/problem?id=2409

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

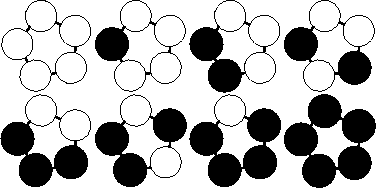For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0

Sample Output

1
2
3
5
8
13
21

启发博客：http://blog.csdn.net/sr_19930829/article/details/38108871

polya定理看的我好累。。总算是在理解的基础上敲出一道裸题

关键就是在循环节个数和长度以及置换群个数的理解上

1.旋转。

环每次顺时针如果旋转i格，那么每循环lcm(n,i)个可以回到原来的状态。

每次旋转i个，所以循环节长度为lcm(n,i)/i。

由此推出循环节个数为n/(lcm(n,i)/i)即gcd(n,i)。

由polya定理可得染色方案为 ∑c^gcd(n,i) 其中 i=1,2,3,4,....n，置换群个数有n个

2.翻转。

这里得考虑两种情况，循环节长度为3，即珠子本身和翻转对应的那一颗。置换群个数有n个。

当n为奇数时，共有n个循环节个数为（n/2+1)的循环群，染色方案为 n*c^(n/2+1)

当n为偶数时，共有n个循环群，其中有n/2个的循环节个数为（n/2 +1)， 有n/2个的循环节个数为（n/2)。 染色方案分别为 (n/2)*c^(n/2+1)以及(n/2)*c^(n/2)。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<string>
 #include<cmath>
 using namespace std;

 long long gcd(long long b,long long c)//计算最大公约数
 {
 return c==?b:gcd(c,b%c);
 }

 long long quick_mod(long long a,long long b)//快速幂，复杂度log2n
 {
     long long ans=;
     while(b)
     {
         if(b&)
         {
             ans=(ans*a);
             b--;
         }
         b/=;
         a=a*a;
     }
     return ans;
 }

 int main()
 {
     int c,s;
     long long res;
     while(~scanf("%d%d",&c,&s)&&(c+s))
     {
         res=;
         //翻转
         for(int i=;i<=s;i++)
             res+=quick_mod(c,gcd(s,i));
         //旋转
         if(s%!=)
             res+=s*quick_mod(c,s/+);
         else
             res+=s/*quick_mod(c,s/+)+s/*quick_mod(c,s/);
         res/=*s;
         printf("%lld\n",res);
     }
     return ;
 }