kmeans笔记

1.算法过程

a.随机选取k个初始点作为中心点

b.依次计算剩余所有点分别与哪个初始点距离较近，则该点属于哪个簇

c.移动中心点到现在的簇的中心

d.重复b,c两步，直到中心点不再变化算法结束

2.优缺点

优点：容易实现

缺点：可能收敛到局部最小值，大规模数据集上收敛速度较慢

3.代码使用中出现的问题思考

调用sklearn中该模块：

k=8

kmeans = KMeans(n_clusters=k, random_state=0).fit(X)

也就是需要指定聚类个数，但是如何确定k值？有以下几种方法

a.最好有经验，通过经验指定

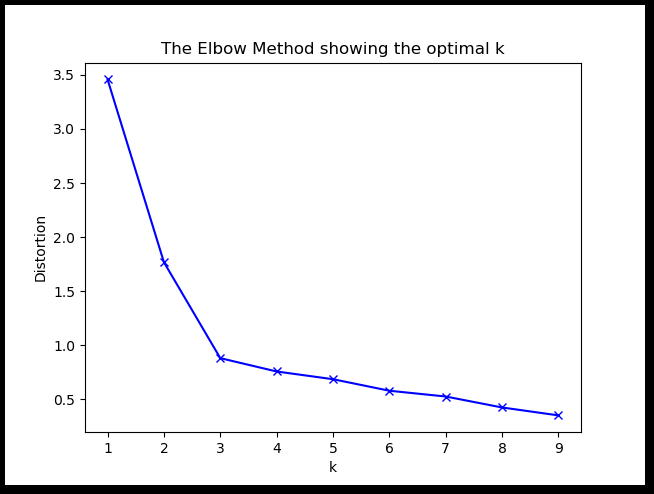
b.通过elbow method来确定，选取绘图结果k-elbow 直线拐点处对应的k值作为聚类个数。如下代码：

 # clustering dataset
# determine k using elbow method

from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
import numpy as np
import matplotlib.pyplot as plt

x1 = np.array([3, 1, 1, 2, 1, 6, 6, 6, 5, 6, 7, 8, 9, 8, 9, 9, 8])
x2 = np.array([5, 4, 5, 6, 5, 8, 6, 7, 6, 7, 1, 2, 1, 2, 3, 2, 3])

plt.plot()
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Dataset')
plt.scatter(x1, x2)
plt.show()

# create new plot and data
plt.plot()
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
colors = ['b', 'g', 'r']
markers = ['o', 'v', 's']

# k means determine k
distortions = []
K = range(1,10)
for k in K:
    kmeanModel = KMeans(n_clusters=k).fit(X)
    kmeanModel.fit(X)
    distortions.append(sum(np.min(cdist(X, kmeanModel.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0])

# Plot the elbow
plt.plot(K, distortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Distortion')
plt.title('The Elbow Method showing the optimal k')
plt.show()
如上图，取k值为3.

c.ISODATA算法针对这个问题进行了改进：当属于某个类别的样本数过少时把这个类别去除，当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别（类的自动合并和分裂）
d.还有以下几种方法，不过目前我没有理解其中的意义（2018.10.24）

• 根据方差分析理论，应用混合 F 统计量来确定最佳分类数，并应用了模糊划分熵来验证最佳分类数的正确性
• 使用了一种结合全协方差矩阵的 RPCL 算法，并逐步删除那些只包含少量训练数据的类（一种聚类算法）
• 使用的是一种称为次胜者受罚的竞争学习规则，来自动决定类的适当数目。它的思想是：对每个输入而言，不仅竞争获胜单元的权值被修正以适应输入值，而且对次胜单元采用惩罚的方法使之远离输入值。

4.噪声处理

k-means对离群值很敏感，，算法目标是簇内差异最小化，即SSE最小。

1.可以改用密度聚类，目标为类内距离最小，类间距离最大。

2.在假设目前聚类结果正确的前提下，通过计算p-value来决定聚类效果是否具有显著差异，去掉每个簇中的异常点。

（p-value指的是比较的两者的差别是由机遇所致的可能性大小。P值越小，越有理由认为对比事物间存在差异。例如，P<0.05,就是说结果显示的差别是由机遇所致的可能性不足5%，或者说，别人在同样的条件下重复同样的研究，得出相反结论的可能性不足5%。P>0.05称“不显著”；P<=0.05称“显著”，P<=0.01称“非常显著”）