[luogu4251 SCOI2015] 小凸玩矩阵 (二分图最大匹配)

传送门

Description

Input

Output

输出包含一行，为选出的 n 个数中第 k 大数的最小值。

Sample Input

输入样例1：

2 3 1

1 2 4

2 4 1

输入样例2：

3 4 2

1 5 6 6

8 3 4 3

6 8 6 3

Sample Output

输出样例1：

1

输出样例2：

3

HINT

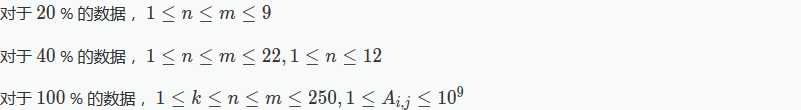
Solution

k大值最小，显然可以二分

对于mid若它是第k大数，则一定存在>=n-k-1个比mid小的数

用最大匹配的结果和n-k比较即可

Code

//By Menteur_Hxy
#include <vector>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define int long long
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
#define E(i,u) for(register int i=head[u];i;i=nxt[i])
#define ins(a,b,c) add(a,b,c),add(b,a,0)
#define add(a,b,c) nxt[++cnt]=head[a],to[cnt]=b,cst[cnt]=c,head[a]=cnt
using namespace std;

int read() {
	int x=0,f=1; char c=getchar();
	while(!isdigit(c)) {if(c=='-')f=-f;c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
	return x*f;
}

const int N=1010,INF=0x3f3f3f3f;
int n,m,k,ans,cnt,S,T;
int nxt[N*N],to[N*N],cst[N*N],head[N<<1],cur[N*N];
int da[N][N],dis[N<<1],que[N<<1];

bool bfs() {
	memset(dis,0,sizeof(dis));
	int h=0,t=1; que[++h]=S; dis[S]=1;
	while(h<=t) {
		int u=que[h++];
		// cout<<u<<" "<<dis[u]<<endl;
		E(i,u) if(!dis[to[i]]&&cst[i]>0)
			dis[to[i]]=dis[u]+1,que[++t]=to[i];
	}
	return dis[T]>0;
}

int dfs(int u,int flow) {
	if(u==T) return flow;
	int used=0;
	for(register int &i=cur[u],v;i;i=nxt[i])
		if(cst[i]>0&&dis[(v=to[i])]==dis[u]+1) {
			// cout<<u<<" "<<v<<endl;
			int tmp=dfs(v,min(flow-used,cst[i]));
			// cout<<min(flow-used,cst[i])<<" "<<tmp<<endl;
			cst[i]-=tmp; cst[i^1]+=tmp;
			used+=tmp; if(used==flow) return flow;
		}
	if(!used) dis[u]=-1;
	return used;
}

int dinic() {
	int res=0;
	while(bfs()) {
		// cout<<dis[T]<<endl;
		F(i,0,n+m+1) cur[i]=head[i];
		res+=dfs(S,INF);
	}
	return res;
}

bool jud(int x) {
	cnt=1;
	memset(head,0,sizeof(head));
	F(i,1,n) ins(S,i,1); F(i,1,m) ins(i+n,T,1);
	F(i,1,n) F(j,1,m) if(da[i][j]<=x) ins(i,j+n,1);
	int res=dinic();
	return res>n-k;
}

signed main() {
	// freopen("1.txt","r",stdin);
	n=read(),m=read(),k=read();
	S=0; T=n+m+1; ans=INF;
	int l=INF,r=0;
	F(i,1,n) F(j,1,m)
		da[i][j]=read(),l=min(l,da[i][j]),r=max(r,da[i][j]);
	while(l<=r) {
		int mid=(l+r)>>1;
		// cout<<mid<<endl;
		if(jud(mid)) ans=min(ans,mid),r=mid-1;
		else l=mid+1;
	}
	printf("%lld",ans);
	return 0;
}